4. Приближенные вычисления с помощью полного дифференциала.

Пусть функция f(x, y) дифференцируема в точке (х, у). Найдем полное приращение этой функции:

Если подставить в эту формулу выражение

то получим приближенную формулу:

Пример 4.1. Вычислить приближенно значение , исходя из значения функции при x = 1, y = 2, z = 1.

Из заданного выражения определим x = 1,04 – 1 = 0,04, y = 1,99 – 2 = -0,01,

z = 1,02 – 1 = 0,02.

Найдем значение функции u(x, y, z) =

Находим частные производные:

Полный дифференциал функции u равен:

Точное значение этого выражения: 1,049275225687319176.

5. Дифференцирование сложных функций и функций заданных неявно.

Если в функции аргументы и в свою очередь являются функциями аргумента , то по отношению к переменной функцию называют сложной. Производная такой функции находится по правилу

.

В функции аргументы могут быть также функциями двух переменных и . По отношению к переменным и функцию опять же называют сложной. Частные производные такой сложной функции находятся по правилам аналогичным доказанному выше

,

.

Пример 5.1.

Найти частную производную функции , если , .

Применяя известное правило, запишем

.

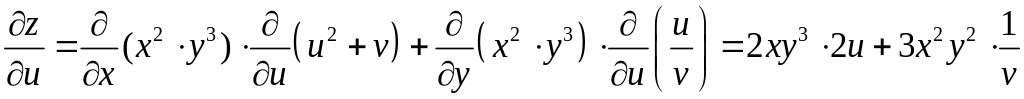При неявном задании функции одной переменной ее определяют из уравнения .

Не разрешая данное уравнение относительно , производную данной функции можно определить по правилу

.

Уравнение неявно определяет функцию двух переменных . Ее частные производные находятся по аналогичным формулам:

, .

Пример 5.2.

Найти функции, заданной неявно уравнением .

По правилу, указанному выше, имеем

.

6. Необходимое и достаточное условие экстремума.

Если для функции z = f(x, y), определенной в некоторой области, в некоторой окрестности точки М₀(х₀, у₀) верно неравенство

то точка М₀ называется точкой максимума.

Если для функции z = f(x, y), определенной в некоторой области, в некоторой окрестности точки М₀(х₀, у₀) верно неравенство

то точка М₀ называется точкой минимума.

Теорема. (Необходимые условия экстремума).

Если функция f(x,y) в точке (х₀, у₀) имеет экстремум, то в этой точке либо обе ее частные производные первого порядка равны нулю , либо хотя бы одна из них не существует.

Эту точку (х₀, у₀) будем называть критической точкой.

Теорема. (Достаточные условия экстремума).

Пусть в окрестности критической точки (х₀, у₀) функция f(x, y) имеет непрерывные частные производные до второго порядка включительно. Рассмотрим выражение:

1. Если D(x₀, y₀) > 0, то в точке (х₀, у₀) функция f(x, y) имеет экстремум, если

- максимум, если - минимум.

2. Если D(x₀, y₀) < 0, то в точке (х₀, у₀) функция f(x, y) не имеет экстремума

В случае, если D = 0, вывод о наличии экстремума сделать нельзя.

Пример 6.1. Исследовать функцию на экстремум.

Находим частные производные первого порядка и приравниваем их к нулю:

Стационарная точка данной функции имеет координаты .

Вычислим вторые производные .

Следовательно, .

Экстремум имеется, т.к. , то в точке - минимум, .

Пример 6.2. Исследовать функцию на экстремум.

Находим частные производные и приравниваем их к нулю

Стационарная точка данной функции имеет координаты .

Вычислим вторые производные: .

Следовательно, .

Экстремум отсутствует, т.к. .