Композиция линейных преобразований

Если к результату действия одного преобразования применить следующее, то в итоге можем получить преобразование более сложного характера. Понятно, что удобно рассуждать и наоборот.

Определение. Пусть заданы преобразования A: D→ G и  B : G→E.

Тогда преобразование C: D→ E, определяемое формулой C( f)=B( A(f)),  называют композицией преобразований B и A.

Композиция линейных преобразований – снова линейное преобразование. Действительно, из линейности A и B следует:

i) C( f + g ) = B( A( f)+ A(g )) = B( A( f) ) + B( A(g )) = C( f )+ C( g ),

ii) C(α * f) = B(α * A( f)) = α * B( A( f) ) = α *C( f).

Значит, композиция двух линейных преобразований также определяется матрицей. Эта матрица равна произведению матриц преобразований B и A (именно в таком порядке). Поэтому для отыскания матрицы композиции достаточно найти матрицы составляющих её преобразований.

Пример 9.

Задать аналитически преобразование, переводящее на плоскости фигуру D («уголок») в фигуру E (уменьшенный отражённый «уголок») (рис. 7).

Решение.

Искомое преобразование (обозначим его C) можно осуществить за два шага:

1) уменьшить фигуру D в два раза (сжать относительно начала координат)

– преобразование A,

2) сделать симметрию относительно оси Oy – преобразование B.

Таким образом, D переводится в E при помощи композиции преобразований B и A.

Рис. 7. Отображение фигур

A = 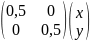, B = 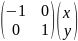. Следовательно,

C = B( A ) = * = .

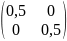
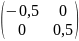Замечание. Очевидно, что в рассмотренной ситуации не было разницы в последовательности выполнения преобразований, имеет место:

B(A ) = A(B ). Но в общем случае это не так, поэтому и операция умножения матриц некоммутативна.

Рассмотрим, например, композицию поворота на угол 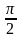- преобразование A, - и симметрии относительно прямой y = x - преобразование B.

Тогда B(A ) 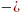симметрия относительно оси Ox, а A(B ) – симметрия относительно оси Oy. Действительно,

B*A = * = ,

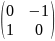A*B = * = .

Oбратные преобразования

Если некоторое преобразование F каждому элементу из области определения сопоставляет свой (отличный от образов других элементов) элемент в множестве значений, т.е. является взаимно однозначным (рис. 8), то можно определить обратное преобразование :

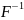Рис.8. Принцип обратного отображения

Если, кроме того, преобразование является линейным (обозначим 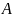), тогда обратное (соответственно 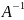) также является линейным. Поскольку композиция «прямого» и обратного преобразований (в любом порядке осуществления) даёт тождественное преобразование:

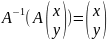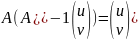и , то матрица обратного преобра-зования равна обратной матрице данного линейного преобразования, т.е.

.

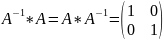Так, в условиях примера 9 легко увидеть, что преобразование C: D→ E является линейным взаимно однозначным преобразованием. Значит, оно обратимо. Обратное преобразование может быть представлено в виде композиции двукратного растяжения плоскости относительно начала координат и симметрии относительно оси Oy. Т.е.

= .
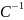
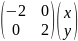