Методические указания

Методические указания разработаны для студентов, обучающихся по направлению 230700.62 Прикладная информатика профиль Прикладная информатика в экономике и направлению 010300.62 Фундаментальная

информатика и информационные технологии очной формы обучения, с целью более глубокого освоения ими курса «Математические методы в компьютерных технологиях», читаемого автором.

Содержание

ВВЕДЕНИЕ

Часть 1. Геометрические свойства линейных и аффинных преобразований

Векторные пространства

Линейные преобразования

Линейные преобразования на R²

Композиция линейных преобразований

Oбратные преобразования

Определитель матрицы линейного преобразования

Аффинные преобразования

Часть 2. Построение переходных изображений

Интерполяция на основе арифметических операций

Арифметические операции над множествами в

Интерполяция изображений методом Минковского

Часть 3. Колориметрия

Введение

Простейшие правила смешения цветов

Аддитивная система представления цветов (RGB)

Субтрактивная система представления цветов (CMY)

Полное описание цветового пространства

Введение

Компьютерные технологии играют всё более важную роль во многих областях человеческой жизни. Поскольку «выдача инструкций» компьютеру происходит, по сути, на языке математики, то для достижения тех или иных целей нужно уметь подобрать удачный математический подход. Важнейший способ математического изучения сложных объектов и явлений – применение к их математическим моделям понятий, используемых для простых математических конструкций. Многие научные построения и алгоритмы связаны с определёнными действиями над объектами; среди них нельзя не выделить сложение и умножение на число (линейные операции), которые могут пониматься очень широко. К примеру, смешение окрашенных световых потоков и увеличение/уменьшение интенсивности светового потока можно интерпретировать как соответственно сложение цветов и умножение на число. В результате понятия, хорошо знакомые по работе с векторами, находят отражение в изучении закономерностей восприятия цвета. Операции сложения и умножения на число и их особенности (применения) в разных ситуациях занимают центральное место в последующих разделах.

Часть 1 геометрические свойства линейных и аффинных преобразований Векторные пространства

Наиболее глубокой конструкцией, связанной с линейными операциями, является линейное пространство.

Определение. Множество L называется линейным пространством, если для ∀ f, g ∊ L и ∀ α , ∊ R определено α ^ f +  ^g, т.е. линейная комбинация любых элементов множества принадлежит этому множеству.

В случае линейного пространства подразумевается, что операции сложения и умножения на число полностью согласованы между собой и позволяют осуществлять содержательные преобразования.

Свойства (аксиомы) операций в линейном пространстве.

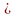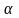Пусть f, g, h L, , R.

1.  f + g = g + f   (коммутативность),  

2.  (f + g) + h = f +(g + h) (ассоциативность),

3. 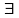элемент 0 L : f + 0 = f ( 0 - нейтральный элемент )

/ можно доказать, что нейтральный может быть только один /,  

4. для 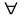f L -f :  f + (-f) = 0  ( -f - противоположный элемент)

/ можно доказать, что для каждого элемента может быть только один противоположный /,  

5. ^ (f + g) = ^ f + ^ g,

6.  ( + ) ^ f = ^ f +  ^ f,

7. ( ^ ) ^ f  ^ ( ^ f),

8. 1 ^ f = f / из этого можно вывести, что - f = (-1) ^ f /.

Примеры 1-2.

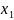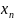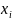1. Обозначим через Rⁿ множество всевозможных упорядоченных наборов из n чисел: Rⁿ = { ( , , … , ) : ∊ R , i = 1, 2, … , n }.

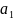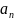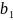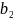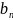Если a =( , , … , ) и b =( , , … , ) – некоторые два из таких наборов и α∊ R , то, определив

i) a + b = ( , , … , ) + ( , , … , ) ( , , …, ),

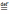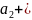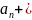ii) α ^ a = α ^ ( , , … , ) (α ^ , α ^ , … , α ^ ) ,

т.е., выполняя линейные действия покоординатно, получим линейное пространство. Соблюдение аксиом сразу следует из того, что они справедливы для каждой координаты отдельно как для операций над действительными числами.

Замечание. Пространство Rⁿ равносильно по своей сути n–мерному векторному пространству, т.е. семейству всех векторов, среди которых есть n штук линейно независимых. Наборы из n чисел соответствуют линейным комбинациям, которые можно составить из базисных векторов, используя коэффициенты наборов.

2. Обозначим через C[a ; b] множество всех непрерывных на отрезке [a ; b] функций.

Если f и g – две такие функции, а α ∊ R то, определив

 i) f + g =  ( f + g)(x) f (x) + g(x) , x∊ [a ; b],

ii) α ^ f = (α ^ f) (x) α ^ f (x) , x∊ [a ; b],

получим линейное пространство. Выполнение аксиом несложно проверить.