§2.4 Потенциальный барьер

Если на зависимости П(x) в силовом поле имеется перепад (см рис.), то на частицу, двигающуюся вдоль оси ОХ действует сила. Говорят о потенциальном барьере. Сила F = - для налетающей слева – направо частицы с кин. энергией ℇ тормозит частицу в классическом понимании и в точке x=x_o она отразится от барьера (точка поворота).

Для случая ступенчатого барьера F .

2.4.1 Ступенчатый барьер конечной высоты

Пусть П(х) =0 в области I и П(х) = П_о в области II.

Случай ℇ П_о

Квантовое решение задачи с использованием ур. Ш. даёт новые, принципиальные результаты:

В области I (x ), имеем, как и для свободной частицы две волны – падающую и отражённую:

Ψ_I = Аe ^jkx + Вe ^{– jkx}

Их суперпозиция – стоячая волна. Плотность вероятности испытывает осцилляции - интерференционный эффект. В классике этого быть не может.

В области II (x

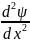+ (ℇ - П_о) ψ =0 (2.5)

Или:

– δ² ψ = 0 , где δ =

Его решение:

Ψ_II = Сe ^{- δx} + De ^δx (2.6)

Реальному физическому смыслу отвечает только условие D = 0.

Используя условия для ψ на границе областей можно получить:

A = , B = 1, C =

Видно, что

1. ψ – функция определяется значением ℇ;

2. можно убедиться, что Ψ_I представляет стоячую волну.

Ψ_I = G cos (kx + φ), где G и φ – постоянные.

Падающая волна отражается от барьера, однако частица с неравной нулю вероятностью может быть обнаружена в области x .

Коэфф. отражения определяют как

R = = │ │² ,

где α₁ = │Ψ_I,пад│² и α₂ = │Ψ_II,отр│²

По мере роста высоты барьера Ψ_II → 0 и частица с меньшей вероятностью проникает в область II.

Случай П_о ℇ

Частица совершает над барьерное движение

Ψ_II = e ^{– jℜ x} Здесь ℜ =

R = ( )² 1

В месте разрыва непрерывности потенциала всегда происходит частичное отражение и частичное проникновение в область за разрывом.

2.4.2.. Прямоугольный барьер. Туннельный эффект

Три области (см. рис.)

Область I (П=0)

Получим: Ψ_I = e ^{– jkx} + Be ^jkx ,

где В определяет амплитуду отражённой волны, k = .

Область II (П_о )

Внутри барьера волна затухает

Ψ_II De ^{– δx} , δ = (2.7)

Повторным отражением в точке а можно в принципе пренебречь.

Область III (П=0)

Здесь существует бегущая волна

Ψ_III De ^{– δa} e ^{– jkx}

Вводят коэфф. пропускания барьера Т:

Т = = e ^{– 2δa} = exp (-2a ), (2.8)

т. к. знаменатель принимается равным 1. Прохождение частицы через барьер носит название туннельного эффекта.

§ 2.5 Частица в потенциальном ящике

(яме с бесконечно высокими стенками)

Три области по оси ОХ. В обл. I и III П_о → , в II потенц. э. П=0.

Стационарное ур. Ш. сходно в обл. II со случаем свободного движения.

В интервале 0 х а

ψ (х) = Аe ^jkx + Вe ^{– jkx}

Условия на границе x =0 дают: А + В =0  А = В, что обеспечит возникновение стоячей волны

ψ (х) = А_о sin kx. Здесь k = .

При x =a обязано быть А_о sin kа= 0, или ak =n π, n= 1, 2, 3…

Подставляя k получают вид функции и избранные значения энергии

Ψ_n (х) = А_о sin x (2.9)

ℇ_n = = – э. дискретна, n – квантовое число.

Амплитуда находится из условия нормировки и одинакова А_о =

Вид функции Ψ_n (х) разных состояний и плотностей вероятности приведен на рис.

Самостоятельно ознакомьтесь с трёхмерной ямой и пологим барьером.

Гл. 3 КВАНТОВЫЙ ГАРМОНИЧЕСКИЙ ОСЦИЛЛЯТОР. МОМЕНТ

ИМПУЛЬСА.