§ 2.1 Квантовое нерелятивистское уравнение движения

1. Временное уравнение

Задача заключается в нахождении уравнения, позволяющего определять не только ψ в момент t_o , но и в последующий момент: ψ(t)

Шредингер предложил ур-е:

j ħ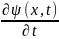 =- + П ψ(x,t) (2.1, а)

для одномерного случая и

j ħ =- + П ψ( ,t) (2.1)

для трёхмерного случая. Оно похоже на волновое при П( ,t) = 0, причём здесь первая производная по времени.

ψ( ,t) – лишь математический способ описания дл нахождения вероятностей и физических величин.

2. Стационарное уравнение

В консервативном поле энергия частицы остаётся неизменной и потенц. энергия зависит только от координат - П( ), что позволяет взять пси функцию в виде волн де Бройля с ℇ = const

ψ(r,t) = ψ( )· (*)

(Сомножитель с одинаковыми ℇ выносится за знак суммы)

Подставляя в (2.1) и сокращая, получают:

- +(ℇ - П) ψ( ,t) = 0 (2.2)

Оно описывает состояния, называемые стационарными.

Отметим для них:

1). Временная часть (*) является гармонической (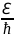 = ω),

2). Вероятность местоположения не зависит от времени (│ψ│² = const )

3). Уравнение (2.2) является ур. для собственных функций энергии.

§ 2.2 Общие свойства решений

2.2.1. Условия, накладываемые на пси-функции

Уравнение дифференциальное (!). Нужно из всех возможных решений выбрать те, которые удовлетворят физическому смыслу.

Общие свойства следующие:

1. ψ( ) – однозначная и непрерывная функция координат.

2. ψ( ) – конечна или где-то равна нулю. │ψ│²

3. Сама ψ( ) и её производные должны быть непрерывны. Это даже вытекает из самого ур-я.

Условия называются стандартными.

Методика решения (2.2) исходит из вида П( ): желательно использование простых зависимостей, что достигается разделением интервала значений на характерные участки интегрирования (оно неизбежно). Подбор постоянных интегрирования также важный момент.

Значения функций и их производных на границах этих участков обязаны совпадать (сшиваться):

Например: ψ_I(l)│_l-0 = ψ_II(l)│_l+0

( )_I│_l-0 =( )_II│_l+0

Наконец, оставляем те ψ, которые ведут себя на выделенном участке хорошо при r .

Используем условие нормировки, чтобы получать разумные │ψ│² .

d ³r = 1

Тем самым определяется амплитудный коэффициент при ψ .

§ 2.3 Свободное движение частиц

Плоская волна де Бройля вдоль оси ОХ:

ψ_p(x) = A ⁾

Здесь ℇ ничем не ограничено (любое положительное), │ψ_р│² = const

т.к. все точки эквивалентны. Уравнение Шр. для такого движения при

П(х) =0 приобретает вид:

+ ℇ ψ = 0 (2.3)

Или

+ k² ψ =0 (2.3, a)

Его общее решение

ψ = Аe ^jkx + Вe ^{– jkx} (2.4)

Здесь k² = ℇ  ℇ = =

Иначе, стационарное решение

ψ = Аe ^{jpx/ ℏ} + Вe ^{- jpx/ ℏ} (2.4, a)

Если принять, что частица движется слева направо и положить В = 0, то выходим на совпадение с выражением для волны де Бройля. Спектр значений для ℇ является непрерывным пока движение не ограничено замкнутостью объёма. Доступное значение ℇ всегда больше П_min. Состояния с ℇ 0 соответствуют локализации частицы.