Задача 2.6.

Определить манометрическое давление в трубопроводе А, если высота столба ртути по пьезометру h₂ =25 см. Центр трубопровода расположен на h₁ =40 см ниже линии раздела между водой и ртутью.

Методические указания к решению задачи

Находим давление в точке В. Точка В расположена выше точки А на величину h₁, следовательно, давление в точке В будет равно

.

В точке С давление будет такое же, как в точке В, то есть

.

Определим давление в точке C, подходя, справа

.

Приравнивая оба уравнения, получаем

.

Из уравнения находим манометрическое давление

.

Задача 2.7.

Определить все виды гидростатического давления в баке с нефтью на глубине H = 3 м, если давление на свободной поверхности нефти 200 КПа. Плотность нефти ρ = 0,9 т/м³.

Методические указания к решению задачи

1. Абсолютное гидростатическое давление у дна

2. Избыточное (манометрическое) давление у дна

3. Избыточное давление создаваемое столбом жидкости

4. Избыточное давление на свободной поверхности

Задача 2.8.

Стальная труба с внутренним диаметром d = 600 мм работает под давлением р = 3 МПа. Найти необходимую толщину стенок трубы, если допустимое напряжение для стали составляет [] = 150 МПа.

Методические указания к решению задачи

Из условия прочности находим толщину стенок трубы:

 = [],

 = [],

Задача 2.9.

Определить давление рo воздуха в напорном баке по показанию ртутного манометра. Какой высоты Н должен быть пьезометр для измерения того же давления рo? Высоты h=2,6 м; h₁=1,8 м; h2=0,6 м. Плотность ртути ρ= 13600 кг/м3, воды ρ= 1000 кг /м3.

Методические указания к решению задачи

Задача 2.10.

Определить силу F, действующую на шток гибкой диафрагмы, если ее диаметр D = 200 мм, показания вакуумметра р_вак = 0,05 МПа, высота h = 1 м. площадью штока пренебречь. Найти абсолютное давление в левой полости, если h_атм = 740 мм. рт. ст.

Методические указания к решению задачи

Задача 2.11.

На поршень одного из сообщающихся сосудов, наполненных водой, действует сила Р₁ = 200 Н, а на поршень второго сосуда Р₂ = 300 Н. определить разность уровней жидкости в сосудах h, если диаметр первого поршня d₁ = 0,1 м, второго поршня d₂ = 0,15 м.

Методические указания к решению задачи

Задача 2.12.

Цилиндрический сосуд заполнен водой на высоту h = 0,6 м. Диаметр сосуда D = 40 cм, диаметр горловины d = 10 см. На свободную поверхность жидкости при помощи поршня приложена сила Р = 50 Н. Определить силу давления р₁ на дно сосуда, абсолютное давление в точке, лежащей на половине высоты сосуда.

Методические указания к решению задачи

Силу давления р₁ на дно сосуда можно определить по следующей формуле:

р₁ = (р_о +γ·h_c) ·w,

где р_о = 4Р / πd²; h_{c =} h; ω = π D ² / 4.

Тогда абсолютное давление в точке на половине высоты

р = р_о +γ· .

Задача 2.13.

При гидравлическом испытании трубопровода диаметром d = 200 мм и длиной 250 м давление в трубе было повышено до 3 МПа. Через час давление снизилось до 2 МПа. Сколько воды вытекло через неплотности?

Методические указания к решению задачи

Объем воды в трубопроводе можно определить: w=

Изменение давления за время испытания:

Δp = p₁ – p₂.

Принимая коэффициент объемного сжатия воды находим количество воды, вытекающей через неплотности, по формуле

 ω = –_v· w·р.

Задача 2.14.

Определить усилие, которое развивает гидравлический пресс, имеющий d₂ = 250 мм, d₁ = 25 мм, а = 1 м и b = 0,1 м, если усилие, приложенное к рукоятке рычага рабочим, N = 200Н, а КПД равен 0,8.

Методические указания к решению задачи

Усилие в гидравлическом прессе можно определить по формуле:

Задача 2.15.

При гидравлическом испытании системы объединенного внутреннего противопожарного водоснабжения допускается падение давления в течение 10 мин. на p = 4,97104 Па. Определить допустимую утечку W при испытании системы вместимостью W = 80 м³. Коэффициент объемного сжатия _w= 5 10^-10 Па^-1.

Методические указания к решению задачи

Допустимую утечку W определяем из формулы

;

;

Задача 2.16.

В боковую стенку сосуда А, наполненного водой, вставлена пьезометрическая трубка В. Определить абсолютное давление р на свободной поверхности жидкости в сосуде, если под действием этого давления вода в трубке поднялась на высоту h = 1,5 м.

Методические указания к решению задачи

Давление на свободной поверхности жидкости в сосуде равняется давлению в сечении а пьезометра и определяется по основному уравнению гидростатики:

р = р_о + γh.

Отсюда, зная давление на свободной поверхности р_о = р_атм и удельный вес воды γ находим р.

Задача 2.17.

Сосуд заполнен водой, занимающей объем W₁= 2 м³. На сколько уменьшится и чему будет равен этот объем при увеличении давления на величину 200 бар при температуре 20^oС ? Модуль объемной упругости для воды при данной температуре Е_о = 2110 МПа.

Методические указания к решению задачи

Изменение объема жидкости можно определить из уравнения:

ΔW = – β_wW Δp.

Затем определяем коэффициент объемного сжатия из уравнения:

β_w = 1 / Е_o

Увеличение давления Δр = 200 бар = 20·10⁶ Па.

Находим ΔW.

Тогда искомый объем будет равен:

W₂ = W₁ – ΔW.

Задача 2.18.

В цилиндре под поршнем находится воздух при манометрическом давлении 0,02 МПа. Определить перемещение поршня и давление в конце процесса изотермического сжатия, если на поршень дополнительно действует груз массой 5 кг. Диаметр поршня d = 100 мм. Высота начального положения поршня h = 500 мм.

Методические указания к решению задачи

Дополнительную силу, создаваемую грузом, можно найти следующим образом:

F= mg .

Тогда дополнительное давление от груза:

Конечное давление:

p₂ = p₁ + Δp = p_атм + р_ман + Δр.

Объем воздуха в цилиндре до начала действия груза:

.

Объем воздуха после изотермического сжатия:

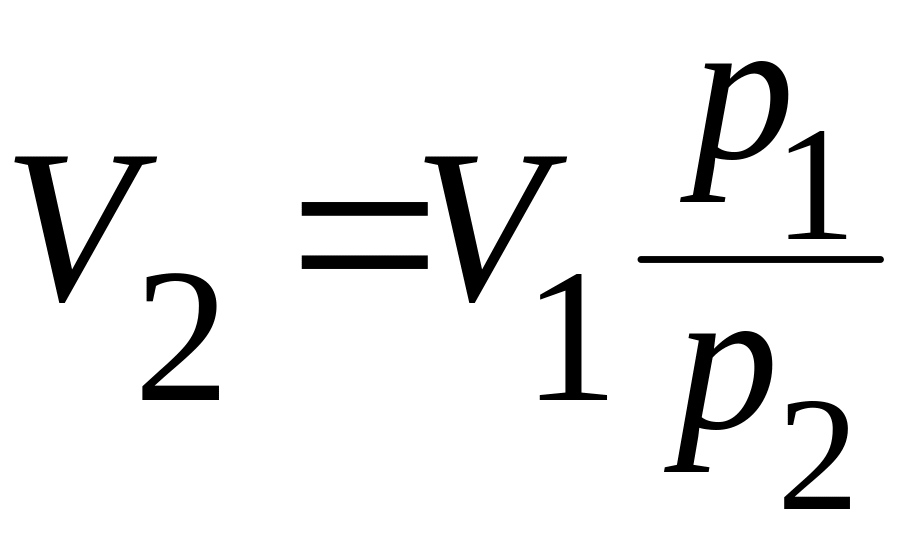
Тогда, высота положения поршня после сжатия

Перемещение поршня в цилиндре в результате сжатия

Δh = h₁ – h₂.

Задача 2.19.

Имеется труба с переменным поперечным сечением и напорным движением жидкости. Определить среднюю скорость в первом сечении , если известно, что диаметр первого сечения , диаметр второго сечения и средняя скорость во втором сечении .

Методические указания к решению задачи

Находим площади живых сечений:

^{; .}

Подставляя эти значения в уравнение неразрывности

^,

получим

^,

т. е. для случая круглой трубы, сплошь заполненной жидкостью, средние скорости обратно пропорциональны квадратам диаметров соответствующих внутренних сечений трубы.

Скорость в первом сечении будет равна, м/с

^,

Задача 2.20.

Определить абсолютное давление в сосуде по показанию жидкостного манометра, если известно: h₁= 2м; h₂ = 0,5 м; h₃ = 0,2 м; ρ_м = 880 кг/м³.

Методические указания к решению задачи

Давление в точках А и В равно, так как они лежат в одной горизонтальной плоскости, проходящей в однородной жидкости, поэтому

р_ат + ρ_мgh₃ +ρ_ртgh₂ = р_абс + ρ_вgh₁,

где ρ_рт - плотность ртути, ρ_рт = 13600 кг/м³;

ρ_в – плотность воды, ρ_в = 1000 кг/м³.

Тогда абсолютное давление в сосуде можно определить

р_абс = р_ат + ρ_мgh₃ +ρ_ртgh₂ - ρ_вgh₁