26) Көпмүшенің жіктелу өрісі.

а) Келтірілмейтін көпмүше

Келтірілмейтін көпмүше - едәуір төменгі дәрежелі көбейткіштерге жіктелмейтін көпмүше. Көпмүшенің көбейткіштерге жіктелу мүмкіңдігі осы көпмүшенің кандай сан аймағында (облысында) карастырылатындығына тәуелді. Мысалы, x ³ + 2 көпмүшесі, егер коэффициентгеріретінде тек рационал сандар ғана алынған болса, онда ол келтірілмейтін екі көбейткішке жіктелмейді. Егер коэффициенттері ретінде кез келген нақты сандар алынатын болса:

x+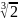 және x²-x³ + көбейткіштеріне жіктеледі, ал егер коэффициентгері комплекс саңдар болса, мынадай үш көбейткішке жіктеледі:

x+ , x- * , x- *

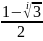
Жалпы жағдайда көпмүшелерге катысты келтірілмейтіндік кез келген өріс үшін анықгалады.

б) P-өріс, f(x) P[x]

Келтірілмейтін көпмүше

f(x)=a₀+a₁x+a₂+x²+…a_nx⁴

h(x), q(x)€P[x].

I=P[x] идеал: r(x)*ICI кез келген r(x) € k.

Егер h(x)-q(x)=(-x)*s(x)

Онда h(x)=q(x).

Эквавалентті

1 h(x)=h(x).

2 h(x)=q(x)=> q(x)=h(x)

3 h(x)=q(x); q(x)=k(x)=>h(x)=k(x)

h(x)-k(x) = h(x)-q(x)+q(x)-k(x) Экваваленттік қатынас

P[x]-/г = P[x]/f(x)={r(x)+f(x))|r(x) € P[x]}

(f(x))={q(x)*f(x)/q(x) € P[x]} идеал P[x].

Теорема. Егер f(x) P[x] сақина онда келтірілмейтін көпмүше болса,онда P[x]/f(x) фактор жиыны өріс болуы . Осы өрісте f(x) көпмүшесі түбірге ие.

P[x]/f(x)={A,B,C… }

A={a(x) € P[x]| кез келген q(x) € P[x].

q(x)~a(x)}

A+B={a(x)+b(x)|

a(x) € A,b(x) € B

A*B={a(x)*b(x) a(x) € A

b(x) € B}

27 Қарапайым ақырлы өрістер

a) Бүтін сандар сақинасы

b) Идеалдар

c) Максимальді идеал бойынша фактор сақина

А) Коне́чное по́ле, или по́ле Галуа́ в общей алгебре — поле, состоящее из конечного числа элементов. Число элементов в поле называется его поря́дком.

Конечное поле обычно обозначается или (сокращение от Galois field) и называется полем Галуа порядка [1], где — число элементов поля. С точностью до изоморфизма конечное поле полностью определяется его порядком, который всегда является степенью какого-нибудь простого числа, то есть , где — простое число, а — любое натуральное число. При этом будет являться характеристикой этого поля[2].

Понятие конечного поля используется в теории чисел[3], теории групп[3], алгебраической геометрии[3], криптографии[4].

Конечным полем называется конечное множество, на котором определены произвольные операции, называемые сложением, умножением, вычитанием и делением, (кроме деления на 0) в соответствии с аксиомами поля[5].

Мультипликативная группа конечного поля — циклична. То есть все ненулевые элементы поля образуют группу относительно операции умножения (эта группа называется мультипликативной группой поля и обозначается ). Эта группа является циклической, то есть в ней есть порождающий элемент, а все остальные элементы получаются возведением в степень порождающего[5]. То есть, существует — порождающий элемент, такой что для любого , можно записать:

.

Порождающий элемент называется также примитивным элементом поля Поле содержит примитивных элементов, где — функция Эйлера.[6]

Также поле обладает рядом других свойств:

Согласно малой теореме Ферма, каждый элемент поля удовлетворяет равенству [2].

Поле содержит в себе в качестве подполя тогда и только тогда, когда является делителем [1].

Если — неприводимый многочлен степени , то поле содержит любой его корень , причём множество всех его корней имеет вид . Таким образом, является полем разложения многочлена над полем [7].

Для каждого конечного поля и натурального числа произведение всех нормированных неприводимых над многочленов, степень которых делит , равно В частности, сумма степеней таких многочленов равна [8].

Число нормированных многочленов степени n, неприводимых над полем определяется по формуле , где — функция

Поле с простым числом элементов и связь с кольцами вычетов[править | править вики-текст]

Наиболее известный пример конечного поля — поле классов вычетов по модулю простого числа , обозначаемое [10]. Это поле можно представить следующим образом. Для простого числа элементами поля будут числа . Сложение и умножение определены как сложение и умножение чисел с приведением результата по модулю [11]. Ниже приведены примеры таких полей с двумя элементами и тремя элементами.

Любое поле простого порядка может быть представлено кольцом вычетов (т.е. любое поле из элементов изоморфно полю ). Однако не каждое конечное поле является кольцом вычетов, и не каждое кольцо вычетов по модулю натурального числа является полем. Кольцо является полем тогда и только тогда, когда — простое число[12]. Если же — составное число, то не все ненулевые элементы кольца обратимы. Например, — не поле, так как элемент в этом кольце не обратим. Тем не менее, существует поле, состоящее из четырёх элементов (см. ниже).

Характеризация конечных полей[править | править вики-текст]

Характеристика каждого конечного поля является простым числом. Пусть — конечное поле. Тогда оно состоит из элементов, где — характеристика поля , а натуральное число — степень поля над его простым подполем[2].

Согласно теореме о существовании и единственности конечных полей, для каждого простого числа и натурального числа существует конечное поле из элементов и любое конечное поле из элементов изоморфно полю разложения многочлена над полем . Данная теорема позволяет говорить о вполне определённом поле данного порядка (то есть о поле Галуа из элементов)[13].

Построение[править | править вики-текст]

Поле при n > 1 можно построить как факторкольцо , где — неприводимый многочлен степени n над полем . Таким образом, для построения поля из элементов достаточно отыскать многочлен степени , неприводимый над полем (такой многочлен всегда существует). Элементами поля являются классы вычетов многочленов степени меньшей с коэффициентами из по модулю главного идеала, порождённого многочленом .

Элемент является корнем многочлена и поле порождается этим элементом над полем , поэтому переход от поля к полю называется присоединением к полю корня неприводимого многочлена .[14][15]

b) идеалы

Идеал — одно из основных понятий общей алгебры. Наибольшее значение идеалы имеют в теории колец, но также определяются и для полугрупп, алгебр и некоторых других алгебраических структур. Название «идеал» ведёт своё происхождение от «идеальных чисел». Простейшим примером идеала может служить подкольцо чётных чисел в кольце целых чисел. Идеалы дают удобный язык для обобщения результатов теории чисел на общие кольца.

Например, в кольцах вместо простых чисел изучаются простые идеалы, как обобщение взаимно простых чисел вводятся взаимно простые идеалы, можно доказать аналог китайской теоремы об остатках для идеалов.

В некотором важном классе колец (т. н. дедекиндовых) можно даже получить аналог основной теоремы арифметики: в этих кольцах каждый ненулевой идеал можно единственным образом представить как произведение простых идеалов.

Определение[править | править вики-текст]

Для кольца идеалом называется подкольцо, замкнутое относительно умножения на элементы из . При этом идеал называется левым (соответственно правым), если он замкнут относительно умножения слева (соответственно справа) на элементы из . Идеал, являющийся одновременно левым и правым, называется двусторонним. Двусторонний идеал часто называется просто идеалом. В коммутативном случае все эти три понятия совпадают и всегда применяется термин идеал.

Более точно: Идеалом кольца называется такое подкольцо кольца , что

1. произведение (условие на правые идеалы);

2. произведение (условие на левые идеалы).

Аналогично для полугруппы её идеалом называется подполугруппа, для которой верно какое-нибудь из этих условий (или оба для двустороннего идеала), то же самое и для алгебры.

Замечание[править | править вики-текст]

Для -алгебры (алгебры над кольцом ) идеал кольца может, вообще говоря, не быть идеалом алгебры , так как это подкольцо необязательно будет подалгеброй, то есть ещё и подмодулем над . Например, если есть -алгебра с нулевым умножением, то множество всех идеалов кольца совпадает с множеством всех подгрупп аддитивной группы , а множество всех идеалов алгебры совпадает с множеством всех подпространств векторного -пространства . Однако в случае, когда — алгебра с единицей, оба эти понятия совпадают.

Связанные определения[править | править вики-текст]

• Для любого кольца само и нулевой идеал являются идеалами (двусторонними). Такие идеалы называются тривиальными. Собственные идеалы — это идеалы, образующие собственное подмножество, то есть не совпадающие со всем [1][2]

• Многие классы колец и алгебр определяются условиями на их идеал или решётку идеалов. Например:

• Кольцо, не имеющее нетривиальных двусторонних идеалов, называется простым.

• Кольцо, не имеющее нетривиальных идеалов (не обязательно двусторонних), является телом. См. также: кольцо главных идеалов, артиново кольцо, нётерово кольцо.

• С любым коммутативным кольцом с единицей связано топологическое пространство — спектр кольца, точками которого являются все простые идеалы кольца , отличные от , а замкнутые множества определяются как множества простых идеалов, содержащих какое-то множество элементов кольца (или, что то же, идеал , порождённый этим множеством). Эта топология называется топологией Зарисского.

• Понятие идеала тесно связано с понятием модуля. Идеал (правый или левый) можно определять как подмодуль кольца, рассмотренного как правый или левый модуль над собой.

Свойства[править | править вики-текст]

• Левые идеалы в R являются правыми идеалами в т. н. противоположном кольце — кольце с теми же элементами и тем же сложением, что и данное, но с умножением определенным , и наоборот.

• Двусторонние идеалы в кольцах и алгебрах играют ту же роль, что и нормальные подгруппы в группах:

• Для всякого гомоморфизма ядром является идеал, и обратно, всякий идеал — ядро некоторого гомоморфизма.

• Более того, идеал однозначно (с точностью до изоморфизма) определяет образ гомоморфизма, ядром которого он является: изоморфен факторкольцу (факторалгебре) .

• В кольце целых чисел все идеалы главные и имеют вид , где .

• Пересечение идеалов также является идеалом (часто, особенно в коммутативной алгебре, пересечение называется наименьшим общим кратным).

Типы идеалов[править | править вики-текст]

• Главный идеал: Идеал, порожденный одним элементом.

• Конечнопорождённый идеал

• Минимальный идеал

• Максимальный идеал: Собственный идеал I называется максимальным, если не существует собственный идеал J такой, что I — собственное подмножество J. Факторкольцо по максимальному идеалу является полем.

• Модулярный идеал

• Нильпотентный идеал

• Первичный идеал

• Примарный идеал

• Простой идеал

• Радикальный идеал: Идеал, совпадающий со своим радикалом.

Основные конструкции[править | править вики-текст]

• Главные идеалы. Если p принадлежит R, a k любое целое число то — будет минимальным правым идеалом, содержащим p, а — минимальным левым идеалом в R. Они называются, соответственно, главными правым и левым идеалом, порожденными p. В коммутативном случае эти идеалы совпадают и обозначаются также (p). Если кольцо R содержит единичный элемент, то так как , главные идеалы, порождённые a можно записать и соответственно. Всякий идеал, содержащий элемент p, содержит и главный идеал, им порождённый.

• Идеал, порождённый множеством элементов. Пересечение произвольного семейства левых идеалов кольца R — левый идеал кольца R. Поэтому для всякого подмножества M кольца R существует минимальный левый идеал, его содержащий, а именно — пересечение всех левых идеалов, содержащих множество M. (То же верно для правых и двусторонних идеалов.) Для кольца R с единичным элементом минимальный левый идеал представляет собой множество конечных сумм вида , минимальный правый идеал — множество конечных сумм вида , минимальный двусторонний идеал — множество конечных сумм вида , где mi — произвольные элементы множества M, а ri,r'i — произвольные элементы кольца R. Если кольцо не содержит единицы то минимальный левый идеал будет иметь вид , минимальный правый , минимальный двусторонний , где все — любые целые числа. Эти идеалы называются порождёнными множеством M. В коммутативном случае все они совпадают и обозначаются так: (M). Идеалы, порождённые конечным множеством, называются конечнопорождёнными.

• Сумма идеалов. Если в кольце R задано произвольное семейство идеалов , их суммой называется минимальный идеал, который их всех содержит. Он порождён объединением этих идеалов, и его элементами являются любые конечные суммы элементов из их объединения. (Само объединение идеалов обычно идеалом не является.) Относительно суммы все (левые, правые или двусторонние) идеалы кольца (или алгебры) образуют решётку. Каждый идеал является суммой главных идеалов. Часто, особенно в коммутативной алгебре, сумма называется наибольшим общим делителем).

• Пересечение идеалов (как пересечение множеств) всегда является идеалом. С другой стороны, объединение двух идеалов является идеалом только тогда, когда один из них — подмножество другого. Действительно, пусть и — два (левых) идеала, ни один из которых не является подмножеством другого, и является левым идеалом. В этом случае, очевидно, — наименьший идеал, содержащий и , то есть . Существует элемент . Тогда для любого , так как в этом случае , следовательно, и , поэтому — противоречие.

• Произведение идеалов. Произведением идеалов I и J называется идеал IJ, порождённый всеми произведениями ab, где a — элемент идеала I, b — элемент идеала J. Бесконечное произведение идеалов неопределено.

• Частное идеалов. В коммутативном кольце для идеала I, отличного от нуля, и идеала J определёно их частное — идеал . Этот идеал называется аннулятором идеала I в случае, когда J=(0), .

• Радикал идеала I — это множество . Оно тоже является идеалом кольца A, если только кольцо A коммутативно. В случае, когда I=(0), этот идеал называется нильрадикалом кольца A. Его элементами являются все нильпотентные элементы кольца. Если коммутативное кольцо не имеет нильпотентных элементов, кроме нуля, (имеет нулевой нильрадикал), — оно называется радикальным. Идеал I называется радикальным, если он совпадает со своим радикалом. В этом случае факторкольцо R/I не имеет нильпотентных элементов, кроме нуля.

• Индуктивный предел. Если задано семейство (цепочка) идеалов , занумерованное линейно упорядоченным множеством A, так что для любых индексов из A идеал содержится в идеале , тогда их объединение является идеалом — индуктивным пределом данной цепочки идеалов. Этот идеал также совпадает с суммой всех идеалов из цепочки. Тот факт, что индуктивный предел всегда существует, означает, что множество всех идеалов кольца R индуктивно упорядочено, и к нему применима лемма Цорна. Она часто используется для построения максимальных идеалов с какими-то дополнительными свойствами (см. максимальный идеал, простой идеал, кольцо главных идеалов).

• Образ идеала при гомоморфизме. Обычно образ идеала при гомоморфизме НЕ является идеалом, однако если гомоморфизм сюръективен, то тогда является. В частности, так как гомоморфизм факторизации всегда сюръективен, при факторизации каждый идеал переходит в идеал.

• Прообраз идеала при гомоморфизме. Если — гомоморфизм колец, его ядро является двусторонним идеалом. Более общо, если I — произвольный идеал в кольце B, его полный прообраз является идеалом (левым, правым или двусторонним, в зависимости от того, каков идеал I).

• Гомоморфизм факторизации по идеалу. Если I — двусторонний идеал в кольце R, по нему можно определить отношение эквивалентности на R по правилу: x ~ y тогда и только тогда, когда разность x-y принадлежит I. Проверяется, что если в сумме или произведении один из операндов заменить на эквивалентный, новый результат будет эквивалентен исходному. Таким образом операции сложения и умножения становятся определенными на множестве R/I классов эквивалентности, превращая его в кольцо (коммутативность и наличие единицы переносятся с кольца R, если они есть). Одновременно с этим кольцом определён гомоморфизм факторизации (канонический гомоморфизм) , который каждому элементу a из R ставит в соответствие класс эквивалентности, в котором он содержится. Класс эквивалентности элемента a есть множество элементов вида a+i по всем i из идеала I, поэтому он обозначается a + I, но иногда используется и общее обозначение для класса эквивалентности [a]. Поэтому . Кольцо R/I при этом называется факторкольцом кольца R по идеалу I.

С) Максимальным идеалом коммутативного кольца называется всякий собственный идеал кольца, не содержащийся ни в каком другом собственном идеале.

Свойства[править | править вики-текст]

• Множество всех идеалов кольца индуктивно упорядочено по отношению включения, поэтому (Лемма Цорна) во всяком кольце максимальные идеалы существуют, более того, для всякого собственного идеала I кольца R существует максимальный идеал кольца R, который его содержит.

• (Считаем далее, речь идёт о кольцах с единицей.)

Если элемент a кольца R не обратим, тогда все элементы кольца, кратные ему, образуют собственный идеал. Поэтому каждый необратимый элемент кольца содержится в некотором максимальном идеале. Если элемент a обратим, всякий идеал, который его содержит, совпадает со всем кольцом, поэтому обратимые элементы не содержатся ни в каком собственном идеале, соответственно и ни в каком максимальном.

• Если все необратимые элементы кольца R образуют идеал, он является максимальным, и притом единственным - других максимальных идеалов в кольце R нет. (Верно и обратное: если в кольце R максимальный идеал единствен, он включает в себя все необратимые элементы кольца.) В этом случае кольцо R называется локальным кольцом.

• Характеристическое свойство максимального идеала: идеал кольца максимален, тогда и только тогда, когда факторкольцо является полем (в нём каждый элемент обратим).

• Если кольцо R имеет структуру банаховой алгебры над полем комплексных чисел С, факторкольцо по максимальному идеалу R/I изоморфно C. В этом случае идеал I определяет гомоморфизм кольца R в поле C, ядром которого является идеал I.

Для каждого a существует единственное число , такое что (e - единица алгебры R). Соответствие и есть тот самый гомоморфизм.

• Из характеристического свойства следует, что всякий максимальный идеал является простым.

Примеры[править | править вики-текст]

• В кольце целых чисел Z максимальными идеалами являются все простые идеалы: если p - простое число, тогда идеал (p)=pZ максимален. Например, чётные числа образуют максимальный идеал, а числа, кратные 4 - образуют идеал, но не максимальный - этот идеал содержится в идеале чётных чисел.

• В кольце многочленов k[X,Y], где k - алгебраически замкнутое поле, максимальные идеалы имеют вид .

• Кольцо степенных рядов над полем k - локальное кольцо. Необратимые элементы - те, которые не содержат свободного члена. Они образуют идеал. Он - единственный максимальный идеал в этом кольце.