30. Алгебралық сандар өрісі
21
Нақты көпмүшелердің нақты түбірлері
Штурм жүйесі –көпмүшелер үшін нақты түбірлер санын анықтау жане олардың түбірлерін жекелеу тәсілдерінің бірі.
Мысалы
көпмүшесін қарастырсақ.
f€ R[X] жане f-тің еселі түбірлері жоқ болсын.|R өрісіндеі f0,f1,…fk көпмүшелер тізбегі үшін:
1.f0=f, ал fk көпмүшесінің нақты түбірлері жоқ.
2.көрші көпмүшелердің ортақ түбірлері жоқ.
3.егер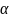
нақты саны
(0<i<k)
аралық копмүшесінің түбірі болса,онда
сандарының таңбалары қарама-қарсы.
4.
егер
нақты саны f-тің түбірі болса,онда f0*f1
функциясы
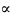нүктесі арқылы откенде танбасын минустан
плюске өзгертеді.
Осы 4 шарт орындалса,онда f0,f1,…fk тізбегі f көпмүшесінің Штурм жүйесі деп аталады.
а<
б кез келген нақты сандар f€
R[X] еселі түбірлері жоқ көпмүше,ал
f0,f1,…fk көпмүшелері f-тің Штурм
жүйесі болсын.Онда
W(a)
W(b) және (a,b) интервалында f-тің нақты
түбірлер саны W(a)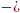
W(b) айырымына тең болады.
Дәлелдеу. Қандай да бір нүктесінде нолге айналмайтын кез-келген үзіліссіз функция нүктесінің маңайында да таңбасын өзгертпейді,ал әр көпмүше үзіліссіз функция болады және оның секірмелері f0,f1,…fk-1 көпмүшелерінің түбірлерінде ғана болуы мүмкін.
22. Көпмүшелер сақинасы
N натурал сандар, Q рационал сандар, R нақты сандар, С комплекс сандар, Z бүтін сандар жиындары, К символын осы саедардың белгіленуі ретінде қолданылады, яғни К арқылы
Z,Q,C,Z,Rn
(n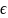
N)
жиындарының кез келген біреуін
белгілейміз. Бұл жағдайда K жиынына
сақина атауын пайдаланамыз.
Q,R,C,Zp (p-жай сан) жағдайында өріс деп атап, Р санын олардың жалпы белгіленуі ретінде қолданамыз.
A)Кез келген көпмүшені стандарт түрде жазуға болады. Ол үшін: Көпмүшенің әрбір мүшесін стандарт түрде жазу керек; Ұқсас мүшелерді біріктіру керек.
Көпмүшені бірмүшеге көбейту үшін бірмүшені көпмүшенің әрбір мүшесіне көбейтіп, шыққан көбейтінділерді қосады
Көпмүшелердің алгебралық қосындысын стандарт түрдегі көпмүше ретінде жазу үшін жақшаларды ашып, ұқсас мүшелерді біріктіру керек.
Көпмүшені көпмүшеге көбейту үшін бірінші көпмүшенің әрбір мүшесін екінші көпмүшенің әрбір мүшесіне көбейтіп, шыққан көбейтінділерді қосу қажет.
Көпмүшені бірмүшеге бөлу үшін көпмүшенің әрбір мүшесін бірмүшеге бөліп, шыққан бөлінділерді қосу керек
Б,В) Бір айнымалылы көпмүшелік, полином деп математикада келесі функцияны айтады
{\displaystyle
F(x)=c_{0}+c_{1}x+\cdots +c_{n}x^{n},}
мұндағы {\displaystyle
c_{i}}
тұрақты коэффициенттер,
ал {\displaystyle
x}x —
айнымалы.
Көпмүшеліктер элементар
функциялардың маңызды
табы
болып
табылады.
n айнымалылы көпмүшелік (немесе полином) деп келесі түрдегі шекті қосындыны айтады
{\displaystyle
\sum _{I}c_{I}x_{1}^{i_{1}}x_{2}^{i_{2}}\cdots x_{n}^{i_{n}}}
,
мұндағы 
{\displaystyle
I=(i_{1},i_{2},\dots ,i_{n})} теріс
емес бүтін
сандар жиыны
(мультииндекс деп
аталатын), 
{\displaystyle c_{I}} —
тек
мультииндекс I-ға
тәуелді
(«көпмүшелік
коэффициенті
деп
аталатын»)
сан.
Жекеше түрі, бір айнымалылы көпмүшелік келесі шекті қосынды болып табылады
{\displaystyle
c_{0}+c_{1}x^{1}+\dots +c_{n}x^{n}.}
Көпмүшелік
коэффициенттері әдетте белгілі
бір коммутативті {\displaystyle
R}
R
сақинасынан (көбінесе өрістен,
мысалы, нақты
сандар немесе комплекс
сандар өрісінен)
алынады. Бұл жағдайда қосу мен көбейту
операцияларына қатысты көпмүшеліктер
{\displaystyle
R[x_{1},x_{2},\dots ,x_{n}].}
деп белгіленетін сақина (оның үстіне {\displaystyle R}R сақинасында нөл бөлгіштерінсіз ассоциативті-коммутативті сақинадағы алгебраны) құрайды.
Егер үлкен коэффициенті бірге тең болса көпмүшелік унитарлы немесе келтірілген деп аталады
түріндегі
көпмүшеліктерді бірмүшелік немесе моном деп
атайды
мультииндексіне
сәйкес келетін бірмүшелікті бос
мүше деп
атайды.
Көпмүшелік екі нөл емес мүшесі болса оны екімүшелік немесе бином дейді,
Көпмүшелік үш нөл емес мүшесі болса оны үшмүшелік деп атайды.
(нөл
емес) бірмүшеліктің толық
дәрежесі деп
мына бүтін санды айтады
Көпмүшелік дәрежесі деп оның бірмүшеліктерінің ең максималды дәрежесін айтады, нөлдің дәрежесі болмайды
Коэффициенттері {\displaystyle
c_{I}}
нөл
болмайтындай мультииндекстер
жиынын көпмүшелік
игерушісі,
ал оның дөңес
қабығын - Ньютон
көпжағы дейді.
3.Айталық K[x]-K сақина үстінде жасалған көпмүшелер өрісі болсын.
Теорема: К біртұтас аймақ болса, K[x] тан алынған кез – келген n дәрежелі көпмүшенің түрлі түбірлері саны n аспайды.
Нәтиже.Егер көпмүше n-нен артық сандағы түрлі түбірлерге ие болса, онда f – нолдік емес көпмүше болады.
Көпмүшеліктедің алгебралық және функционалдық теңдіктері анықталады.
Теорема: Айталық K[x]-K ақырсыз біртұтастық аймақ үстінде жасалған көпмүшелер сақинасы болып, K[x] тең алған f және g функциялар тең болуы үшін олар анықталған f және g* функциялары тең болуы қажетті және жеткілікті.
Қалдықпен бөлу туралы теорема.
Айталық f[x]– F- өріс үстінде жасалған көпмүшелер сақинасы, және f(x) оның негізгі жиыны болсын.
Теорема: Егер көпмүше ноль емес болса, онда кез – келген көпмүше үшін F(х) те
F = hg + z, degz<degh, немесе z = 0 шарттарды орындайтын g және z көпмүше табылады.
1-Салдар: Егер F өріс болса, онда көрмүшелер өрісі болған F[x] евклидті сақина болады.
2-Cалдар: F өрісі үстінде жасалған көпмүшелер сақинасы F[x] бас идеалдар сақинасы болады.
3-Салдар. Егер F өріс болса, онда көпмүшелер сақинасы F[x] факториалды болады.