1.1.4 Расчет линий напряжённости е поля

Уравнение любой линии Е поля является уравнением дуги окружности, пересекающейся с электрическими осями с координатами центра:

; ,

где β – угол между линиями соединяющими точку пересечения κ-той линии напряженности Е с плоскостью нулевого потенциала с электрическими центрами цилиндров.

Линии Е поля должны быть построены так, чтобы весь поток Е был поделён ими на равное целое число трубок. Для этого, при переходе от любой линии Е к соседней необходимо изменить угол β на постоянную величину .

Вычисление :

За начальную линию Е принимают линию, соединяющую электрические оси. Угол для неё равен: .

Вторую линию строят (от руки) таким образом, чтобы в результате пересечения обеих линий с эквипотенциальной линией получался квадрат.

Соединяя любую точку отрезка второй линии, являющегося верхней стороной квадрата, с электрическими осями находят угол β₂ и вычисляют :

Поскольку диапазон изменения , то число линий Е поля:

Полученный результат округляется до ближайшего целого чётного .

После этого уточняется :

; ; .

Округляем до ближайшего чётного числа ;

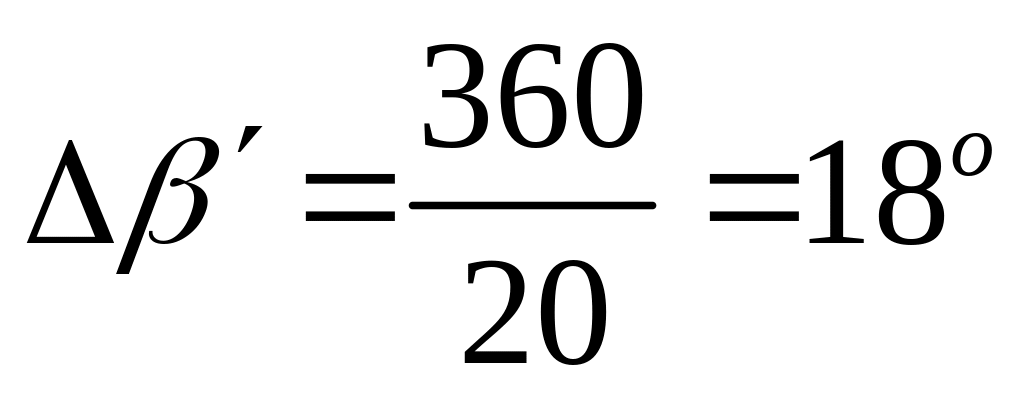
Расчет координат сведен в таблицу 1.2.

Таблица 1.2 Расчет линий напряженности поля

κ		, (м)	, (м)
1	0	∞	∞
2	18	0,209	0,22
3	36	0,094	0,116
4	54	0,049	0,084
5	72	0,022	0,071
6	90	0	0,068
7	108	-0,022	0,071
8	126	-0,049	0,084
9	144	-0,094	0,116
10	162	-0,209	0,22
11	180	∞	∞

Начиная с 180⁰ значения будут повторяться по величине и знаку.

1.5 Построение линий напряжённости

Построение выполняется в соответствии с таблицей 1.2 и пунктом 1.3. Линии Е проводятся в виде дуг окружностей, пересекающихся с электрическими осями. В результате получаем полную картину поля в форме ортогональной сетки.

1.2 Определение точки с максимальной Е

1.2.1 Аналитический расчет:

в той точке, где , исследуя картину поля можно показать, что точка с максимальной Е принадлежит линии соединяющей оси и имеет координаты ; т.е. находится на поверхности левого (меньшего) цилиндра:

1.2.2 Расчет Е_max по картине поля:

При известной величине приращения потенциала, максимальное значение Е поля:

,

будет в точке .

Этому значению соответствует отрезок линии, соединяющий электрические оси, ограниченный с одной стороны следом поверхности меньшего цилиндра, с другой – соседней линией равного потенциала:

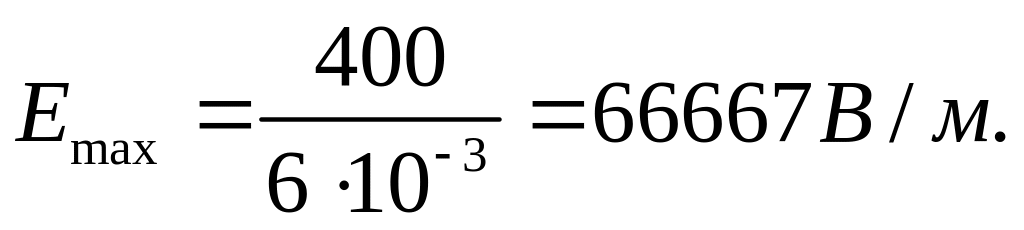
1.3 Расчет и построение кривой распределения заряда по периметру.

1.3.1 Аналитический расчет

Граничное условие для поля в диэлектрике на поверхности проводника может быть записано:

здесь .

- плотность электрического заряда на поверхности проводника;

- угол, отсчитываемый по периметру цилиндра от оси ОХ в направлении против часовой стрелки.

Величина приращения выбирается из условия:

- целое число.

В данном случае (таблица 3.1)

1.3.2 Расчет по картине поля

ΔU=U₀/10

– определяется длиной средней нормали, проведённой между линиями Е поля к поверхности цилиндра. Данные расчёта сводятся в таблицу 1.3.

По данным пунктов 1.3.1, 1.3.2. строятся кривые (рис. 3.) распределения заряда по периметру цилиндра. После построения кривых необходимо провести их анализ и сделать вывод.

Таблица 1.3 – Расчёт кривых распределения заряда

, град	, Кл/м2	, м	, Кл/м2
0	6,097	0,007	5,057
20	5,876	0,00731	4,843
40	5,319	0,00823	4,301
60	4,645	0,00968	3,657
80	4,021	0,01155	3,065
100	3,517	0,01363	2,597
120	3,147	0,01568	2,258
140	2,898	0,01742	2,032
160	2,756	0,01859	1,904
180	2,71	0,019	1,863
200	2,756	0,01859	1,904
220	2,898	0,01742	2,032
240	3,147	0,01568	2,258
260	3,517	0,01363	2,597
280	4,021	0,01155	3,065
300	4,645	0,00968	3,657
320	5,319	0,00823	4,301
340	5,876	0,00731	4,843
360	6,097	0,007	5,057

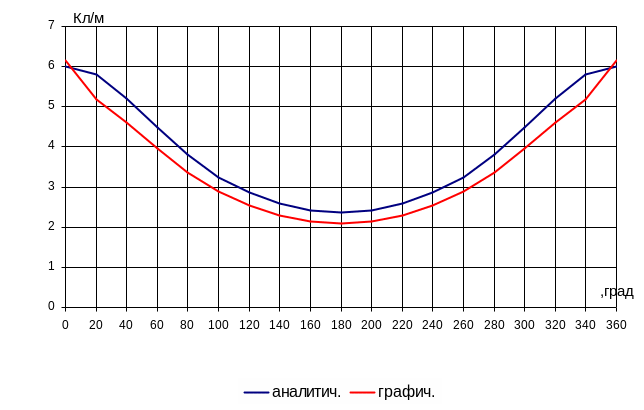Рис.3 - Кривые распределения заряда по периметру цилиндра

1.4 Расчет емкости между цилиндрами на единицу ее длины

1.4.1 Аналитический расчет

1.4.2 Расчет по картине поля

– число трубок напряженности поля;

– число эквипотенциальных промежутков;

– диаметр трубки;

– ширина промежутка.

Рис.4 – Картина поля

2 Расчет и построение магнитного поля электромагнита

Параметры катушек с ферромагнитными сердечниками могут быть определены по известной картине распределения магнитного поля, создаваемого токами , протекающими в обмотках катушек.

Точный расчет картины магнитного поля возможен для ограниченного числа случаев. Поэтому большое распространение имеют приближенные методы построения картины магнитного поля . При приближенном построении картины магнитного поля при постоянном токе обычно применяют следующие допущения :

- Магнитную проницаемость материала магнитной цепи принимают бесконечно большой;

- Картину поля рассматривают в плоскости, то есть изменением поля по одной из 3-х координат пренебрегают;

- Ширину обмоток с током принимают бесконечно малой и сечение ее считают бесконечно узким прямоугольником, расположенным непосредственно около поверхности сердечника;

В этом случае объемное распределение тока заменяется токовым слоем. При указанных допущениях картина магнитного поля в пространстве около сердечника должна удовлетворять следующим условиям:

- Линии Н везде должны пересекаться с линиями равного магнитного потенциала под прямым углом, то есть касательная к ним в точке их пересечения должна быть расположена под углом 90 градусов;

- Поверхность сердечника при отсутствии на нем обмотки с током является поверхностью равного потенциала, поэтому линии магнитной напряженности должны подходить к поверхности сердечника в областях, где нет токовых слоев, под прямым углом, то есть касательная к линии магнитной H в месте подхода линии Н к поверхности сердечника должна быть расположена под углом 90 градусов к поверхности;

- Линии равного магнитного потенциала проводятся так, чтобы приращение потенциала между соседними линиями было везде одинаковым;

- Линии магнитной напряженности проводятся таким образом, чтобы весь поток обмотки подразделялся на целое число трубок равного потока;

Линии магнитной напряженности и линии равного магнитного потенциала образуют ортогональную сетку с криволинейными прямоугольниками, у которых отношение сторон везде одинаково.

Требуется:

Провести построение и расчет картины магнитного поля электромагнита (рис. 5)

Рис.5 - Электромагнит

Первая обмотка электромагнита состоит из 2-х секций а и b, расположенных на полюсах электромагнита по обе стороны воздушного зазора и соединенных последовательно.

Вторая обмотка состоит также из 2-х катушек, расположенных на крайних стержнях ярма и также соединенных последовательно.

Полное число витков обмоток W₁ и W₂ а силы токов в них I₁ и I₂ , длина элементов в направлении, перпендикулярном чертежу – l.

Необходимо:

1) Приближенным методом построить две картины магнитного поля для случаев, когда:

а) I₁≠0 I₂=0 и б) I₁=0 I₂≠0;

Промежуток между полюсами должен быть разделен а заданное число параллельных интервалов n=8;

2) По построенной картине поля рассчитать коэффициенты самоиндукции каждой обмотки L₁ и L₂ и коэффициент взаимной индукции M . Коэффициент взаимно индукции М определить для обеих картин поля и убедиться, что М₁₂=М₂₁ ;

3) По значениям L₁, L₂ и М вычислить коэффициент связи между обмотками электромагнита и коэффициент самоиндукции цепи, состоящей из последовательно соединенных обмоток электромагнита при согласном и встречном их включении ;

4) Определить потоки и средние значения индукции в сечениях магнитной цепи, указанных на рисунке ( , и т.д.) ;

5) Найти сечение (на рисунке S₀), при котором максимальное значение индукции в ярме B=1 Тл ;

6) Построить кривую зависимости результирующей индукции в зазоре В₀ в функции X (рисунок 8);

7) Поле построить в масштабе М1:2;

8) Потоки с торцевых частей не учитывать.

Варианты заданий для второй части работы

Вар.	N cх	a, см	b, см	c, см	α, град	h, см	h΄, см	l, см	P, см	W₁ вит	W₂ вит	I₁, А	I₂, А
1	1	10	3	15	30	30	23	50	8	1000	1000	50	20
2	1	10	3,50	14,5	45	30	20	45	8	1050	1050	50	35
3	1	10	4	14	60	30	16	40	8	1100	1100	35	45
4	1	9	3	16	30	30	22	50	8	1150	950	35	40
5	1	9	3,5	16,5	45	30	19	45	8	1120	900	40	40
6	1	9	4	15	60	30	15	40	8	1250	850	40	45
7	1	8	4	16	30	30	21	50	8	1300	800	35	45
8	1	8	4,5	15,5	45	30	18	45	8	1350	750	35	50
9	1	8	3	15	60	30	14	40	8	1400	700	30	55
10	1	10	3	15	30	30	23	50	8	1200	900	40	40
11	1	10	3,5	14,5	45	30	20	45	8	1250	850	40	45
12	1	10	4	14	60	30	16	40	8	1300	800	35	45
13	1	9	3	16	30	30	22	50	8	1150	950	35	45
14	1	9	3,5	15,5	45	30	19	45	8	1350	750	35	50
15	1	9	4	15	60	30	15	40	8	1400	700	30	55
16	1	8	4	16	30	30	22	50	8	1000	1000	50	30
17	1	8	4,5	15,5	45	30	18	45	8	1050	1050	50	35
18	1	8	3	15	60	30	14	40	8	1100	1100	35	45
19	1	10	3	15	30	30	23	50	8	1050	1050	35	45
20	1	10	3,5	14,5	45	30	20	45	8	1100	1100	35	40
21	1	10	4	14	60	30	16	40	8	1150	950	40	40
22	1	9	3	16	30	30	22	50	8	1200	900	40	45
23	1	9	3,5	15,5	45	30	19	45	8	1250	850	35	45
24	1	9	4	15,5	60	30	15	40	8	1300	800	35	50
25	1	8	3	16,5	30	30	21	35	8	1350	750	30	20
26	1	8	3,5	16	45	30	18	40	8	1400	700	40	25
27	1	8	4	15,5	60	30	14	45	8	1450	900	50	30
28	1	7	5	13	30	25	14	40	8	1000	700	30	20
29	1	7	5	14	45	35	15	50	8	1100	800	45	25
30	1	7	5	15	60	25	16	40	8	1200	900	60	30

Рассмотрим построение и расчет магнитного поля электромагнита с

сердечником