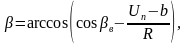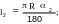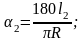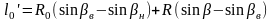3 Определение размеров стрелки
3.1 Расчет длины остряка
Наибольшее распространении в Российской Федерации получили стрелки с криволинейным остряком секущего типа. Также стрелки применяются с корневым креплением вкладышно-накладочного типа и креплением, выполненным в виде гибкого остряка. Длина гибких остряков требуется больше, так как перевод стрелки осуществляется за счет изгиба части остряка.
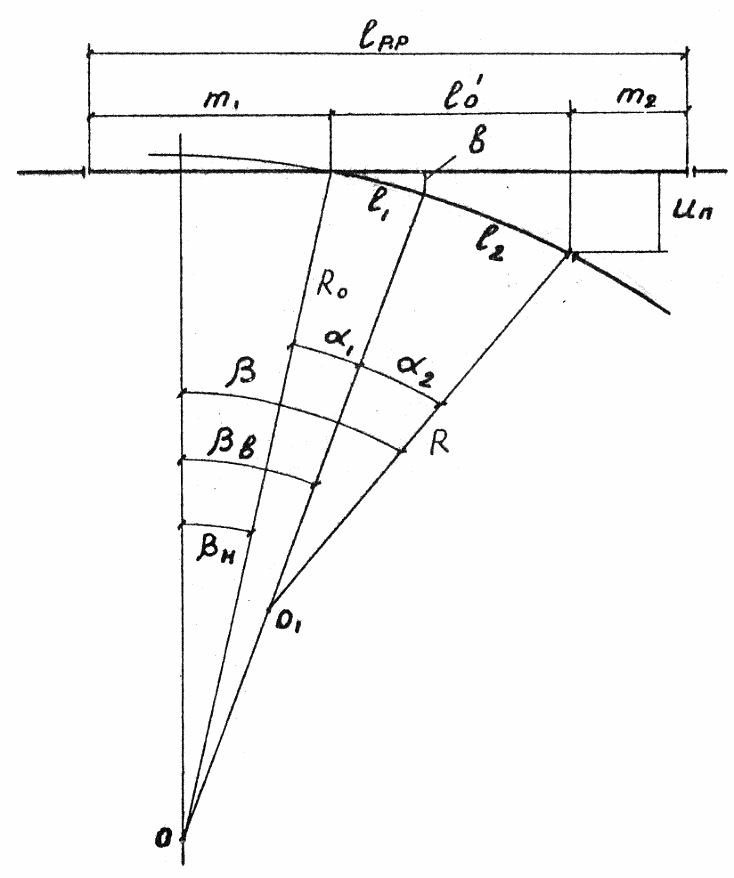
На рисунке 3.1 представлена схема взаимного расположения рабочих граней рамного рельса и криволинейного остряка.
|
На схеме приняты следующие обозначения: lP.P – длина рамного рельса; m1 – передний вылет рамного рельса; m2 – задний вылет рамного рельса; l0’ – проекция криволинейного остряка на рабочую грань рамного рельса (длина прямого остряка); R0 – радиус остряка до расчетного сечения; R – радиус переводной кривой; b – расчетное сечение; Uп – расстояние от рабочей грани рамного рельса до рабочей грани остряка в его корне; |
Рисунок 3.1 - Схема взаимного расположения рабочих граней рамного рельса и криволинейного остряка
Угол в расчетном
сечении,
,
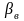определяется из выражения (3.1):
|
(3.1) |
Значение
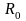и
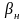определяются из графиков, из рисунка
2.4 замечаем, что
α1 = βв - βн
α2 = β - βв
α1 =
α2 =
Стрелочный угол, β, определяется по формуле (3.2):
|
(3.2) |
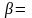
Согласно рисунку 3.1 углы α1 и α2 на дугах l1 и l2 определяются соответственно по формулам (3.3) и (3.4):
α1 = βв - βн,
|
(3.3) |
α2 = β - βв,
|
(3.4) |
α1 =
α2 =
Длина остряка определяется как сумма длин дуг l1 и l2:
|
(3.5) |
|
(3.6) |
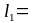
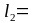
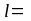
Длину остряка округляем в большую сторону и принимаем кратной 0,1 м за счет изменения длины l2.
|
(3.7) |
=
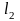Уточняем значения угла α2, стрелочного угла β и ординату в корне Uп:
|
(3.9) |
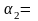
β = βв + α2;
|
(3.9) |
β =
|
(3.10) |
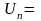
Величину проекции криволинейного остряка l'0 находим путем проектирования радиусов R0 и R на направление рабочей грани рамного рельса:
|
(3.11) |
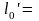
3.2 Расчет длины рамного рельса
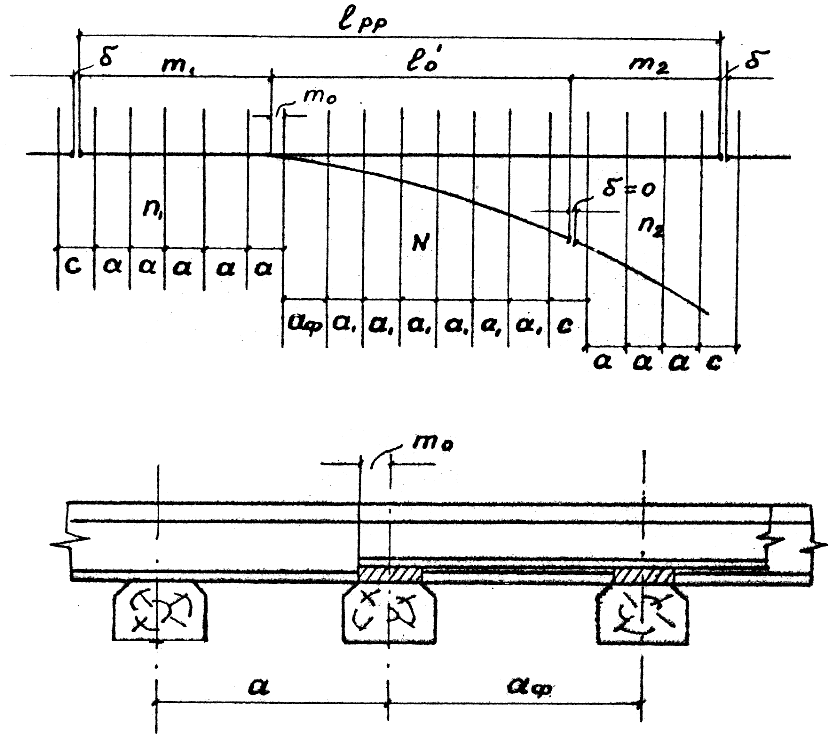
Рисунок 3.2 - Схема для расчета длин рамного рельса
Из рисунка 3.2 замечаем, что длина рамного рельса
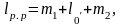
где m1 – длина переднего вылета рамного рельса;
–
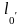проекция
криволинейного остряка на направление
рабочей грани рамного рельса;
m2 – длина заднего вылета рамного рельса.
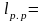
Определим передний и задний вылет рамного рельса из условия раскладки брусьев:
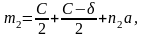
где С – стыковой пролет, принимается в зависимости от типа верхнего строения пути;
n1 – число ящиков в переднем вылете рамного рельса m1, принимаемое от 3 до 9;
n2 – число ящиков в заднем вылете рамного рельса m2, принимаемое от 2 до 10;
δ – стыковой зазор, равный 8 - 10 мм;
m0 – забег остряка за ось флюгарочного бруса, принимается равным 41 мм - половине ширины стрелочной подушки;
а – ширина ящиков под передним и задним вылетами рамного рельса, принимается в пределах 500 - 550 мм.
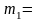
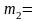
Длина рамного рельса, полученная по формуле, округляется в большую сторону и принимается равной 12,50; 18,75; 25,00 м за счет изменения заднего вылета рамного рельса m2.
m2 = 12500 - m1 - l'0;
m2 = 18750 - m1 - l'0;
m2 = 25000 - m1 - l'0.
m2 =
Для определения числа ящиков под остряком запишем следующее выражение:
l'0 = m0 + aф + Na1 +0,5∙С,
где аф – флюгарочный пролет, берется в пределах 600...700 мм;
N - число пролетов под остряком;
а1 - расстояние между осями брусьев под остряком;
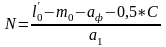
Принимается целое число пролетов. Расстояние между осями брусьев устанавливается кратными 5 мм, один пролет может получиться не кратным 5 мм.
Стыки в переднем, заднем вылетах рамного рельса и корне остряка устраиваются на весу со стандартным пролетом С.