Введение в теорию вероятностей часть 2

Вариант 15

1. ДСВ задана законом распределения: . Найти вероятность Р, построить многоугольник распределения и функцию распределения.

2. В условиях задачи 1 определить моду, математическое ожидание, дисперсию и среднеквадратичное отклонение ДСВ Х.

3. В урне находятся 3 белых и 7 черных шаров. Наудачу отобраны два шара. Найти математическое ожидание и дисперсию ДСВ = число белых шаров

4. Задана плотность распределения нсв х . Найти постоянную с, функцию распределения и вероятность выполнения неравенства .

5. В условиях задачи 4 определить начальные и центральные моменты НСВ первого и второго порядка.

6. НСВ Х распределена по стандартному закону. Определить вероятность выполнения неравенства .

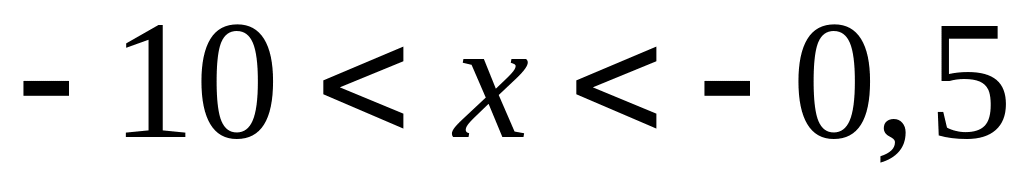7. В условиях задачи 6 найти длину интервала, симметричного относительно математического ожидания, в который с вероятностью 0, 9973 попадет НСВ Х в результате испытания.

8. НСВ Х распределена по показательному закону с параметром 2. Найти вероятность того, что в результате испытания НСВ Х примет значение, лежащее на интервале (0,15 ; 0,65)

9. ДСВ Х имеет характеристики . Оценить снизу вероятность события .

10. Задана функция распределения двумерной СВ: 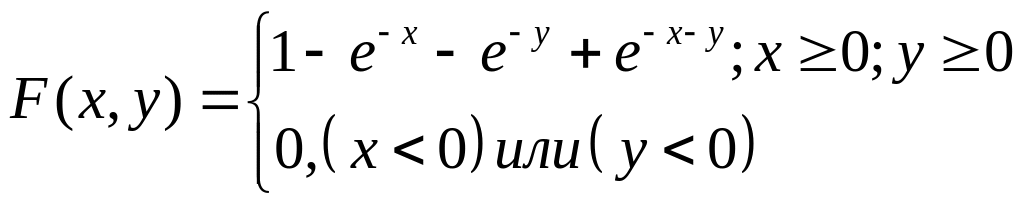. Найти двумерную плотность распределения вероятности системы.

Введение в теорию вероятностей часть 2

Вариант 16

1. По цели производится три независимых выстрела. Вероятность попадания в цель при каждом выстреле равна 0,5. Получить закон распределения числа попаданий, построить полигон распределения и график функции распределения.

2. В условиях задачи 1 определить моду, математическое ожидание, дисперсию и среднеквадратичное отклонение ДСВ = число попаданий

3. Брошены игральных костей. Найти дисперсию суммы числа очков, которые могут выпасть на всех выпавших гранях.

4. Плотность распределения НСВ Х задана на всей оси Ох равенством 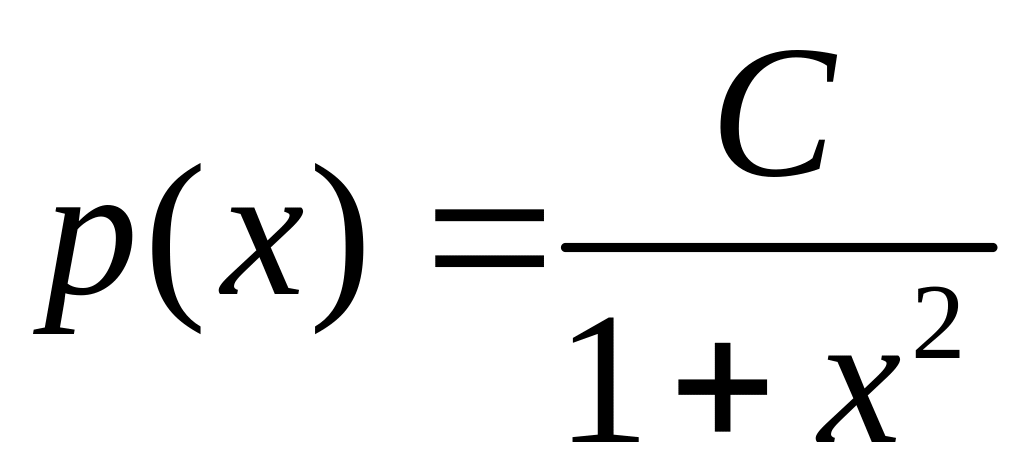. Найти постоянную С, функцию распределения и вероятность выполнения неравенства .

5. Задана плотность распределения НСВ Х . Определить медиану, начальные и центральные моменты НСВ первого и второго порядка.

6. Производится взвешивание некоторого вещества без систематических ошибок. Случайные ошибки взвешивания подчинены нормальному закону со среднеквадратичным отклонением 10г. Найти вероятность того, что взвешивание будет произведено с ошибкой, не превосходящей по абсолютной величине 5г.

7. НСВ Х распределена по нормальному закону с параметрами 70 ; 5. Определить вероятность того, что в результате опыта НСВ Х примет значение, большее 83.

8. НСВ Х распределена по показательному закону с параметром 0,03. Найти вероятность того, что в результате испытания НСВ Х попадет в интервал (3 ; 7).

9. Вероятность появления события А в каждом испытании равно 0,3. Пользуясь неравенством Чебышева, оценить вероятность того, что число появлений события А будет заключено в пределах от 25 до 35, если будет произведено 100 независимых испытаний.

10. В кольце двумерная плотность вероятности ; вне кольца =0. найти постоянную С.