Введение в теорию вероятностей часть 2

Вариант 13

1. В урне находятся 3 белых и 2 черных шара. Наудачу отобраны два шара. Составить закон распределения числа белых шаров среди отобранных шаров. Построить график функции распределения.

2. В условиях задачи 1 определить моду, математическое ожидание, дисперсию и среднеквадратичное отклонение ДСВ = число белых шаров

3. Студенту М. задают на экзамене дополнительные вопросы. Вероятность ответить на вопрос постоянна и равна 0,7. Экзаменатор прекращает задавать вопросы тогда, когда студент Н. не отвечает. Определить математическое ожидание ДСВ = число заданных вопросов . Вычислить вероятность того, что студент Н. не ответит уже на второй вопрос.

4. Плотность распределения НСВ задана выражением: Найти значение параметра , функцию распределения и вероятность выполнения неравенства .

5. В условиях задачи 4 определить моду, математическое ожидание, дисперсию и среднеквадратичное отклонение НСВ .

6. Производится взвешивание некоторого вещества без систематических ошибок. Случайные ошибки взвешивания подчинены нормальному закону со среднеквадратичным отклонением г. Найти вероятность того, что взвешивание будет произведено с ошибкой, не превосходящей по абсолютной величине 10г.

7. НСВ Х распределена по нормальному закону с параметрами 20 ; 2. Определить вероятность того, что в результате опыта НСВ Х примет значение, большее 25.

8. НСВ Х распределена по показательному закону с параметром 1,5. Найти вероятность того, что в результате испытания НСВ Х попадет в интервал (0,5 ; 2,5).

9. В сеть освещения параллельно включены 20 светодиодов. Вероятность того, что за время Т светодиод включится, равна 0,8. С помощью неравенства Чебышева оценить вероятность того, что абсолютная величина разности между числом включенных светодиодов и средним числом включенных светодиодов за время Т окажется не меньше трех.

10. Задана функция распределения двумерной СВ: . Найти двумерную плотность распределения вероятности системы.

Введение в теорию вероятностей часть 2

Вариант 14

1. ДСВ задана законом распределения: . Найти вероятность Р, построить функцию распределения, определить вероятность того, что ДСВ Х примет отрицательное значение.

2. В условиях задачи 1 определить моду, математическое ожидание, дисперсию и среднеквадратичное отклонение ДСВ Х.

3. Брошены игральных костей. Найти математическое ожидание суммы числа очков, которые выпадут на всех костях.

4. Задана плотность распределения нсв х . Найти постоянную с, функцию распределения и вероятность выполнения неравенства .

5. Задана плотность распределения НСВ Х 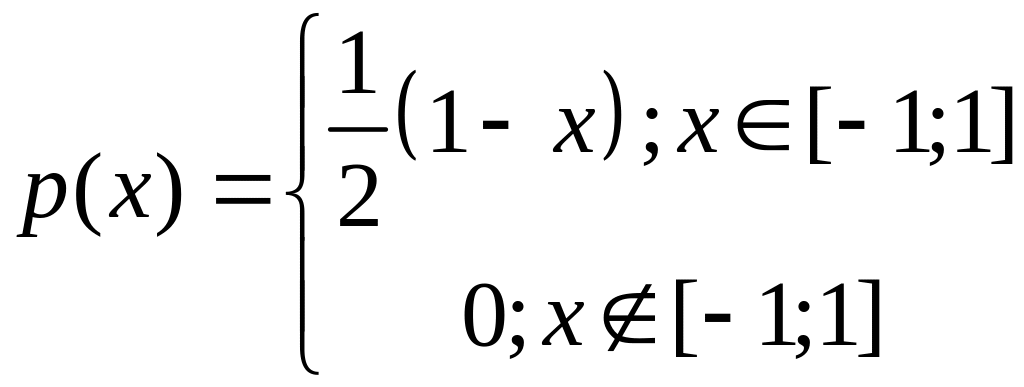. Определить моду, математическое ожидание, дисперсию и среднеквадратичное отклонение НСВ.

6. По данным М-ского военкомата рост призывников распределен по нормальному закону с математическим ожиданием 178 см. и дисперсией 6 см. Определить вероятность того. что рост наудачу выбранного призывника отклонится от математического ожидания менее чем на 10 см.

7. НСВ Х распределена по нормальному закону с параметрами 65 ; 3. Определить вероятность того, что в результате опыта НСВ Х примет значение, меньшее 52.

8. НСВ Х распределена по показательному закону с параметром 0,08. Найти вероятность того, что в результате испытания НСВ Х попадет в интервал (2 ; 6).

9. Вероятность появления события А в каждом испытании равно 0,5. Пользуясь неравенством Чебышева, оценить вероятность того, что число появлений события А будет заключено в пределах от 80 до 120, если будет произведено 200 независимых испытаний.

10. Задана плотность распределения двумерной СВ: . Найти постоянную С.

;