Введение в теорию вероятностей часть 2

Вариант 9

1. Брошены две одинаковые игральные кости. ДСВ - число появлений пяти очков. Получить закон распределения ДСВ. Построить график функции распределения.

2. В условиях задачи 1 определить моду, математическое ожидание, дисперсию и среднеквадратичное отклонение ДСВ = число появлений пяти очков

3. Студенту М. задают на экзамене дополнительные вопросы. Вероятность ответить на вопрос постоянна и равна 0,8. Экзаменатор прекращает задавать вопросы тогда, когда студент М. не отвечает. Определить математическое ожидание ДСВ = число заданных вопросов . Определить вероятность того, что студент М. не ответит на третий вопрос.

4. Плотность распределения НСВ задана выражением: Найти значение параметра , функцию распределения и вероятность выполнения неравенства .

5. В условиях задачи 4 определить моду, математическое ожидание, дисперсию и среднеквадратичное отклонение нсв х.

6. НСВ Х распределена по стандартному закону. Определить вероятность выполнения неравенства .

7. В условиях задачи 6 найти длину интервала, симметричного относительно математического ожидания, в который с вероятностью 0, 994 попадет НСВ Х в результате испытания.

8. НСВ Х распределена по показательному закону с параметром 0,02. Найти вероятность того, что в результате испытания НСВ Х примет значение, меньшее 6.

9. Пусть в результате 100 независимых испытаний найдены значения случайной величины : 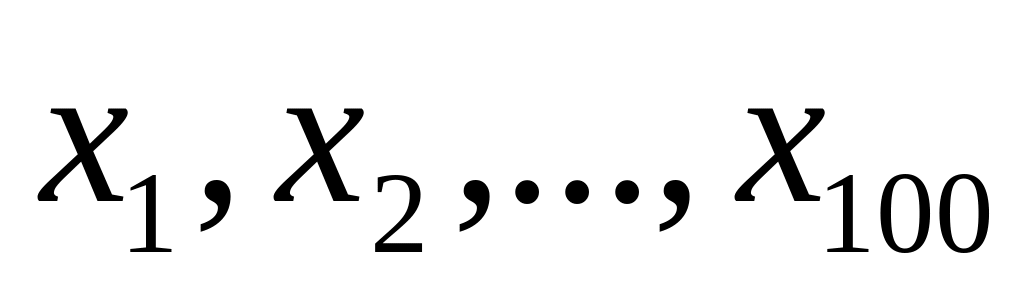. Пусть математическое ожидание 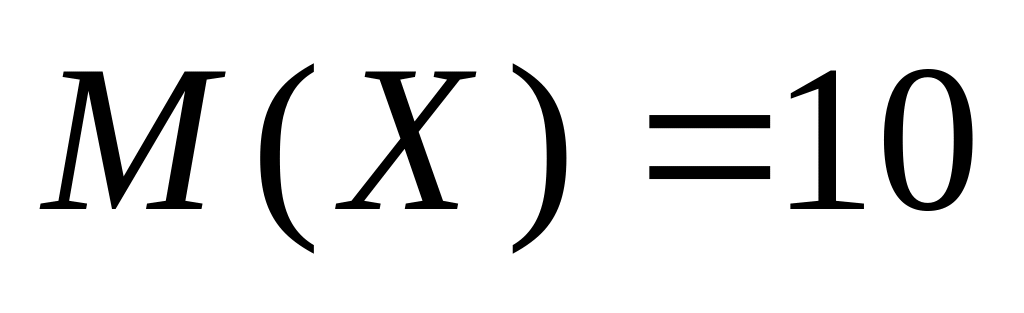, а дисперсия . Оценить вероятность того, что абсолютная величина разности между средним арифметическим наблюдаемых значений случайной величины и ее математическим ожиданием будет меньше 0,5.

10. В кольце двумерная плотность вероятности 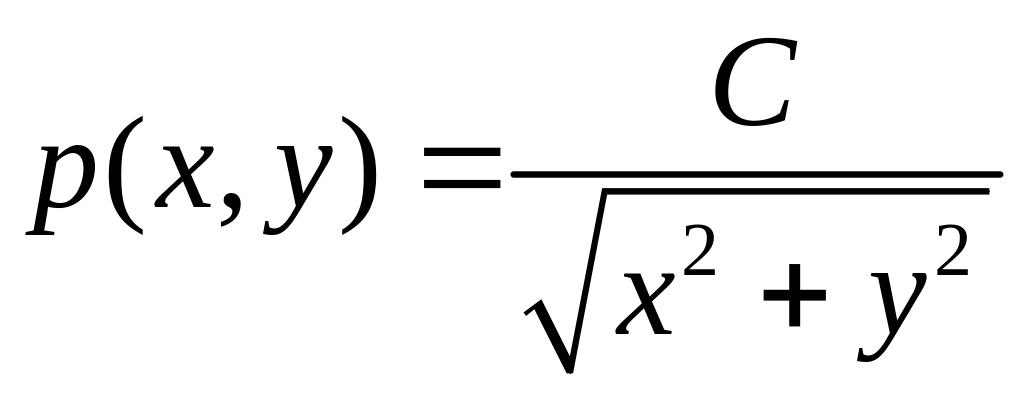; вне кольца =0. найти постоянную С.

Введение в теорию вероятностей часть 2

Вариант 10

1. Опыт состоит из двух независимых бросаний монеты. Для случайного числа появлений герба получить закон распределения, построить многоугольник распределения и график функции распределения.

2. В условиях задачи 1 определить моду, математическое ожидание, дисперсию и среднеквадратичное отклонение ДСВ = число появлений герба

3. ДСВ и независимы. Известно, что , , ; . Найти математическое ожидание и дисперсию ДСВ .

4. Задана плотность распределения нсв х . Найти постоянную с, функцию распределения и вероятность выполнения неравенства .

5. В условиях задачи 4 определить моду, математическое ожидание, дисперсию и среднеквадратичное отклонение нсв х.

6. По данным Н-ского военкомата рост призывников распределен по нормальному закону с математическим ожиданием 180 см. и дисперсией 8 см. Определить вероятность того. что рост наудачу выбранного призывника не отклонится от математического ожидания более чем на 15 см.

7. Автомат штампует детали. Контролируется длина детали Х, которая распределена нормально с математическим ожиданием 50 мм. Фактически длина изготовленных деталей не менее 32 мм и не более 68 мм. Найти вероятность того, что длина наудачу взятой детали будет меньше 40 мм.

8. НСВ Х распределена по показательному закону с параметром 0,1. Найти вероятность того, что в результате испытания НСВ Х примет значение, большее 5.

9. Вероятность того, что деталь бракованная, равна 0,05. Пусть СВ Х - число бракованных деталей в партии из 10 деталей. С помощью неравенства Чебышева оценить вероятность того, что абсолютная величина разности между Х и окажется меньше двух.

10. Задан закон распределения двумерной ДСВ. Установить, зависимы ли компоненты и .