Введение в теорию вероятностей часть 2
Вариант 7
Дискретная случайная величина задана законом распределения:
.
Найти вероятность Р, построить
многоугольник распределения и график
функции распределения.В условиях задачи 1 определить моду, математическое ожидание, дисперсию и среднеквадратичное отклонение ДСВ Х.
ДСВ
,
,
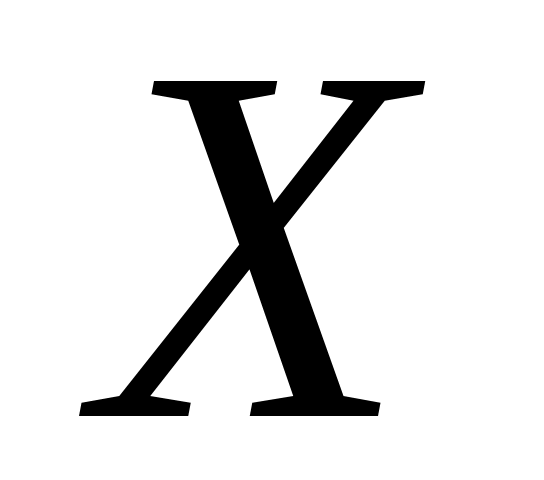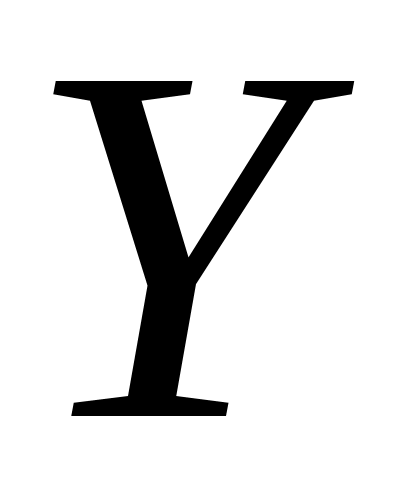независимы. Известно, что
,
,
,
;
;
.
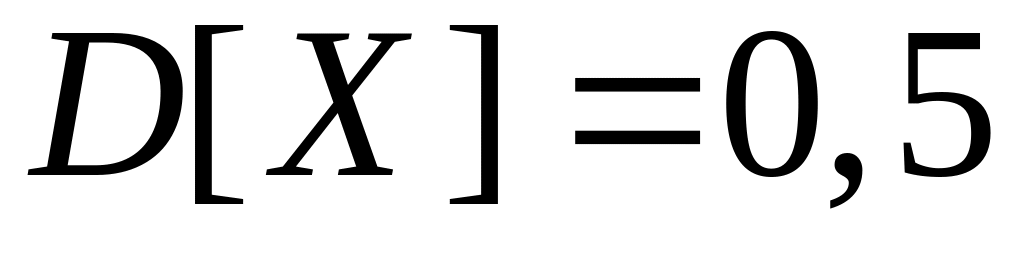Найти математическое ожидание и
дисперсию ДСВ
.
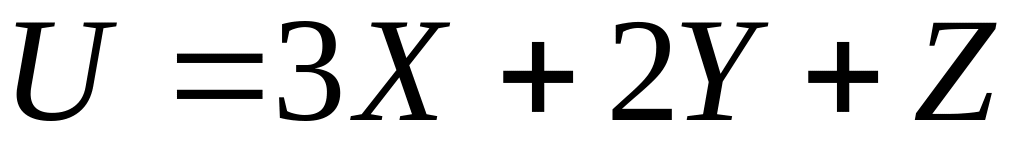Задана плотность распределения нсв х . Найти постоянную с, функцию распределения и вероятность выполнения неравенства .
В условиях задачи 4 определить моду, математическое ожидание, дисперсию и среднеквадратичное отклонение нсв х.
Ошибка радиодальномера подчинена нормальному закону. Математическое ожидание этой ошибки равна 2,5 м, а среднее квадратичное отклонение 5 м. Найти вероятность того, что измеренное расстояние будет отклоняться от истинного не более, чем на 10 м.
НСВ Х распределена нормально с математическим ожиданием
.
Вероятность попадания Х в интервал
(15;25) равна 0,30. Чему равна вероятность
попадания Х в интервал (5;15)?
НСВ Х распределена по показательному закону с параметром 0,1. Найти вероятность того, что в результате испытания НСВ Х примет значение, меньшее 3.
Распределение случайной величины задано следующей таблицей:
.
Чему равна вероятность того, что
?
Оценить эту вероятность, пользуясь
неравенством Чебышева.
Задан закон распределения двумерной ДСВ. Вычислить вероятность события А=
Введение в теорию вероятностей часть 2
Вариант 8
Опыт состоит из трех независимых бросаний монеты. Для случайного числа появлений герба получить закон распределения, построить многоугольник распределения и график функции распределения.
В условиях задачи 1 определить моду, математическое ожидание, дисперсию и среднеквадратичное отклонение ДСВ = число появлений герба
ДСВ Х распределена по закону Пуассона с параметром
.
Определить вероятность того, что ДСВ
Х примет значение от 1 до 3.
Задана плотность распределения нсв х . Найти постоянную с, функцию распределения и вероятность выполнения неравенства .
В условиях задачи 4 определить начальные и центральные моменты первого и второго порядка НСВ Х.
НСВ Х распределена по нормальному закону с параметрами
.
Определить вероятность выполнения
неравенства
.
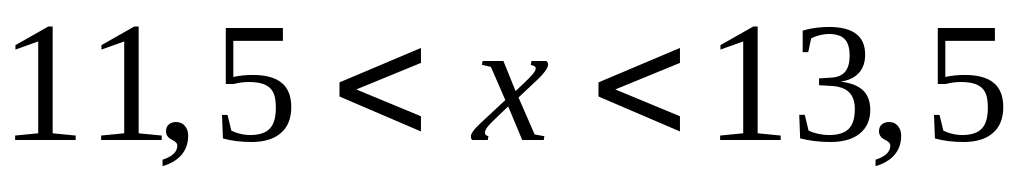В условиях задачи 6 найти длину интервала, симметричного относительно математического ожидания, в который с вероятностью 0, 984 попадет НСВ Х в результате испытания.
НСВ Х распределена по показательному закону с параметром 5. Найти вероятность того, что в результате испытания НСВ Х примет значение, лежащее на интервале (0,05 ; 0,50).
Вероятность появления события в каждом испытании равна 0,25. Пользуясь неравенством Чебышева, оценить вероятность того, что число появлений события будет заключено в пределах от 150 до 250, если будет произведено 800 испытаний.
Задан закон распределения двумерной ДСВ. . Установить, зависимы ли компоненты и
.