Введение в теорию вероятностей часть 2

Вариант 5

1. Брошены две одинаковые игральные кости. ДСВ - число появлений шести очков. Получить закон распределения ДСВ. Построить график функции распределения.

2. В условиях задачи 1 определить моду, математическое ожидание, дисперсию и среднеквадратичное отклонение ДСВ = число появлений шести очков

3. Вероятность наступления события А в одном испытании равна 0,3. Опыт повторяют до наступления события А. Определить математическое ожидание ДСВ = число повторений опыта . Вычислить вероятность того, что А наступит в третьем испытании.

4. Задана плотность распределения нсв х . Найти постоянную с, функцию распределения и вероятность выполнения неравенства .

5. В условиях задачи 4 определить моду, математическое ожидание, дисперсию и среднеквадратичное отклонение нсв х.

6. НСВ Х распределена по нормальному закону с параметрами . Определить вероятность выполнения неравенства .

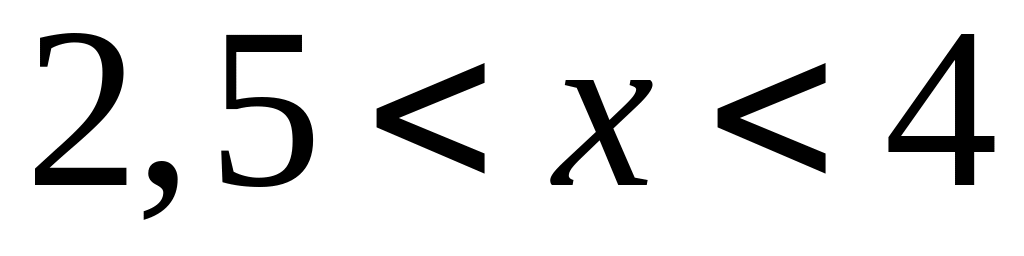7. В условиях задачи 6 найти длину интервала, симметричного относительно математического ожидания, в который с вероятностью 0, 9975 попадет НСВ Х в результате испытания.

8. НСВ Х распределена по показательному закону с параметром 2. Найти вероятность того, что в результате испытания НСВ Х примет значение, лежащее на интервале (0,1 ; 0,8).

9. Среднее значение длины детали – 50 см. Дисперсия равна 0,1. Пользуясь неравенством Чебышева, оценить вероятность того, что случайно взятая деталь окажется по длине не менее 49,5 см и не более 50,5 см.

10. Задан закон распределения двумерной ДСВ. Вычислить вероятность события В=

Введение в теорию вероятностей часть 2

Вариант 6

1. По цели производится два независимых выстрела. Вероятность попадания в цель при каждом выстреле равна 0,5. Получить закон распределения числа попаданий, построить полигон распределения и график функции распределения.

2. В условиях задачи 1 определить моду, математическое ожидание, дисперсию и среднеквадратичное отклонение ДСВ = число попаданий

3. Испытания образца композита на прочность проводятся до разрушения образца. Вероятность разрушения образца в каждом испытании равна 0,2. Определить математическое ожидание ДСВ = число испытаний . Вычислить вероятность того, что образец разрушится при третьем испытании.

4. Задана плотность распределения нсв х . Найти постоянную с, функцию распределения и вероятность выполнения неравенства .

5. Задана плотность распределения НСВ Х . Определить моду, математическое ожидание, дисперсию и среднеквадратичное отклонение НСВ Х.

6. Найти вероятность того, что нормальная случайная величина Х с математическим ожиданием, равным нулю, и дисперсией, равной четырем, примет значение, меньшее нуля, но большее (– 6) .

7. В условиях задачи 6 найти длину интервала, симметричного относительно математического ожидания, в который с вероятностью 0, 995 попадет нсв х в результате испытания.

8. НСВ Х распределена по показательному закону с параметром 0,1. Найти вероятность того, что в результате испытания НСВ Х примет значение, большее 1.

9. Вероятность появления события А в каждом испытании равно 0,5. Пользуясь неравенством Чебышева, оценить вероятность того, что число появлений события А будет заключено в пределах от 40 до 60, если будет произведено 100 независимых испытаний.

10. Задан закон распределения двумерной ДСВ. 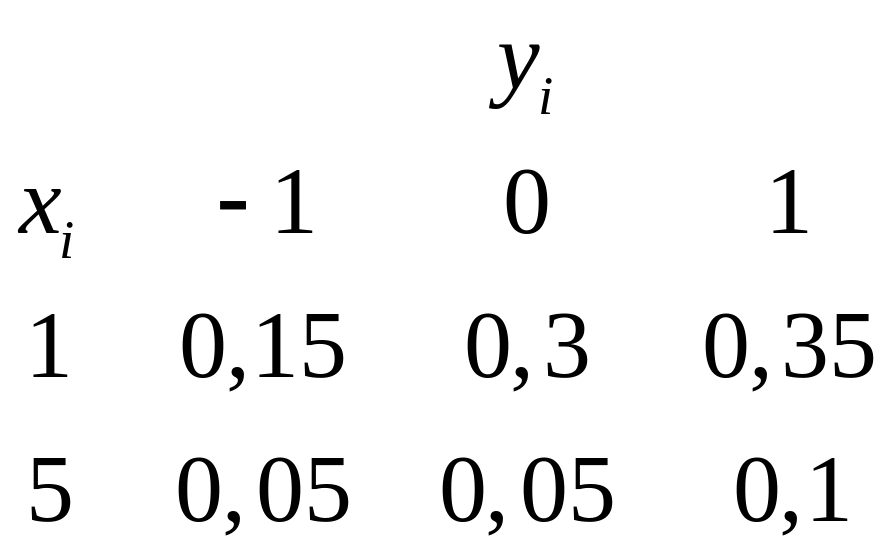. Вычислить вероятность события А=