Введение в теорию вероятностей часть 2
Вариант 23
Получить закон распределения для числа мальчиков в семье с двумя детьми, считая вероятности рождения мальчика и девочки одинаковыми. Построить полигон распределения и график функции распределения.
В условиях задачи 1 определить моду, математическое ожидание, дисперсию и среднеквадратичное отклонение ДСВ = число мальчиков
Испытывается устройство, состоящее из трех независимо работающих приборов. Вероятности отказа приборов таковы:
,
,
.
Найти математическое ожидание числа
отказавших приборов.
Задана плотность распределения нсв х . Найти постоянную с, функцию распределения и вероятность выполнения неравенства
В условиях задачи 4 определить моду, математическое ожидание, дисперсию и среднеквадратичное отклонение НСВ.
Математическое ожидание и среднеквадратичное отклонение нормально распределенной случайной величины Х соответственно равны 20 и 5. Найти вероятность того, что в результате испытания случайная величина примет значение, заключенное в интервале (15 ; 25).
В условиях задачи 6 найти длину интервала, симметричного относительно математического ожидания, в который с вероятностью 0, 9950 попадет НСВ Х в результате испытания.
Нсв х распределена по показательному закону с параметром 0,6. Найти вероятность того, что в результате испытания нсв х примет значение, лежащее на интервале (1 ; 4).
ДСВ Х- число солнечных дней в году для данной местности. Установлено, что = 100 дней,
=
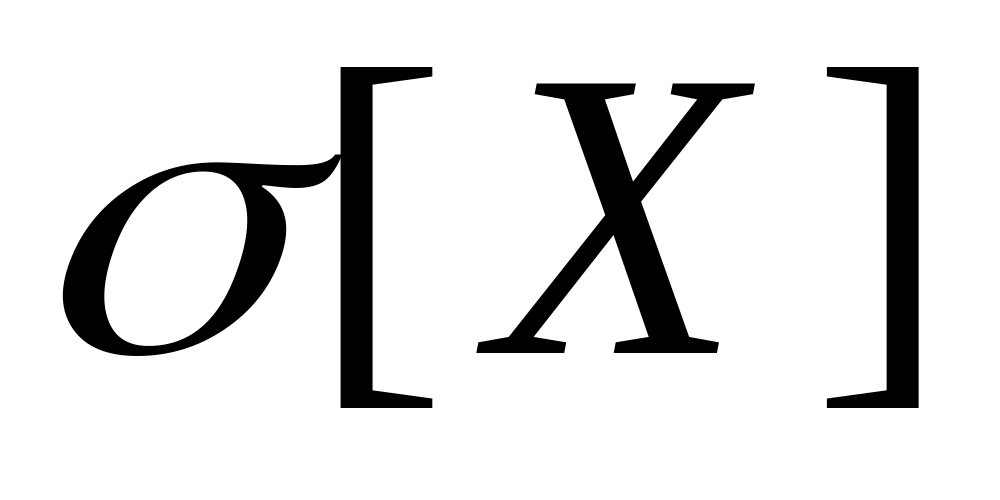20 дней. Оценить сверху вероятность
события
.
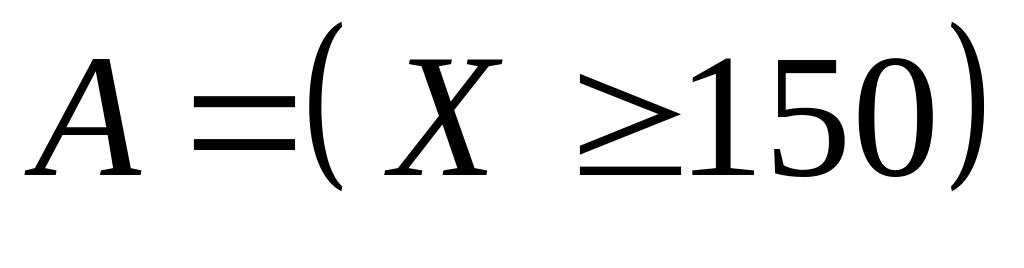В первом квадранте задана двумерная плотность распределения вероятности системы двух СВ:
;
вне квадранта
.
Найти вероятность попадания случайной
точки
в прямоугольник
.
Введение в теорию вероятностей часть 2
Вариант 24
ДСВ задана законом распределения:
.
Найти вероятность Р, построить график
функции распределения, определить
вероятность того, что ДСВ Х примет
значение, меньшее 0,25.В условиях задачи 1 определить моду, математическое ожидание, дисперсию и среднеквадратичное отклонение ДСВ Х.
Вероятность наступления события А в одном испытании равна 0,4. Опыт повторяют до наступления события А. Определить математическое ожидание ДСВ = число повторений опыта . Вычислить вероятность того, что А наступит во втором опыте.
Задана плотность распределения нсв х . Найти постоянную с, функцию распределения и вероятность выполнения неравенства .
Задана плотность распределения НСВ Х
.
Определить медиану, начальные и
центральные моменты НСВ первого и
второго порядка.
НСВ Х распределена стандартным образом. Определить вероятность выполнения неравенства
.
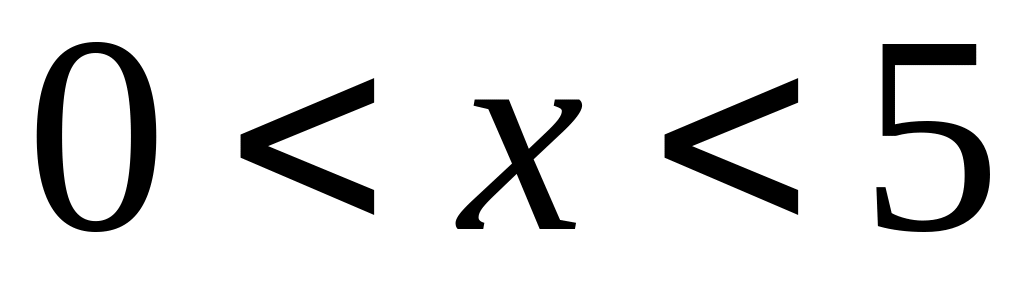В условиях задачи 6 найти длину интервала, симметричного относительно математического ожидания, в который с вероятностью 0, 9980 попадет НСВ Х в результате испытания.
НСВ Х распределена по показательному закону с параметром 0,6. Найти вероятность того, что в результате испытания НСВ Х примет значение, лежащее на отрезке
.
ДСВ Х- число солнечных дней в году для данной местности. Установлено, что = 100 дней, = 20 дней. Оценить сверху вероятность события
.
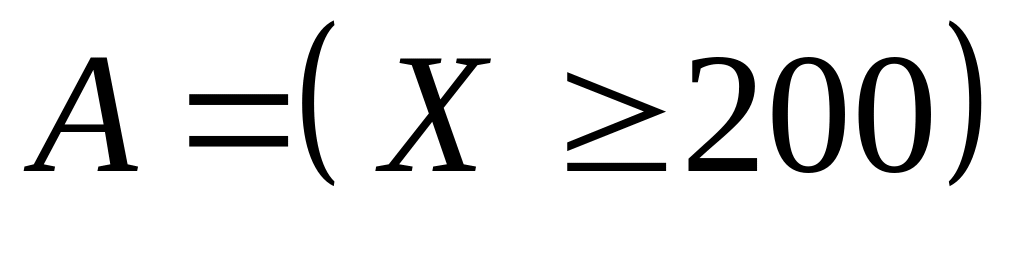В квадрате задана двумерная плотность вероятности системы двух СВ:
;
вне квадрата
.
Найти вероятность попадания точки
в квадрат
.