Введение в теорию вероятностей часть 2

Вариант 1

1. По цели производится два независимых выстрела. Вероятность попадания в цель при каждом выстреле равна 0,4. Получить закон распределения числа попаданий, построить полигон распределения и график функции распределения.

2. В условиях задачи 1 определить моду, математическое ожидание, дисперсию и среднеквадратичное отклонение ДСВ = число попаданий

3. Вероятность наступления события А в одном испытании равна 0,4. Опыт повторяют до наступления события А. Определить математическое ожидание ДСВ = число повторений опыта . Вычислить вероятность того, что А наступит во втором опыте.

4. Задана плотность распределения НСВ Х: . Найти постоянную С, функцию распределения и вероятность выполнения неравенства

5. В условиях задачи 4 определить моду, математическое ожидание, дисперсию и среднеквадратичное отклонение НСВ Х.

6. Математическое ожидание и среднеквадратичное отклонение нормально распределенной случайной величины Х соответственно равны 10 и 2. Найти вероятность того, что в результате испытания случайная величина примет значение, заключенное в интервале (12 ; 14).

7. В условиях задачи 6 найти длину интервала, симметричного относительно математического ожидания, в который с вероятностью 0, 997 попадет НСВ Х в результате испытания.

8. Студент помнит, что плотность показательного распределения вроде бы имеет вид 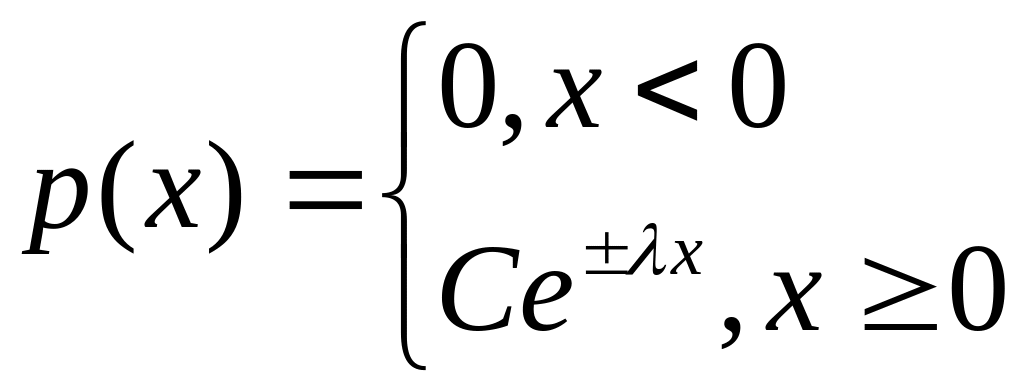, однако забыл, чему равно С и понимает, что вместо нужно выбрать какой-то один знак. Как решить эти два вопроса?

9. ДСВ задана законом распределения: Пользуясь неравенством Чебышева, оценить вероятность того, что .

10. Задан закон распределения двумерной ДСВ. Найти безусловные законы распределения составляющих и

Введение в теорию вероятностей часть 2

Вариант 2

1. В урне находятся 8 белых и два черных шара. Наудачу отобраны два шара. Составить закон распределения числа белых шаров среди отобранных шаров. Построить график функции распределения.

2. В условиях задачи 1 определить моду, математическое ожидание, дисперсию и среднеквадратичное отклонение ДСВ = число белых шаров

3. ДСВ Х распределена по закону Пуассона с параметром . Определить вероятность того, что ДСВ Х примет значение, не превышающее к=3.

4. Задана плотность распределения НСВ Х 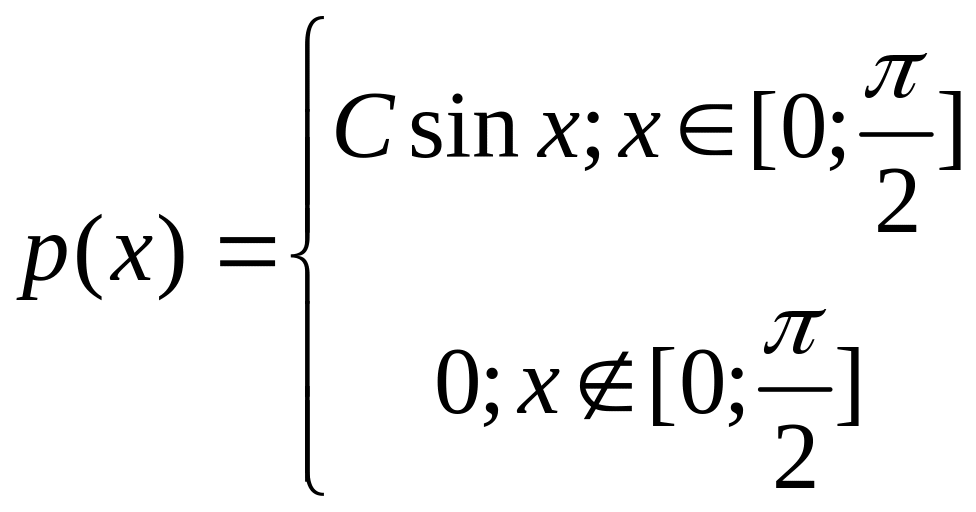. Найти постоянную С, функцию распределения и вероятность выполнения неравенства .

5. В условиях задачи 4 определить моду, математическое ожидание, дисперсию и среднеквадратичное отклонение нсв х.

6. Ошибка радиодальномера подчинена нормальному закону.

Математическое ожидание этой ошибки равна 5 м, а среднее квадратичное отклонение – 10 м. Найти вероятность того, что измеренное расстояние будет отклоняться от истинного не более, чем на 20 м.

7. НСВ Х распределена нормально с математическим ожиданием . Вероятность попадания Х в интервал (10;20) равна 0,25. Чему равна вероятность попадания Х в интервал (0;10)?

8. НСВ Х распределена по показательному закону с параметром 3. Найти вероятность того, что в результате испытания НСВ Х примет значение, лежащее на интервале (0,1 ; 0,7).

9. Вероятность появления события в каждом испытании равна 0,25. Пользуясь неравенством Чебышева, оценить вероятность того, что число появлений события будет заключено в пределах от 150 до 250, если будет проведено 800 испытаний.

10. Задан закон распределения двумерной ДСВ. 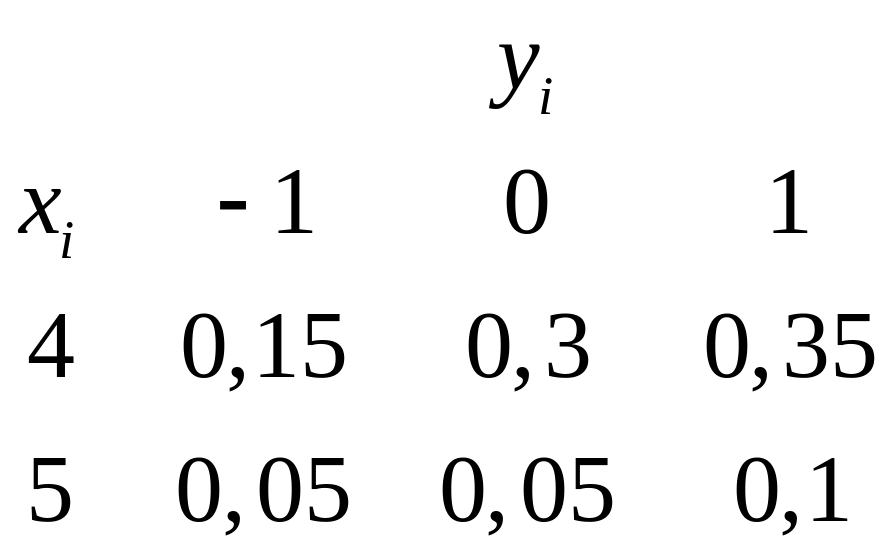Найти безусловные законы распределения составляющих и