4.4. Аппроксимация начальных и граничных условий

Условия представим в разностном виде.

1. Начальное условие

соответствует нижнему ряду точек на разностной сетке, в разностном виде:

j=0, 1, … , I.

2. Граничные условия 1-го рода

соответствует крайнему слева ряду точек на разностной сетке; левая часть правого граничного условия – крайнему справа ряду точек, в разностном виде:

(2.20)

где n = 0, 1, … , N.

3. Граничные условия 2-го рода

в некоторой точке t ⁿ аппроксимируются в разностном виде соответственно:

(2.22)

4. Граничные условия 3-го рода в общем виде

в некоторой точке t ⁿ аппроксимируются конечными разностями на разностной сетке в разностном виде:

(2.23)

5. Спектральный (гармонический) метод анализа устойчивости разностных схем

5. 1. Устойчивость разностных схем

При численном решении дифференциальных уравнений неизбежно возникают два типа источников этих ошибок:

- сама аппроксимация, т.е. замена производных в исходных дифференциальных уравнениях конечными разностями;

- погрешность вычислений.

Ошибки могут возникать при неточности вычислений, как самой разностной схемы, так и начальных и граничных условий. Если в ошибки не возрастают, то разностная схема устойчива, если же возрастают, то – неустойчива.

Запишем дифференциальную краевую задачу в виде символьного равенства:

L u = f, (3.1)

где L – дифференциальный оператор; u – искомая функция; f – правая часть дифференциального уравнения.

Тогда разностную схему кратко можно представить в следующем виде:

(3.2)

где L_h – разностный оператор, действующий на сеточную функцию u^(h), являющуюся результатом решения разностной задачи; – проекция на разностную сетку непрерывной функции f.

Понятие нормы функции u(x _j):

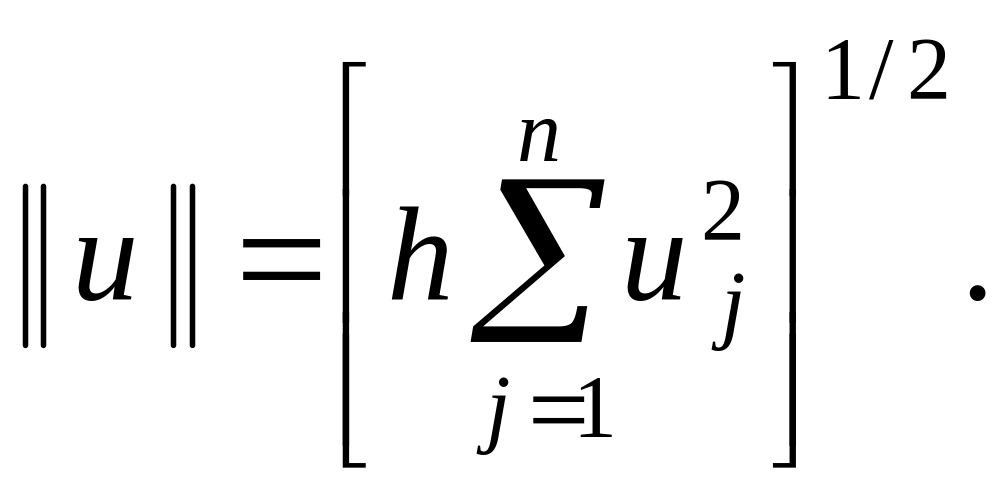
Теорема 1. Разностная схема (3.2) с линейным оператором L_h устойчива, если при любом уравнение (3.2) имеет единственное решение , причём где с – константа, U_h – множество решений, F_h – множество правых частей.

Теорема 2. Пусть разностная схема (3.2) аппроксимирует дифференциальное уравнение (3.1) с порядком аппроксимации и является устойчивой. Тогда решение разностной задачи (3.2) u^(h) сходится к решению исходной дифференциальной задачи (3.1) [u]_h и имеет место неравенство:

где М – константа.

Таким образом, сходимость решения разностной схемы к решению исходного уравнения имеет место только при выполнении двух требований:

1) разностная схема должна аппроксимировать исходное уравнение;

2) разностная схема должна быть устойчива.

5.2. Необходимое условие устойчивости разностных схем

Для дифференциального уравнения параболического типа (свободный член которого не включает искомую функцию u:

(3.3)

Явная разностная схема:

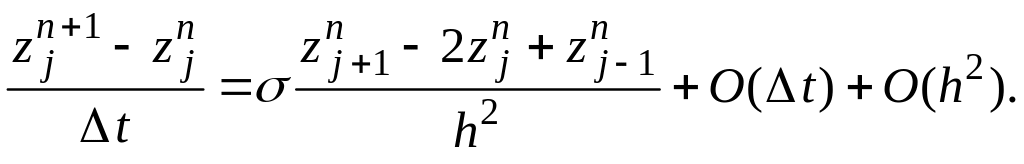(3.4)

имеет погрешность аппроксимации .

Выразим из соотношения (3.4):

Последний член в правой части полученного выражения имеет порядок малости, явно меньший t, что позволяет им пренебречь, т.о.:

или в операторном виде:

Здесь zⁿ – вектор погрешностей, Е – единичный оператор:

Оператор - оператор перехода по времени от п-го шага к (n + 1)-му шагу.

Согласно определению устойчивости разностных схем, необходимо, чтобы норма погрешности на (n + 1)-ом шаге по времени не превосходила нормы погрешности на п-ом шаге по времени, то есть:

(3.6)

Погрешность решения разностной схемы в точке можно представить в виде комплексного выражения (гармоники):

(3.7)

где  – собственное число оператора перехода В; i – мнимая единица.

Теорема. Для того, чтобы разностная схема была устойчива (т.е. для выполнения условия (3.6)), необходимо, чтобы все собственные числа оператора перехода В удовлетворяли условию:

(3.8)

Условие (3.8) - необходимое условие устойчивости разностных схем.

5.3. Устойчивость явной разностной схемы, аппроксимирующей дифференциальное уравнение параболического типа (3.3)

Наличие свободного члена в правой части дифференциального уравнения не оказывает влияния на устойчивость разностной схемы, аппроксимирующей это уравнение. Тогда отбрасываем свободный член ( ) и представляем решение разностной схемы (3.4) в виде гармоники (3.7):

Подставляя данное выражение в разностную схему, получаем:

Далее, упрощаем полученное выражение, деля левую и правую его части на :

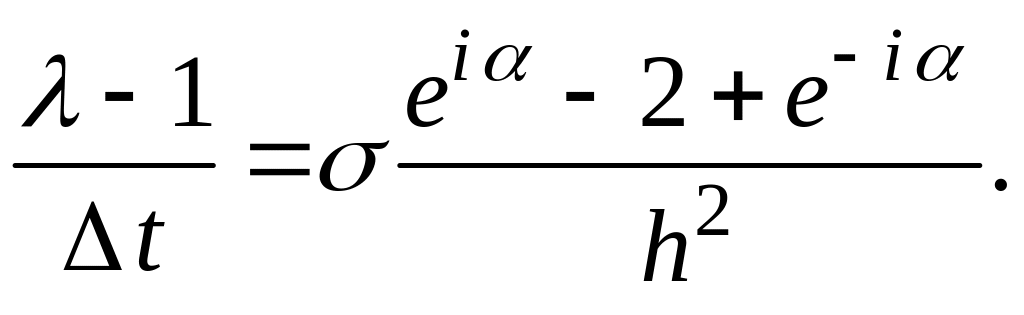
Преобразуем комплексные числа из экспоненциальной формы в тригонометрическую:

(3.9)

Используя тригонометрические тождества

(3.10)

получаем формулу, из которой затем выражаем :

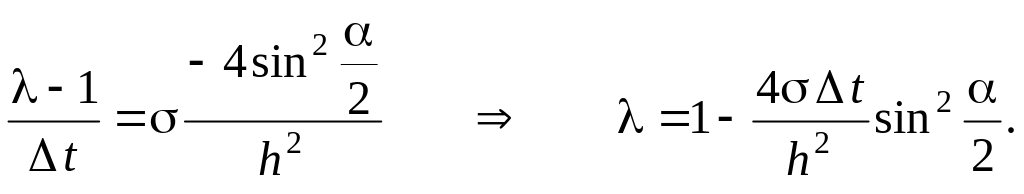
С учётом необходимого условия устойчивости разностных схем (3.8) имеем:

В полученном двойном неравенстве правое условие выполняется автоматически (если  > 0). Левое условие преобразуется:

(3.11)

Переходя к более строгому условию (заменяя на 1), получим условие устойчивости

(3.12)

явной разностной схемы, аппроксимирующей дифференциальное уравнение параболического типа, свободный член которого не включает искомую функцию u.

Условие (3.12) накладывает ограничение на выбор величины временного шага в зависимости от пространственного шага h. Такие разностные схемы называют условно устойчивыми.

5.4. Устойчивость неявной разностной схемы, аппроксимирующей дифференциальное уравнение параболического типа (3.3)

Неявная разностная схема, аппроксимирующая дифференциальное уравнение (3.3):

Как и для явной разностной схемы отбрасываем свободный член и представляем решение в виде гармоники

Далее, упрощаем полученное выражение, деля левую и правую его части на :

Используя зависимости (3.9), (3.10), получаем формулу, из которой затем выражаем :

Т.е. необходимое условие устойчивости неявной разностной схемы (3.8) в данном случае выполняется при любых значениях t и h. Такие разностные схемы, устойчивость которых не зависит от выбора интервала деления на разностной сетке, называют абсолютно устойчивыми.