
- •5.03050901 “Бухгалтерський облік“
- •5.03050401 “Економіка підприємства“
- •Загальні методичні рекомендації
- •Тема1. Елементи лінійної алгебри. Практичне заняття 1.1.
- •Практичне заняття 1.2.
- •Практичне заняття 1.3.
- •Тема: Аналітична геометрія . Векторна алгебра. Практичне заняття 2.1.1
- •Практичне завдання 2.1.2
- •Практичне заняття 2.2.
- •Тема3. Вступ до математичного аналізу. Практичне заняття 3.1.
- •Практичне заняття 3.2.1
- •Практичне заняття 3.2.2
- •Тема4. Диференціальне числення функції однієї змінної. Практичне заняття 4.1
- •Практичне заняття 4.2.
- •Практичне заняття 4.3
- •Практичне заняття 4.4.
- •Тема 5. Диференціальне числення функції багатьох змінних. Практичне заняття 5.1.1
- •Практичне заняття 5.1.2.
- •Тема 6. Інтегральне числення та диференціальні рівняння. Практичне заняття 6.1.
- •Практичне заняття 6.2.
- •Практичне заняття 6.3.1
- •Практичне заняття 6.3.2
- •Практичне заняття 6.4.
- •Екзаменаційні питання з вищої математики
- •Практичні завдання
- •Формула Ньютона-Лейбніца
- •Правила диференціювання
- •Перелік навчально-методичної літератури
Міністерство освіти і науки України
Сосницький сільськогосподарський технікум бухгалтерського обліку
ЗБІРНИК ПРАКТИЧНИХ ЗАВДАНЬ З ВИЩОЇ МАТЕМАТИКИ
За редакцією В. М. Пуда
Сосниця 2017
Міністерство освіти і науки України
Сосницький сільськогосподарський технікум бухгалтерського обліку
Збірник практичних завдань з вищої математики
За редакцією В. М. Пуда
Сосниця 2016
Укладач:
В. М. Пуд – викладач математики ССТБО
Рецензенти:
О. М. Ляшок – викладач фізики та математики ССТБО
ЗАВДАННЯ
Для самостійної роботи з курсу «Вища математика» для студентів ІІ курсу:
5.03050901 “Бухгалтерський облік“
5.03050401 “Економіка підприємства“
Розглянуто та затверджено на засіданні ц/к природознавчих та фізико-математичних дисциплін
Протокол № від 2017 року
Голова ц/к Логвін Н.П.
Загальні методичні рекомендації
Успішна реалізація досягнень науково-технічного прогресу та вирішення завдань, які ставить ринкова економіка, тісно пов’язані з використанням математичних методів та моделей при вирішенні багатьох проблем із різноманітних областей людської діяльності. Особливо важливого значення набуває використання математичних методів і засобів обчислювальної техніки в умовах ринкової економіки при розв’язанні економічних задач. У зв’язку з цим для студентів необхідні як знання можливостей застосування математичних методів та моделей у практичній діяльності, так і розуміння необхідності їх використання.
Завдання для практичних занять розроблено відповідно до програми рекомендованої Міністерством освіти і науки України для студентів економічних спеціальностей навчальних закладів I - II рівнів акредитації і включають практичні завдання по таких темах: « Елементи лінійної алгебри», « Аналітична геометрія. Векторна алгебра»,» Вступ до математичного аналізу», « Диференціальне числення функції однієї змінної», «Диференціальне числення функції багатьох змінних», «Інтегральне числення та диференціальні рівняння».
Після вирішення завдань, зазначених у даному посібнику, у повному обсязі студенти зможуть:
розв’язувати системи лінійних алгебраїчних рівнянь методом Крамера, Гаусса та матричним способом.
Обчислювати визначники n – порядку;
знаходити кут між векторами, довжину вектора, скалярний добуток векорів
знаходити кут між прямими; розрізняти рівняння та будувати пряму, коло, еліпс. Параболу, гіперболу за їх рівняннями;
знаходити границі послідовностей і функцій. Похідні функцій;
проводити дослідження функцій та будувати їх графіки;
знаходити частинні похідні та градієнти функцій багатьох змінних
знаходити екстремуми функцій багатьох змінних;
знаходити невизначений та обчислювати визначений інтгели;
обчислювати площі криволінійних трапецій а криволінійних фігур;
Тема1. Елементи лінійної алгебри. Практичне заняття 1.1.
Тема: Матриці, дії з ними.
Мета: Засвоїти поняття: матриця, елементи матриці, розмір матриці, протилежні матриці, транспоновані матриці. Ознайомитись з різновидами матриць, із сферами їх застосування. Набути навичок виконувати найпростіші дії з матрицями: множення на число, додавання та віднімання, множення матриць
Завдання 1.Знайти добуток матриць АВ або ВА.
а) А= (4
3 -2), В=
 .
.
б) А= ,
В= (4 -4 -1).
,
В= (4 -4 -1).
 в)
А=
в)
А=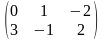 ,
В=
,
В= .
.
г) А= ,
В=
,
В= .
.
д) А=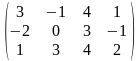 ,
В=
,
В=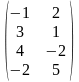 .
.
Завдання 2. Задамо матриці.
А= ;
В=
;
В= ;
С=
;
С= .
D=
.
D=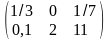 ;
P=
;
P=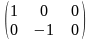
Виконати дії. а) А*В-С*ДТ; б) А*РТ+5А-Д
Завдання 3. За допомогою елементарних перетворень матриці знайти ранги матриць:
А=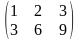 ;
В=
;
В= ;
С=
;
С= ;
Д=
;
Д= .
.
Завдання 4. Знайти обернені матриці за заданими двома способами:
а) за допомогою формули алгебраїчних доповнень;
б) за допомогою елементарних перетворень матриць:
А=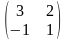 ;
В=
;
В=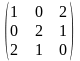 ;
С=
;
С= ;
Д=
;
Д= Е=
Е= F=
F= .
.
