Погрешности измерений

Независимо от тщательности измерения и совершенства измерительной техники абсолютно точно определить истинное значение измеряемой величины нельзя.

Погрешность измерения - есть отклонение результатов измерения от истинного значения измеряемой величины.

Различают: абсолютную, относительную и приведенную погрешности.

1. Абсолютная погрешность (А)- это разность между показанием прибора и действительным значением измеряемой величины.

А = A_п - А_д

где: А_п - показание измерительного прибора;

А_д - действительное значение измеряемой величины.

Абсолютная погрешность выражается в единицах измеряемой величины, она может быть положительной или отрицательной.

2. Относительная погрешность () - есть отношение абсолютной погрешности к действительному значению измеряемой величины, выражается в процентах.

,

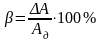3. Приведенная погрешность (_пр) - это отношение абсолютной погрешности к полному пределу измерения по шкале прибора.

,

где А - абсолютная погрешность;

Х - полный предел измерения.

Класс точности прибора - это величина его приведенной погрешности.

Только _пр выражается в процентах, а класс точности - есть величина безразмерная.

Пример:

Определить абсолютную, относительную и приведенную погрешности прибора с верхним пределом измерения 150⁰С при показании его Ап = 120⁰С и действительном значении измеряемой температуры Ад = 120,6⁰С.

Х = 1500С Aп = 1200C Aд = 120,60С		A = Aп - Aд = 1200C - 120,60C = - 0,60C
A = ? β = ? γпр =?

Определение допустимой заводской погрешности прибора

Так как классифицировать приборы по абсолютной погрешности весьма неудобно (эти погрешности могут иметь разное значение у каждого отдельного экземпляра из серии одинаковых по конструкции, но разных по качеству изготовления приборов), то для оценки точности прибора вводится понятие допустимой заводской погрешности.

Ее определяют по формуле:

,

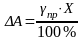где _пр - относительная приведенная погрешность (численно равна классу точности, но выражается в %);

Х - полный предел шкалы;

A – допустимая заводская погрешность.

Допустимая погрешность - это наибольшая погрешность показания прибора, допустимая нормами. При величине допустимой погрешности указывают ее знаки  или один из них.

Пример:

Манометр имеет предел измерения от 0 до 6 кгс/см². Класс точности прибора равен 2,5.

Определить допустимую заводскую погрешность.

Х = 6 кгс/см² _пр  Х

_пр = 2,5 % А =

100 %

А = ? 2,5  6

А = =  0,15 кгс/см²

100

Точность измерения зависит от класса точности и от предела измерения прибора.

Чем класс точности выше и, чем меньше предел измерения, тем прибор точнее.

Пример:

Имеются два манометра с классом точности 1. Один имеет предел измерения от 0 до 1 кгс/см², второй - от 0 до 4 кгс/см².

Определить, какой прибор точнее.

_пр  Х

Х₁ = 1 кгс/см²  А =

Х₂ = 4 кгс/см² 100%

_пр1 = _пр2 = 1 % _пр1  Х ₁ 1  1

А₁ = = = 0,01 кгс/см²

А₁ =? 100% 100

А₂ =? _пр2  Х ₂ 1  4

А ₂ = = = 0,04 кгс/см²

100% 100

Первый прибор точнее, т.к. его допустимая погрешность меньше.