3. Методические указания к контрольной работе

При решении задач «Технической механики» студент должен уметь применять совокупность знаний, полученных при изучении различных разделов и тем дисциплины.

К задаче 1. К решению задачи следует приступать после изучения тем «Условия равновесия сходящейся плоской системы сил», «Связи и их реакции», «Условие прочности при растяжении-сжатии», «Расчеты по предельным нагрузкам».

Пример 1. Дано: Р = 10 кН; АС= 4 м. Определить реакции в стержнях АС и ВС (рис. 1,а). Подобрать сечение стержней: для стержня ВС в виде трубы с соотношение диаметров d/D=0,8, для стержня АС – квадратное сечение, если расчетное сопротивление растяжению материала R_р=76 МПа, расчетное сопротивление материала сжа­тию R_cж=102 МПа; коэффициент условий работы γ_с =1,2; 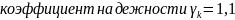. Определить удлинение (укорочение) стержней.

Рис.1,а Рис.1,б

Решение:

1.Выбираем точку равновесия – точку С, в которой сходятся все силы.

2.Освобождаем тело от связей, заменяя их действие реакциями. В данном случае реакциями N_ВС и N_AC , направленными вдоль стержней (рис. 1,б). При этом предполагаем, что оба стержня растянуты, то есть усилия направляем от точки С.

3.Выбираем оси координат х и y, принимая ось х перпендикулярно стержню АС.

4. Для полученной плоской сходящейся системы сил составляем уравнения равновесия.

Pcos45 – N_ВСsin30 = 0; (1)

Pcos45 + N_AC+ N_DCcos30 = 0; (2)

Из уравнения (1): кH.

Значение усилия получилось положительным, следовательно, стержень ВС работает на растяжение.

Из уравнения (2):

.

Усилие получилось отрицательным, следовательно, стержень АС работает на сжатие.

Для проверки построим силовой многоугольник (рис. 2).

5. Подбор сечения осуществляем, используя условие прочности при растяжении-сжатии:

,

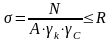
г

Рис. 2. Силовой многоугольник

де — расчетное усилие, возникшее в элементах конструкции от расчетных внешних нагрузок; А — площадь сечения элемента; R — расчетное сопротивление материала растяжению (сжа­тию); γ_с — коэффициент условий работы; 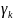- коэффициент на­дежности.

Д

Рис. 2

ля стержня ВС: мм².

Так как площадь трубы ,

то .

Для стержня АС: мм².

Так как площадь квадрата , то .

6. Определяем длину стержня ВС:

1. Удлинение каждого стержня определим по формуле:

где l – длина стержня, м,

N – усилие в стрежне, кН,

А – площадь поперечного сечения в стержне, м²,

Е – модуль упругости, Па.

К задаче 2. К решению задачи следует приступать после изучения тем «Условия равновесия произвольно расположенной пространственной системы сил», «Виды балочных опор», «Расчет составных элементов конструкций», «Условие прочности при изгибе».

Пример 2. Для балки, представленной на рис. 3, а определить реакции опор и давления в промежуточных шарниров; построить эпюры поперечных сил и изгибающих моментов; подобрать сечение для каждого пролета балки из двутавра, если допустимое напряжение [σ]=160 МПа.

Решение: Составная балка представляет собой систему простых балок, соединенных шарнирами. Поэтому при решении задачи можно рассмотреть системы уравновешивающихся сил, приложенных к каждой простой балке в отдельности, учитывая давление в шарнирах, соединяющих эти балки.

Так как шарнир эквивалентен шарнирно-неподвижной опоре по числу связей и степеней свободы, то, заменив шарниры в балке на шарнирно-неподвижные опоры, можно построить поэтажную схему.

2. Определяем опорные реакции, изгибающие моменты и поперечные силы в характерных сечениях полученных простых двухопорных балок.

1) Для балки FL (рис. 4,б) определяем опорные реакции R_F и R_K из уравнений равновесия:

∑ M_K = 0: –R_F l₁ + m + 2P₂ = 0, откуда R_F = 4,7 кН,

∑ M_F = 0: –R_Kl₁ + m + P₂(l₁ + 2) = 0, откуда R_K = 13,7 кН.

Проверяем правильность определения реакций:

∑ Fy = 0: –R_F + R_K – P₂ = 0.

Реакции балки вычислены правильно.

Изгибающий момент и поперечная сила в сечении x₁ при изменении x₁ от 0 до 8м вычисляются по формулам:

M_x1 = –R_F x₁ + m + R_K(x₁ – l₁);

Q_x1 = –R_F + R_K;

При x₁ = 0 м: M_x1 = 0 кН · м, Q_x1 = –R_F = –4,7 кН,

x^лев₁ = 3 м: M^лев_x1 = –14 кН · м, Q^лев_x1 = –R_F = –4,7 кН,

x^прав₁ = 3 м: M^прав_x1 = –4 кН · м, Q^прав_x1 = –R_F = –4,7 кН,

x^лев₁ = 6 м: M^лев_x1 = –18 кН · м, Q^лев_x1 = –R_F = –4,7 кН,

x^прав₁ = 6 м: M^прав_x1= –18 кН · м, Q^прав_x1= –R_F + R_K = 9 кН,

x₁ = 8 м: M_x1 = 0 кН · м, Q_x1 = –R_F + R_K = 9 кН.

Рис. 3

Рис. 4

2) Проведем аналогичные расчеты для балки АС (см. рис. 4,а)

∑ M_C = 0: R_B l₂ – P₁(l₂ – 2) – q₁(l₂ +2)²/2= 0, R_B = 41 кН.

∑ M_B = 0: –R_C l₂ +P₁(l₂ - 2) – q₁ ·2² / 2 + q₁ (l₂)² / 2 = 0, R_C = 17 кН.

Проверка реакций: ∑ y = 0: R_B +R_C –P₁ – q₁ ·6 = 0. Реакции вычислены правильно.

Изгибающий момент и поперечная сила в сечении х₂ при изменении х₂ от 0 до 6м вычисляются по формулам

M_x2 = R_B(x₂ – 2) – P₁(x₂ – 4) – q₁(x₂)² / 2;

Q_x2 = –q x₂ + R_B – P₁;

При x₂ = 0 м: M_x2 = 0 кН · м, Q_x2 = 0 кН,

x^лев₂ = 2 м: M^лев_x2 = –16 кН · м, Q^лев_x2 = 16 кН,

x^прав₂ = 2 м: M^прав_x2 = –16 кН · м, Q^прав_x2 = 25 кН,

x^лев₂ = 4 м: M^лев_x2 = 18 кН · м, Q^лев_x2 = 9 кН,

x^прав₂ = 4 м: M^прав_x2= 18 кН · м, Q^прав_x2 = –1 кН,

x₂ = 6 м: M_x2 = 0 кН · м, Q_x2 = –17 кН.

3) Расчет главной балки CF. Загружаем ее в точках C и F давлением вышележащих балок R_D и R_E (реакциями с обратными знаками) (см. рис. 4,в) и вычисляем опорные реакции.

∑ M_E = 0: R_D l – R_C ·8 – q₂ 8² / 2 + q₂ 2² / 2 – R_F · 2 = 0,

откуда R_D = 44,2 кН.

∑ M_D = 0: –R_E l + q₂ ·8² / 2 – q₂ ·2² / 2 – R_F ( l + 2) = 0,

откуда R_E = 8,07 кН.

Проверяем правильность определения реакций.

∑ y = 0: R_E +R_D+R_F –q₂ ·10 –R_C = 0.

Реакции вычислены правильно.

Изгибающие моменты и поперечные силы в сечении х при изменении х от 0 до 10 м вычисляются по формулам:

М_{х =} –R_C х – q₂ х² / 2+ R_D(x₂ – 2)+ R_Е(x – 8);

Q_х = –R_C – q₂ х+ R_D + R_Е.

При x = 0 м: M_x = 0 кН · м, Q_x = –R_D = –17 кН,

x^лев = 2 м: M^лев_x = –42 кН · м, Q^лев_x = –25 кН,

x^прав = 2 м: M^прав_x = –42 кН · м, Q^прав_x = 19,2 кН,

x^лев = 8 м: M^лев_x = 13 кН · м, Q^лев_x = –4,7 кН,

x^прав = 8 м: M^прав_x = 13 кН · м, Q^прав_x = 3,3 кН,

x = 10 м: M_x = 0 кН · м, Q_x = –4,7 кН.

По вычисленным значениям M и Q строятся эпюры внутренних усилий для каждой простой балки (см. рис. 4) и для многопролетной балки AL (см. рис. 3,в).

Подбираем сечение балки. Условие прочности при изгибе:

следовательно, требуемый момент поперечного сечения балки:

Для пролета АD, DE:

По таблице сортамента принимаем двутавр №24 с W_х=289 см³;

Для пролета ЕК:

По таблице сортамента принимаем двутавр №18 с W_х=143 см³;

К задаче 3. К решению задачи следует приступать после изучения тем «Построение кинематических схем», «Общие сведения о передачах».

П ример 3. Привод (рис. 6) состоит из электродвигателя мощностью Р_дв=1,9 кВт с частотой вращения n_дв=1440 мин-1, редуктора и цепной передачи. u_P=1,6. Определить:

- угловые скорости валов

-

2

передаточные числа

- общий К.П.Д.

- вращающие моменты на всех валах.

Решение:

1. Определяем передаточное число цепной передачи:

Тогда передаточное число всего привода:

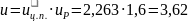
2. Определяем угловые скорости вращения валов:

-

Рис. 6

угловая скорость вращения ведущего вала цепной передачи (вала электродвигателя)

- угловая скорость вращения ведомого вала цепной передачи (ведущего вала редуктора)

-угловая скорость вращения ведомого вала редуктора

3. Определяем вращающий момент на валах:

на валу электродвигателя:

на ведущем валу редуктора:

,

то , где – КПД цепной передачи

на ведомом валу редуктора:

где

Здесь КПД закрытой зубчатой передачи с цилиндрическими колесами; пары подшипников качения;

тогда

4. Определяем общий КПД всего привода:

К задаче 4. К решению задачи следует приступать после изучения тем «Условия равновесия произвольно расположенной пространственной системы сил», «Гипотезы прочности и их применение».

Пример 4. Для вала постоянного поперечного сечения (рис. 8, а) требуется:

1. Построить эпюру крутящих моментов;

2. Построить эпюры изгибающих моментов в вертикальной и горизонтальной плоскостях;

3. Из условия прочности определить допускаемое значение передаваемой мощности, если угловая скорость вращения вала 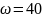рад/сек и допускаемое напряжение МПа.

Решение. На рис. 8,б показана расчетная схема вала, полученная после замены опор реакциями.

Рис. 8.

1. Составляем для полученной пространственной системы сил уравнения равновесия:

(1)

(2)

(3)

(4)

(5)

(6)

Из уравнения (6):

При этом:

Определяем реакции опор:

Из уравнения (4):

Из уравнения (5):

Из уравнения (1):

_{Из уравнения (2):}

2. Построим эпюр крутящих моментов (рис. 8 , д).

3. Определим изгибающие моменты в горизонтальной плоскости и построим их эпюру (рис. 8, в):

=0

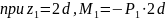
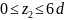
4. Определим изгибающие моменты в вертикальной плоскости и построим их эпюру (рис. 8, г):

=0

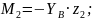
Опасным является сечение 1 (сечение над левой опорой вала) . Применяя третью гипотезу прочности, находим

Выразим окружное усилие через и

тогда

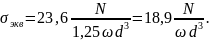
Из условия прочности находим

Вт =36 кВт.

К задаче 5. К решению задачи следует приступать после изучения тем «Применение законов статики к расчету стержневых систем», «Определение прогибов и углов поворота шарнирно-стержневых систем». При этом необходимо отметить, что способов определения углов поворота и прогибов балки существует несколько и можно воспользоваться любым.

П ример 5. Однопролетная балка находится под действием сосредоточенной силы Р (рис.9, а). Найти дифференциальное уравнение изгиба и найти максимальные прогибы и углы поворота.

Р

z₁

ешение. 1) Опор­ные реакции . Балка имеет два участка с различными выражениями для изгибающих моментов:

(1)

В

Рис. 9

этом случае дифференциальные уравнения изгиба на каждом из участков име­ют различный вид: (2)

Интегрирование этих уравнений приведет к выражениям для прогибов v₁, v₂, которые будут содержать четыре постоянные интегрирования. Для их определения нужно составить четыре граничных условия. Это вызовет определенные трудности при решении данной задачи. Метод начальных параметров существенно упрощает решение задачи по определению прогибов балки.

Составим выражения прогибов для каждого из участков, пользуясь формулой:

,

где z – расстояние от начала координат до сечения;

а, b, c – расстояние от начала координат до точек приложения сил, моментов, распределенной нагрузки;

v₀, θ₀ – прогиб и угол поворота вначале координат.

В нашем случае с учетом правила знаков эти уравнения примут вид:

(3)

(4)

Начальные параметры определяем из граничных условий:

(5)

Подставляя в (3) и в (4), согласно (5), находим:

(6)

откуда получаем:

(7)

П одставляя значения в (3), (4), получим выражения прогибов на каждом из двух участков. Максимальный прогиб находим из (3) либо (4) при . В результате вычислений находим:

(8)

Угол поворота на втором участке:

На правой опоре В при z =l получаем:

П

Рис. 10

ример 6. Определить перемещение точки К балки (рис. 10) при помощи интеграла Мора.

Решение:

1) Составляем уравнение изгибающего момента от внешней силы M_F.

2) Прикладываем в точке К единичную силу F = 1.

3) Записываем уравнение изгибающего момента от единичной силы 

4) Определяем перемещения:

 

Пример 7. Определить перемещение точки К (рис. 11) балки по способу Верещагина.

Решение:

1) Строим грузовую эпюру ЭМ_р.

2) Прикладываем в точке К единичную силу.

3) Строим единичную эпюру ЭМ₁.

4) Определяем прогиб

,

где ω – площадь эпюры ЭМ_р,

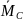– значение момента на эпюре ЭМ₁ под центром тяжести фигуры (треугольника) с эпюры моментов ЭМ_р.

Рис. 11

;      ;    

Пример 6. Для балки определить прогиб и угол поворота сечения в точке приложения силы методом начальных параметров и интегралом Мора способом Верещагина.

Решение:

Определим прогиб и угол поворота сечения в точке приложения силы интегралом Мора способом Верещагина.

1) Для этого строим эпюру изгибающих моментов от заданной нагрузки. Разбиваем эту эпюру в интервале от жесткой заделки до точки приложения нагрузки на простые фигуры (рис. 11,а).

2) Находим площадь эпюры А′ и статический момент S′ каждой фигуры.

, где приложена сила Р.

Рис. 11, а. К определению прогиба и угла поворота сечения