- •Значение величин и при несовершенном сжатии
- •Значения коэффициентов расхода для больших отверстий
- •Коэффициенты e, j, m и X для различных типов насадков
- •Р авномерным движением в открытом русле будет такое установившееся движение, при котором в соответственных точках любых двух сечений скорости одинаковы по величине и по направлению
- •Гравитационные волны на мелкой воде
- •Гравитационные волны на глубокой воде
1
Жидкость - физическое тело, которое обладает свойством текучести, т. е. не имеющее способности самостоятельно сохранять свою форму.Текучесть жидкости обусловлена подвижностью молекул, составляющих жидкость.
Жидкостью называется агрегатное состояние вещества, промежуточное между твердым и газообразным. Жидкость характеризуется следующими свойствами: 1) сохраняет объем; 2) образует поверхность; 3) обладает прочностью на разрыв; 4) принимает форму сосуда; 5) обладает текучестью. Свойства жидкости с 1) по 3) подобны свойствам твёрдых тел, а свойство 4) - свойству газа.
Жидкости, законы движения и равновесия которых изучаются в гидравлике (механике жидкости и газа), делятся на два класса: сжимаемые жидкости или газы, почти несжимаемые - капельные жидкости. В гидравлике рассматриваются как идеальные, так и реальные жидкости.
Идеальная жидкость - жидкость, между частицами которой отсутствуют силы внутреннего трения. Вследствие этого такая жидкость не сопротивляется касательным силам сдвига и силам растяжения. Идеальная жидкость совершенно не сжимается, она оказывает бесконечно большое сопротивление силам сжатия. Такой жидкости в природе не существует - это научная абстракция, необходимая для упрощения анализа общих законов механики применительно к жидким телам.
Реальная жидкость - жидкость, которая не обладает в совершенстве свойствами идеальной жидкости, она в некоторой степени сопротивляется касательным и растягивающим усилиям, а также отчасти сжимается. Для решения многих задач гидравлики этим отличием в свойствах идеальной и реальной жидкостей можно пренебречь. В связи с этим физические законы, выведенные для идеальной жидкости, могут быть применены к жидкостям реальным с соответствующими поправками.
2
В покоящейся жидкости возникают только напряжения сжатия и не могут действовать касательные напряжения, так как любое касательное напряжение жидкости вызовет ее движение, т.е. нарушит состояние покоя. В главе 1 было показано, что напряжения сжатия вызывает сила, действующая перпендикулярно на бесконечно малую площадку. Отсюда вытекает первое свойство гидростатического давления: гидростатическое давление действует по нормали к поверхности и является сжимающим, то есть действует внутрь рассматриваемого объема.
Второе свойство гидростатического давления состоит в том, что в любой точке внутри покоящейся жидкости гидростатическое давление не зависит от ориентировки площадки, по которой оно действует, то есть одинаково во всех направлениях.

Гидравлический пресс – это машина для обработки материалов давлением, приводимая в действие сдавливаемой жидкостью. В основе ее работы лежит закон Паскаля, который, кстати, и изобрел гидравлический пресс, только называл он его «машиной для увеличения сил».
Состоит гидравлический пресс из двух соединенных между собой сосудов различного сечения, наполненных минеральным маслом или водой. Так как давление в жидкостях передается одинаково во все стороны, то приложив некоторое давление на жидкость в малом сосуде, мы получим такое же давление в большом сосуде на единицу площади.
Но, так как сечение большого сосуда будет значительно больше, то и давление, оказываемое по всей площади сечения, будет больше во столько раз, во сколько раз больше площадь этого сечения.
А, поместив между столбом жидкости в большем сосуде и неподвижной опорой некоторое тело, мы и получим давление на тело, превосходящее приложенное в несколько раз.
Например, если разница в сечениях сосуда у нас стократна, то и сила, получаемая на выходе, будет больше приложенной в сто раз. Вот таким образом и можно увеличить силу своих рук во много раз, не применяя дополнительные источники сил.
Гидравлический мультипликатор — устройство для повышения давления жидкости, состоящее из двух соединённых между собой цилиндров. В цилиндре низкого давления находится поршень большого диаметра D, который соединён с плунжером малого диаметра d, входящим в цилиндр высокого давления. Получаемое давление pв будет в D2/d2 раз больше подводимого pн (в численном выражении в 40—60 раз).
Мультипликаторы - это гидравлические устройства, позволяющие изменять соотношение давлений рабочей среды входного (управляющее давление) и выходного (увеличенное давление) звеньев, при постоянной мощности (если пренебречь трением в уплотняемых парах, например: плунжер-корпус).
3
Судно, яхта подвержены действию сил и моментов сил, стремящихся наклонить их в поперечном и продольном направлениях. Способность судна противостоять действию этих сил и возвращаться в прямое положение после прекращения их действия называется остойчивостью
Метацентр - центр кривизны траектории. Различают два метацентра:
при наклонении судна в поперечной плоскости (крен), метацентр является поперечным, или малым.
при наклонении судна в продольной плоскости (дифферент) — продольным, или большим.
Метацентрическая высота — критерий остойчивости судна. Представляет собой возвышение метацентра над центром тяжести плавающего тела.
Радиус кривизны траектории, по которой перемещается центр величины при поперечных наклонениях называется поперечным метацентрическим радиусом r. Другими словами — это расстояние между поперечным метацентром и центром величины
4
Используют манометры, вакуумметры, мановакуумметры, напоромеры, тягомеры, тягонапоромеры, датчики давления, дифманометры. В большинстве приборов измеряемое давление преобразуется в деформацию упругих элементов, поэтому они называются деформационными.
Деформационные приборы широко применяют для измерения давления при ведении технологических процессов благодаря простоте устройства, удобству и безопасности в работе. Все деформационные приборы имеют в схеме какой-либо упругий элемент, который деформируется под действием измеряемого давления: трубчатую пружину, мембрану или сильфон
Манометров и вакуумметров c максимальным пределом измерений. В таких приборах с изменением измеряемого давления р трубчатая пружина / изменяет свою кривизну. Её свободный конец через тягу поворачивает зубчатый сектор и находящуюся с ним в зацеплении шестерню. Вместе с шестерней поворачивается закрепленная на ней стрелка, перемещающаяся вдоль шкалы. Деформация мембраны, пропорциональная приложенному давлению, приводит к деформации тензорезистора и изменению его сопротивления
Единицей измерения давления в ней является Паскаль, Па(Ра)-1Па=1Н/кв.м.Производные от этой единицы 1 кПа=1000 Па и 1МПа=1000000 Па. В различных отраслях техники используются следующие единицы: миллиметр ртутного столба (мм.рт.ст или Торр), физическая атмосфера (атм.), техническая атмосфера (1 ат. = 1 кгс/кв.см), бар. В англоязычных странах популярностью пользуется фунт на квадратный дюйм (pounds per square inch или PSI).
АТМОСФЕРНОЕ давление, давление атмосферы воздуха нанаходящиеся в нем предметы и на земную поверхность. В каждой точке атмосферы атмосферное давлениеравно весу вышележащего столба воздуха; с высотой убывает. Среднее атмосферное давление на уровнеморя эквивалентно давлению 760 мм рт. ст. Вакуумметрическое давление, или вакуум, — недостаток давления до атмосферного (дефицит давления), т. е. разность между атмосферным или барометрическим и абсолютным давлением:
5
В покоящейся жидкости всегда присутствует сила давления, которая называется гидростатическим давлением. Жидкость оказывает силовое воздействие на дно и стенки сосуда. Частицы жидкости, расположенные в верхних слоях водоема, испытывают меньшие силы сжатия, чем частицы жидкости, находящиеся у дна.
Свойство 1. В любой точке жидкости гидростатическое давление перпендикулярно площадке касательной к выделенному объему и действует внутрь рассматриваемого объема жидкости.
Свойство 2. Гидростатическое давление неизменно во всех направлениях.
Свойство 3. Гидростатическое давление в точке зависит от ее координат в пространстве. по мере увеличения погружения точки давление в ней будет возрастать, а по мере уменьшения погружения уменьшаться


6
Пусть имеется фигура произвольной формы площадью со в плоскости Оl, наклоненной к горизонту под углом α (рис. 3.17).
Для удобства вывода формулы для силы
давления жидкости на рассматриваемую
фигуру повернем плоскость стенки на
90° вокруг оси 01 и
совместим ее с плоскостью чертежа.
Выделим на рассматриваемой плоской
фигуре на глубине h от
свободной поверхности жидкости
элементарную площадку dω.
Тогда элементарная сила, действующая
на площадку dω, будетР ис.
3.17. Схема к определению силы давления
жидкости на плоскую стенку
ис.
3.17. Схема к определению силы давления
жидкости на плоскую стенку
Интегрируя
последнее соотношение, получаем суммарную
силу давления жидкости на плоскую
фигуру![]() Учитывая,
что
Учитывая,
что ![]() ,
получаем
,
получаем![]()
или![]() Последний
интеграл равен статическому моменту
площадки со относительно
оси Оу, т.е.
Последний
интеграл равен статическому моменту
площадки со относительно
оси Оу, т.е.![]() где lС – расстояние
от оси Оу до центра тяжести фигуры.
Тогда
где lС – расстояние
от оси Оу до центра тяжести фигуры.
Тогда
![]() Так
как
Так
как ![]() ,
то
,
то![]()
т.е. суммарная сила давления на плоскую фигуру равна произведению площади фигуры на гидростатическое давление в ее центре тяжести.
Точка приложения суммарной силы давления (точка d, см. рис. 3.17) называется центром давления. Центр давления находится ниже центра тяжести плоской фигуры на величину е. Последовательность определения координат центра давления и величины эксцентриситета изложена в параграфе 3.13.
В частном
случае вертикальной прямоугольной
стенки получим (рис. 3.18)

7

Тело давления ограничивается криволинейной поверхностью, вертикальными поверхностями, проходящими через крайние точки криволинейной поверхности, и свободной поверхностью жидкости или ее продолжением. Вертикальная составляющая направлена вниз, если тело давления заполнено жидкостью(реальное тело давления). Вертикальная составляющая направлена вверх, если тело давления не заполнено жидкостью (фиктивное, воображаемое тело давления).
На
рис.3 оказаны некоторые характерные
случаи построения тел давления.
Знаком ![]() отмечены
реальные тела давления, а знаком
отмечены
реальные тела давления, а знаком ![]() -фиктивные.
-фиктивные.
Построение тел давления для криволинейных поверхностей, имеющих сложную конфигурацию, целесообразно выполнять по частям.
Криволинейную поверхность плоскостями разбивают на простейшие фигуры, для которых строят тела давлений. Результирующее тело давления получают суммированием простейших тел давления с учетом направления вертикальной составляющей силы гидростатического давления.
В случае,если однородная жидкость находится с двух сторон криволинейной поверхности (стенки), тело давления строят аналогичным образом
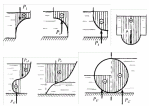
Рис.3Тела давлений и направление вертикальной составляющей силы гидростатического давления жидкости.
Результирующая
сила гидростатического давления жидкости
на криволинейную поверхность определяется
по формуле![]()
8

Центром тяжести механической системы называется точка, относительно которой суммарный момент сил тяжести (действующих на систему) равен нулю Центр величины — это воображаемая точка приложения равнодействующей сил плавучести.Известен также как центр водоизмещения тела. Плавучестью судна называется его способность держаться на воде по определенную осадку, неся предназначенные грузы в соответствии с назначением судна. Остойчивостью называется способность судна противостоять, силам, вызвавшим его наклонение, и после прекращения действия этих сил возвращаться в первоначальное положение. Наклонения судна возможны по разным причинам: от действия набегающих волн, из-за несимметричного затопления отсеков при пробоине, от перемещения грузов, давления ветра, из-за приема или расходования грузов и пр. Наклонение судна в поперечной плоскости называют креном , а в продольной плоскости — дифферентом ; углы, образующиеся при этом, обозначают соответственно O и y,
9
Движение жидкости, как и всякого тела, может быть равномерным и неравномерным по пути движения. Кроме того, движение жидкости может быть постоянным и переменным по времени (устойчивым или неустойчивым). Рассмотрим отдельно эти виды движений: a) Равномерным движением называется такое движение, при котором скорости в подобных точках двух смежных сечений равны между собой, а траектории частиц прямолинейны и параллельны. Говорят, что поле скоростей не меняется течения. Ускорения частиц жидкости при этом равен нулю. В этом случае параметры потока не меняются течения. b) Неравномерное движение - такое движение, при котором параметры потока (например, скорости частиц жидкости) меняются течения. c) Устойчивое движение - такое движение, при котором в любой точке пространства скорость течения не меняется ни по направлению, ни по величине по времени. Очевидно, что постоянное движение может быть и равномерным и неравномерным. d) Неустановившиеся движение - движение, меняется по времени. e) Сплошное и прерывистое движения. Если движение происходит без образования пустот внутри движущейся жидкости, то он называется сплошным, в противном случае - прерывистым. Течение воды в реках - сплошное движение, а на - прерывистое.
Поток жидкости характеризуется такими параметрами как площадь живого сечения S, расход жидкости Q(G), средняя скорость движения v. Живое сечение потока — это сечение, которое перпендикулярно в каждой точке скорости частиц потока жидкости. Расход жидкости — это количество жидкости, протекающей через живое сечение потока в единицу времени. Расход может определяться в массовых долях G и объемных Q. Средняя скорость движения жидкости — это средняя скорость частиц в живом сечении потока. Ламинарное движение — это упорядоченное движение жидкости без перемешивания между ее соседними слоями. При ламинарном течении скорость и силы инерции, как правило, невелики, а силы трения значительны. При увеличении скорости до некоторого порогового значения ламинарный режим течения переходит в турбулентный. Турбулентное движение — это течение жидкости, при котором ее частицы совершают неустановившееся беспорядочное движение по сложным траекториям. При турбулентном течении скорость жидкости и ее давление в каждой точке потока хаотически изменяется, при этом происходит интенсивное перемешивание движущейся жидкости.
10
Существует два метода изучения движения жидкости: метод Эйлера и метод Лагранжа.
1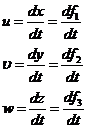 .
Метод Лагранжа: выделяется частица в
движущейся жидкости и исследуется ее
траектория в зависимости от координат
и времени.
.
Метод Лагранжа: выделяется частица в
движущейся жидкости и исследуется ее
траектория в зависимости от координат
и времени.
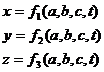
a,
b, c –
это постоянные, которые определяют
положение точки в начальный момент
времени.
![]()
2. Метод Эйлера: задается метод распределения скорости в потоке в зависимости от координат и времени:
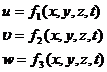 x,
y, z –переменные
Эйлера.
x,
y, z –переменные
Эйлера.
Чтобы определить скорости в какой-либо точке надо задать ее координаты. Поле ускорений потока можно получить если продифференцировать систему (3):
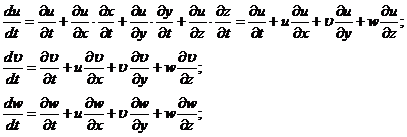
Получили систему, описывающую поле ускорений.
Локальные
ускорения, показывающие как изменяется
скорость в какой-либо точке потока с
течением времени![]()
Конвективные
ускорения (все остальное в правой части),
связанные с перемещением точки или
среды (т.е. с конвекцией). Течение может
быть стационарным или нестационарным
(изменяется во времени). Для стационарных
задач локальные ускорения равны нулю.
Самые простые течения стационарные,
плоские и одномерные. Для стационарной
и плоской задачи исследуется течение
только по двум координатам. Если
рассматривается
одномерная стационарная задача, тогда![]()
11
Уравнение Бернулли для потока имеет вид:
![]() .
.
Уравнение Бернулли имеет геометрический и энергетический смысл.
Геометрический смысл:
в геометрическом смысле каждый из членов уравнения выражает высоту (напор), что легко доказать проанализировав размерность каждого члена,
• z - геометрический напор ="м
• p/ρg - пьезометрический напор = (Н/м2) / (Н/м3) = м
• z +p/ρg - гидростатический напор
• V2/2g - скоростной напор = (м2/с2)/ (м/с2) = м
• hn - потери напора = м
Сумма всех составляющих - полный напор. C геометрической точки зрения уравнение Д. Бернулли можно прочитать так: напорная линия по длине потока всегда понижается, так как часть напора тратится на преодоление трения по длине поток.
Энергетический смысл:
в энергетическом смысле каждый из членов уравнения выражает величину удельной энергии потока, т.е. энергию, приходящуюся на единицу массы движущейся жидкости,
Сумма всех составляющих - полная удельная энергия. Следовательно, энергетический смысл можно выразить так: при установившемся движении потока реальной жидкости сумма четырех удельных энергий остается неизменной вдоль потока
12
В отличие от идеальной жидкости при движении реальной жидкости часть энергии , которой она располагает,, расходуется на преодоление гидравлических сопротивлений. Поэтому начальная общая энергия жидкости не остается постоянной по длине струйки или потока, а уменьшается от сечения к сечению. При этом происходит необратимое преобразование гидромеханической энергии в тепловую. Тогда уравнение Бернулли для реальной жидкости должно учитывать энергию, затраченную на преодоление гидравлических сопротивлений hn. Эту составляющую вносят в правую часть уравнения. Уравнение запишется в виде:
![]() .
.
Для характеристики относительного изменения полного напора по длине потока вводят понятие гидравлического уклона.
Средний гидравлический уклон на участке между сечениями 1–1 и 2–2 (рис. 4.6) определяется как отношение потери напора к длине участка:
 ,
,
где l1-2 - расстояние (по пути движения) между сечениями 1–1 и 2–2.
Гидравлический уклон - безразмерная положительная величина.
Гидравлический уклон в сечении потока определяется выражением
![]() .
.
Знак «-» указывает на убывание полного напора по течению.
 Понятие
об уклоне можно ввести и для пьезометрической
линии.
Понятие
об уклоне можно ввести и для пьезометрической
линии.
Средний пьезометрический уклон
![]() .
.
Пьезометрический уклон для некоторого сечения потока
![]() .
.
Пьезометрический уклон может быть положительным, равным нулю и отрицательным.
13
Конструктивно водомер Вентури состоит из конфузора (конически сходящийся участок) и диффузора (конически расходящийся участок), соединенных между собой цилиндрическим калиброванным участком трубы с диаметром d, меньшим, чем диаметр трубопровода D (Рис. 3.6).
Малая длина водомера (расстояние между сечениями I и II) и плавные переходы между его элементами позволяют пренебречь потерями напора в приборе. Для водомера, имеющего фиксированные значения D и d, с – величина постоянная, которая называется постоянной водомера Вентури.
.
Расход определяется выражением:
 где
где
Q — объемный расход жидкости
C — экспериментальный коэффициент, отражающий потери внутри расходомера,
A1 и A2— площади сечения трубопровода и горловины соответственно,
ρ — плотность жидкости или газа,
P1 и P2 — статические давления на входе трубы и в горловине.
В случае измерения расхода газа в выражение вводят коэффициент сжимаемости газа. В основе принципа действия трубки Вентури лежит эффект Вентури — явление уменьшения давления в потоке жидкости или газа, когда этот поток проходит через суженный участок трубы, что, в свою очередь, является прямым следствием действия закона Бернулли.
14
Полученное уравнение Бернулли справедливо и для газа, при условии, что скорость его движения значительно меньше скорости звука.
Таким образом, полный напор в потоке реальной жидкости не остается постоянным, а все время уменьшается вдоль потока, причем в общем случае, неравномерно
Для элементарной струйки:

Для потока реальной жидкости

15
В зависимости от рода жидкости, скорости ее движения и характера стенок, ограничивающих поток, различают два основных режима движения: ламинарный и турбулентный. Ламинарным называют упорядоченное движение, когда отдельные слои скользят друг по другу, не перемешиваясь (рис. 26, а).
Ламинарный режим движения можно наблюдать чаще у вязких жидкостей, таких как нефть, масла и т. п.
 Турбулентным называют
режим, при котором наблюдается
беспорядочное движение, когда частицы
жидкости движутся по сложным траекториям
и слои жидкости постоянно перемешиваются
друг с другом (рис. 26, б).
Турбулентным называют
режим, при котором наблюдается
беспорядочное движение, когда частицы
жидкости движутся по сложным траекториям
и слои жидкости постоянно перемешиваются
друг с другом (рис. 26, б).
Ч исло
Рейнольдса есть мера отношения сил
инерции,
действующих в потоке, к силам
вязкости.
Также число Рейнольдса можно рассматривать
как отношение кинетической
энергии жидкости к
потерям энергии на характерной длине
Если у потока число Рейнольдса достаточно
большое (выше критической величины), то
жидкость можно рассматривать как
идеальную. В таком случае вязкостью
можно пренебречь.
исло
Рейнольдса есть мера отношения сил
инерции,
действующих в потоке, к силам
вязкости.
Также число Рейнольдса можно рассматривать
как отношение кинетической
энергии жидкости к
потерям энергии на характерной длине
Если у потока число Рейнольдса достаточно
большое (выше критической величины), то
жидкость можно рассматривать как
идеальную. В таком случае вязкостью
можно пренебречь.
Для каждого вида течения существует критическое число Рейнольдса, которое, как принято считать, определяет переход от ламинарного течения к турбулентному. При течение происходит в ламинарном режиме, при возможно возникновение турбулентности. Критическое значение числа Рейнольдса зависит от конкретного вида течения (течение в круглой трубе, обтекание шара и т. п.), различными возмущениями потока, такими как изменение направленности и модуля вектора скорости потока, шероховатость стенок, близость местных сопротивлений Значения Re выше критического и до определённого предела относятся к переходному (смешанному) режиму течения жидкости, когда турбулентное течение более вероятно, но ламинарное иногда тоже наблюдается — то есть неустойчивая турбулентность.
16
a – коэффициент Кориолиса, учитывающий неравномерность распределения скоростей по сечению потока (или корректив кинетической энергии).
Безразмерный коэффициент a представляет собой отношение действительной кинетической энергии потока к кинетической энергии, вычисленной по средней скорости. Если эпюра скоростей в сечении потока близка к прямоугольной, т.е. скорости в разных точках близки к средней, то коэффициент Кориолиса a близок к единице. Если же скорости в сечении значительно различаются между собой, то и коэффициент a оказывается значительно больше единицы.
Ламинарным называют слоистое течение без перемешивания частиц жидкости и без пульсаций скоростей и давлений. При ламинарном движении жидкости в прямой трубе постоянного сечения все линии тока направлены параллельно оси трубы, то есть поперечные перемещения жидкости отсутствуют. Такое движение является вполне упорядоченным и при постоянном давлении строго установившимся.
Турбулентным называют течение, сопровождающееся интенсивным перемешиванием жидкости и пульсациями скоростей и давлений. При таком движении векторы скоростей имеют не только осевые, но и нормальные к оси трубы составляющие, поэтому вместе с основным продольным движением жидкости вдоль трубы происходят поперечные перемещения (перемешивание) и вращение отдельных объемов жидкости. Этим объясняются пульсации скоростей и давлений.
17
Потери на трение по длине — возникают при равномерном течении, в чистом виде — в прямых трубах постоянного сечения, они пропорциональны длине трубы;
вычисляются по формуле Дарси-Вейсбаха
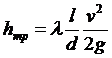 ,
где l-
расстояние между рассматриваемыми
сечениями, т.е. длина трубы, v -
скорость течения, d-
внутренний диаметр трубы,
,
где l-
расстояние между рассматриваемыми
сечениями, т.е. длина трубы, v -
скорость течения, d-
внутренний диаметр трубы, ![]() -
коэффициент гидравлических потерь на
трение по длине,
-
коэффициент гидравлических потерь на
трение по длине, 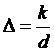 -
относительная шероховатость.
-
относительная шероховатость.
Для ламинарного режима движения жидкости
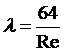 .
.
Основные два вопроса, которые интересуют инженера при рассмотрении турбулентного движения жидкости в трубах:
1) определение потерь напора,
2) распределение скоростей по поперечному сечению трубы.
Потери напора и распределение скоростей могут сильно меняться в зависимости от диаметра трубы, скорости движения, вязкости жидкости и шероховатости стенок труб.
 Для
учета шероховатости используют понятие
относительной шероховатости:
Для
учета шероховатости используют понятие
относительной шероховатости:
.
18
Для
гидравлически
шероховатых труб формула превращается
в формулу Шифринсона
![]() .Так
как в последнем случае коэффициент
гидравлического трения не зависит от
скорости движения воды, то из
формулы
.Так
как в последнем случае коэффициент
гидравлического трения не зависит от
скорости движения воды, то из
формулы ![]() следует,
что потери напора пропорциональны
квадрату скорости
следует,
что потери напора пропорциональны
квадрату скорости![]() .
.
Для
гидравлически
гладких труб наибольшее распространение
получила формула Блазиуса
![]() .С
учетом зависимости
и
того, что
.С
учетом зависимости
и
того, что![]() ,
легко убедиться, что потери напора для
гидравлически гладких труб пропорциональны
скорости в степени 1,75.
,
легко убедиться, что потери напора для
гидравлически гладких труб пропорциональны
скорости в степени 1,75.![]() ,kгл–
коэффициент пропорциональности.
,kгл–
коэффициент пропорциональности.
19
Местными гидравлическими сопротивлениями называются участки трубопроводов (каналов), на которых поток жидкости претерпевает деформацию вследствие изменения размеров или формы сечения, либо направления движения. Местные потери напора вызываются сопротивлениями в арматуре, фасонных частях и оборудовании, вследствие сужения и расширения потока, изменения направления движения жидкости, слияния и разделения потока и т. п.
Местные
потери напора определяют как произведение
скоростного напора непосредственно
вблизи местного сопротивления ![]() , по
формуле
, по
формуле
![]() .
.
Потери
напора на трение по длине определяют
по формуле
 Таким
образом, потери напора в диффузоре
равны
сумме потерь на расширение и на трение
по
длине
Таким
образом, потери напора в диффузоре
равны
сумме потерь на расширение и на трение
по
длине
![]() .
.
Формула Борда — это эмпирическая формула, описывающая потери энергии (или напора) жидкости, происходящие при местном расширении потока.
![]() где
ΔE —
потеря энергии жидкостью;
где
ΔE —
потеря энергии жидкостью;
ξ — эмпирический безразмерный коэффициент потерь, принимающий значения в интервале от нуля до единицы, 0 ≤ ξ ≤ 1;
ρ — плотность жидкости;
V1 и V2 — средняя скорость потока, соответственно, перед и за местным расширением потока.
20
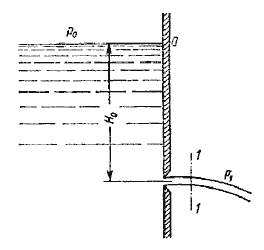 Рассмотрим
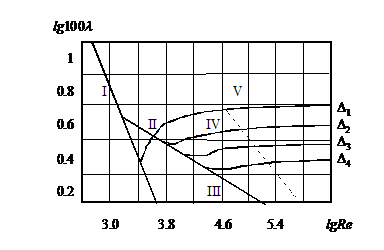
большой резервуар с жидкостью под
давлением Р0,
имеющий малое круглое отверстие в стенке
на достаточно большой глубине Н0 от
свободной поверхности (рис.5.1).
Рассмотрим
большой резервуар с жидкостью под
давлением Р0,
имеющий малое круглое отверстие в стенке
на достаточно большой глубине Н0 от
свободной поверхности (рис.5.1).
Рис. 5.1. Истечение из резервуара через малое отверстие
Жидкость вытекает в воздушное пространство с давлением Р1. Пусть отверстие имеет форму, показанную на рис.5.2, а, т.е. выполнено в виде сверления в тонкой стенке без обработки входной кромки или имеет форму, показанную на рис.5.2, б, т.е. выполнено в толстой стенке, но с заострением входной кромки с внешней стороны. Струя, отрываясь от кромки отверстия, несколько сжимается (рис.5.2, а). Такое сжатие обусловлено движением жидкости от различных направлений, в том числе и от радиального движения по стенке, к осевому движению в струе.
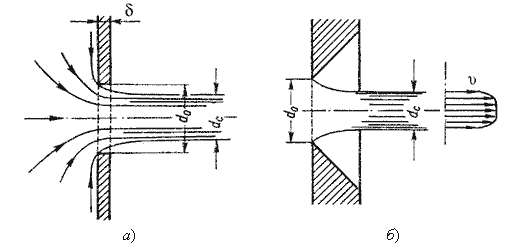 Рис.
5.2. Истечение через круглое отверстие
Рис.
5.2. Истечение через круглое отверстие
Скорость истечения жидкости через отверстие такое отверстие
![]() ,
где
Н -
напор жидкости, определяется как
,
где
Н -
напор жидкости, определяется как
![]() Расход
жидкости определяется как произведение
действительной скорости истечения на
фактическую площадь сечения:
Расход
жидкости определяется как произведение
действительной скорости истечения на
фактическую площадь сечения:
![]()
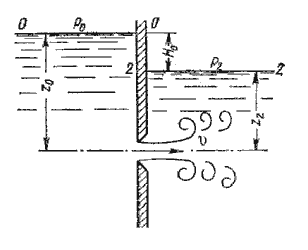 Часто
приходится иметь дело с истечением
жидкости не в атмосферу, а в пространство,
заполненное этой же жидкостью (рис.5.6).
такой случай называется истечением
под уровень,
или истечением через затопленное
отверстие
Часто
приходится иметь дело с истечением
жидкости не в атмосферу, а в пространство,
заполненное этой же жидкостью (рис.5.6).
такой случай называется истечением
под уровень,
или истечением через затопленное
отверстие
В этом случае вся кинетическая энергия струи теряется на вихреобразование, как при внезапном расширении.
Скорость истечения в сжатом сечении струи
где
φ -коэффициент скорости;
Н -
расчетный напор,
![]()
Расход
жидкости равен![]()
Таким образом, имеем те же расчетные формулы, что и при истечении в воздух (газ), только расчетный напор Н в данном случае представляет собой разность гидростатических напоров по обе стенки, т.е. скорость и расход жидкости в данном случае не зависят от высот расположения отверстия.Коэффициенты сжатия и расхода при истечении под уровень можно принимать те же, что и при истечении в воздушную среду.
Формула расхода (для трубы круглого сечения): Q = (Πd²/4)·w Q – расход перекачиваемой жидкости, м3/с d – диаметр трубопровода, м w – скорость потока, м/с
21
Отверстие считают малым, когда его вертикальные размеры d < 0,1Н. Большим отверстием будем считать такое отверстие, для которого тот же d> 0,1Н.
Рассматривая истечение через малое отверстие, практически пренебрегли различием скоростей в разных точках сечения струи. В этом случае поступить так же мы не сможем.
Задача та же: определить расход и скорости в сжатом сечении.
Поэтому расход определяют следующим способом: выделяют бесконечно малую горизонтальную высоту dz. Таким образом, получается горизонтальная полоса с переменной длиной bz. Тогда, интегрировав по длине, можно найти элементарный расход
![]()
где Z – переменный напор по высоте отверстия, на такую глубину погружен верх выбранной полосы;
? – коэффициент расхода через отверстие;
bz – переменная длина (или ширина) полосы.
Расход Q (1) можем определить, если ? = const и известна формула bz= f(z). В общем случае, расход определяют по формуле
![]()
Если форма отверстия прямоугольная, то bz= b = const, интегрировав (2), получаем:
![]()
где Н1, Н2 – напоры на уровнях соответственно у верхней и у нижней кромок отверстия;
Нц – напор над центром отверстия;
d – высота прямоугольника.
Формула
(3) имеет более упрощенный вид:![]()
В зависимости от расположения отверстия различают следующие виды сжатия (рис. 40):
1) полное сжатие со всех сторон (отверстия 1 и 2);
2 ) неполное,
когда сжатия нет
с одной или нескольких
сторон (отверстия 3, 4 и
5).
) неполное,
когда сжатия нет
с одной или нескольких
сторон (отверстия 3, 4 и
5).
Полное сжатие подразделяют на:
а)
совершенное, когда ![]() и
и ![]() (отверстие
1);
(отверстие
1);
б)
несовершенное, когда ![]() и
и ![]() (отверстие
2).
(отверстие
2).
Форма сечения струи жидкости при истечении претерпевает изменения.
Эти изменения называются инверсией. Инверсия происходит вследствие того, что скорости подхода к отверстию в разных точках его периметра различны и вследствие сил поверхностного натяжения. На рис. 41 показано изменение формы струи при истечении через квадратное отверстие по мере удаления от резервуара.
При
несовершенном сжатии
коэффициент расхода ![]() вычисляют
по формулам:
вычисляют
по формулам:
д ля
круглых отверстий
ля
круглых отверстий
![]() (131)
(131)
для прямоугольных отверстий
![]() (132)
(132)
где ![]() –
значение коэффициента расхода при
совершенном сжатии;
–
значение коэффициента расхода при
совершенном сжатии; ![]() и
и ![]() –
поправочные коэффициенты, зависящие
от отношения площади сечения отверстий
–
поправочные коэффициенты, зависящие
от отношения площади сечения отверстий ![]() к
площади сечения сосуда
к
площади сечения сосуда ![]() .
Значения этих коэффициентов принимают
по таблице:
.
Значения этих коэффициентов принимают
по таблице:
Значение величин и при несовершенном сжатии
|
0,10 |
0,20 |
0,30 |
0,40 |
0,50 |
0,60 |
0,70 |
0,80 |
0,90 |
1,00 |
|
0,014 |
0,034 |
0,059 |
0,092 |
0,134 |
0,189 |
0,26 |
0,351 |
0,471 |
0,631 |
|
0,019 |
0,042 |
0,071 |
0,107 |
0,152 |
0,208 |
0,278 |
0,365 |
0,473 |
0,608 |
При неполном сжатии коэффициент расхода вычисляют по уравнениям:
для круглых отверстий
![]() ;
(133)
;
(133)
для прямоугольных отверстий
![]() ,
(134)
,
(134)
где
–
коэффициент расхода при полном
сжатии; ![]() – часть
периметра, на котором нет сжатия; Р
– полный
периметр отверстия.
– часть
периметра, на котором нет сжатия; Р
– полный
периметр отверстия.
При расчете больших отверстий значения коэффициентов расхода, рекомендованных Н. Н. Павловским, приведены в таблице:
Значения коэффициентов расхода для больших отверстий
Виды отверстий и характер сжатия струи |
коэффициент расхода |
Большие отверстия с несовершенным, но всесторонним сжатием ................................................. |
0,70 |
Большие отверстия с умеренным боковым сжатием, без сжатия по дну .......................................................... |
0,80 |
Средние отверстия (шириной до 2 м) с весьма слабым боковым сжатием, без сжатия по дну ………. |
0,90 |
Большие отверстия (шириной 5-6 м) с весьма слабым боковым сжатием, без сжатия по дну ………… |
0,95 |
22
Насадки бывают трех типов: цилиндрические внешние (рис. 8.6, а) и внутренние (рис. 8.6, б), конически сходящиеся (рис. 8.6, в) и расходящиеся (рис. 8.6, г), коноидальные (рис. 8.6, д). Все насадки, как и отверстия, могут работать в затопленном и незатопленном режиме, истечение жидкости через них может быть как при постоянном напоре, так и при переменном.
Расход для всех типов насадков определяется по тем же зависимостям, что и для отверстий в тонкой стенке. Для затопленных насадков расход при постоянном напоре равен:
Q=mw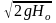 ,
где
Ho
–
напор над центром тяжести выходного
отверстия с учетом скорости подхода;
m=
ej
– коэффициент расхода, зависящий от
типа насадка (табл. 8.2).
,
где
Ho
–
напор над центром тяжести выходного
отверстия с учетом скорости подхода;
m=
ej
– коэффициент расхода, зависящий от
типа насадка (табл. 8.2).
Коэффициенты e, j, m и X для различных типов насадков
Тип насадка и отверстия |
e |
j |
m |
|
Круглое отверстие в тонкой стенке |
0,64 |
0,97 |
0,62 |
0,06 |
Цилиндрический внешний насадок (Вентури) |
1,0 |
0,82 |
0,82 |
0,49 |
Цилиндрический внутренний насадок (Борда) |
1,0 |
0,707 |
0,707 |
1.0 |
Конически расходящийся насадок b=5…70 |
1,0 |
0,45 |
0,45 |
3,94 |
Конически сходящийся насадок b=13о24’ |
0,98 |
0,96 |
0,94 |
0,06 |
Коноидальный насадок |
1,0 |
0,98 |
0,98 |
0,06 |
23
Расход для всех типов насадков определяется по тем же зависимостям, что и для отверстий в тонкой стенке. Для затопленных насадков расход при постоянном напоре равен:
Q=mw , где Ho – напор над центром тяжести выходного отверстия с учетом скорости подхода; m= ej – коэффициент расхода, зависящий от типа насадка (табл. 8.2).
Истечение жидкости из коротких труб. Короткие трубы рассчитывают так же, как цилиндрические насадки, но коэффициенты μ и φ должны учитывать и потери напора по длине. Коэффициенты расхода и скорости в этом случае называют коэффициентами системы. Как и для цилиндрического насадка, сжатие струи на выходе отсутствует, а поэтому μс = φс. Потери напора определяются как сумма потерь напора по длине и местных потерь:
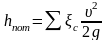 .
(8.35)
.
(8.35)
Коэффициенты
расхода для незатопленных труб
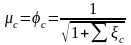 ;
;
для
затопленных
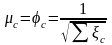 ,
где
,
где
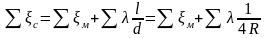 ,
где R=
,
где R=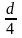 - гидравлический
радиус.
- гидравлический
радиус.
Коэффициенты гидравлического трения λ вычисляются либо по графику Никурадзе, либо по соответствующим формулам, приведенным выше.
24
Расчет
напорных трубопроводов и дюкеров
сводится к выбору экономичных диаметров
трубопроводов и определению потерь
напора. Диаметр трубопровода вычисляют
из формулы постоянства расхода
![]() по
расчетному расходу q, задаваясь
экономичными скоростями
течения v, рекомендуемыми
в курсе
«Водоснабжение» и связанными соотношениями:
по
расчетному расходу q, задаваясь
экономичными скоростями
течения v, рекомендуемыми
в курсе
«Водоснабжение» и связанными соотношениями:
![]()
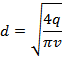
![]() где
где
![]() —
максимальный расчетный расход сточных
вод, м3/с;
—
максимальный расчетный расход сточных
вод, м3/с;
![]() —
площадь живого сечения потока, м2
—
площадь живого сечения потока, м2
![]() —
средняя скорость движения потока, м/с;
—
средняя скорость движения потока, м/с;
Полная
потеря напора в напорном трубопроводе
H состоит из потери на трение по длине
труб
![]() и
суммы потерь на преодоление местных
сопротивлений
и
суммы потерь на преодоление местных
сопротивлений
![]() ,
т. е.
,
т. е.
![]()
Потери
напора на трение по длине составляют:
![]() Где
Где
![]() —
длина трубопровода, м;
—
длина трубопровода, м;
![]() —
единичная потеря напора или гидравлический
уклон;
—
единичная потеря напора или гидравлический
уклон;
![]() —коэффициент
сопротивления трению.
—коэффициент
сопротивления трению.
При
движении сточных вод в условиях
шероховатой зоны турбулентного
режима потери напора по длине рекомендуется
определять по формуле:
![]()
25
Рассмотрим короткий трубопровод с местным сопротивлением, присоединенным к резервуару, заполненному жидкостью. Истечение жидкости в атмосферу из трубопровода длиной l и диаметром d происходит под постоянным напором H ( рис. 49 ).
П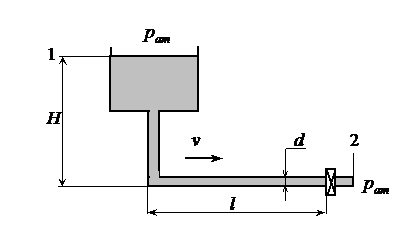 ри
заданных длине l и
диаметре трубопровода d необходимо
определить скорость движения жидкости v и
расход Q.
ри
заданных длине l и
диаметре трубопровода d необходимо
определить скорость движения жидкости v и
расход Q.
Составим
уравнение Бернулли для сечений 1 и 2. При
этом считаем, что ![]() и
и ![]() .
.
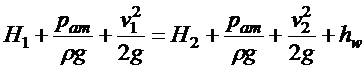 или
или![]() ,где hw -
суммарные (местные и по длине) потери
напора между сечениями 1 и 2, которые
можно представить в виде зависимости
,где hw -
суммарные (местные и по длине) потери
напора между сечениями 1 и 2, которые
можно представить в виде зависимости
![]() ,где
,где![]() .Формулу
можно записать в следующем виде
.Формулу
можно записать в следующем виде![]() .
.
Отсюда
найдем скорость истечения![]() ,где j -
коэффициент скорости.
,где j -
коэффициент скорости.
Расход, пропускаемый коротким трубопроводом
![]() .
.
26
Расчет оптимального диаметра трубопровода – сложная задача, требующая технико-экономических расчетов и учета множества частных факторов. Это связано с тесной взаимосвязанностью параметров проектируемого трубопровода и потока перекачиваемой по нему среды. Увеличение скорости перекачиваемой среды позволяет уменьшить необходимый для поддержания заданного расхода диаметр трубопровода, что снижает его материалоемкость, облегчает и удешевляет монтаж системы. В то же время увеличение скорости неизбежно влечет за собой потери напора, требующие дополнительных затрат энергии на перекачку среды. Чрезмерное снижение скорости так же может повлечь за собой нежелательные последствия.
Формула для расчета оптимального диаметра трубопровода основана на формуле для расхода (для трубы круглого сечения):
Q = (Πd²/4)·w
Q – расход перекачиваемой жидкости, м3/с d – диаметр трубопровода, м w – скорость потока, м/с
Итоговая расчетная формула для оптимального диаметра трубопровода выглядит следующим образом:
d = √(4Q/Πw)
Q – расход перекачиваемой жидкости, м3/с d – диаметр трубопровода, м w – скорость потока, м/с
27-28
Разветвленные (тупиковые) водопроводные сети рассчитывают как системы последовательно соединенных трубопроводов, осуществляющих подачу воды в виде сосредоточенных расходов в боковых ответвлениях (рис.11).

Расчет начинают с линии, идущей от начала сети до самой невыгодной точки (наиболее удаленной и высоко расположенной). Допустим, что на указанной выше схеме невыгодной точкой будет точка 8, тогда основной расчетной линией будет линия 1-2-5-7-8. Расчет этой линии ведут от конечных точек к начальным в такой последовательности: 8-7, 7-5, 5-2 и 2-1.
Зная расчетные расходы воды на каждом участке этой линии, подбирают диаметры труб исходя из скорости и определяют потери напора на отдельных участках, а затем и по всей длине по формуле
![]() Или
Или![]() ,
,
т.е. как сумму потерь напора в последовательно соединенных участках труб.
Если расположение самой невыгодной точки не может быть установлено сразу, рассматривают ряд вариантов расположения основной расчетной линии. После расчета основной линии приступают к расчету ответвлений.
Производим
расчет имеющейся тупиковой сети. Потери
напора определяем по формуле:![]() ,
Где d - поправочный коэффициент, учитывающий
не квадратичность зависимости потерь
напора от средней скорости движения
воды (табл. 1 и 2 приложения 2 СНиП
2.04.01-85*); A - удельное сопротивление труб
(с/м3)2;l - длина участка водопровода, м; Q
- расход воды, м3/с.
,
Где d - поправочный коэффициент, учитывающий
не квадратичность зависимости потерь
напора от средней скорости движения
воды (табл. 1 и 2 приложения 2 СНиП
2.04.01-85*); A - удельное сопротивление труб
(с/м3)2;l - длина участка водопровода, м; Q
- расход воды, м3/с.
![]()
Скорость движения воды по трубопроводу определяем по формуле:
![]() ,где
,где
![]() -
расход воды, м3/с;
-
расход воды, м3/с;
![]() -
площадь живого сечения, м2.
-
площадь живого сечения, м2.
 .
.
Площадь живого сечения определяем по формуле:
![]() ,
где d – внутренний диаметр трубопровода.
,
где d – внутренний диаметр трубопровода.
![]() .
.
При расчете кольцевой водопроводной сети выполняют аналогичные подготовительные работы и расчеты, как и для тупиковых сетей: плановую трассировку, выбор схемы питания (от насосной станции и проходной башни или контррезервуара), определяют удельные, путевые и узловые расходы, намечают начальное потокораспределение и расчетные расходы на случаи: максимального водопотребления, водопотребления в периоды пожаров, максимального транзита воды в контррезервуар при минимальном водопотреблении. После этого приступают к увязке кольцевой сети.
З адачей
увязки кольцевой сети является нахождение
действительного распределения воды по
участкам при принятых наиболее выгодных
диаметрах и расчетных режимах работы
сети. Расчет кольцевых водопроводных
сетей для всех колец и узлов сети должен
удовлетворять следующим условиям
(14.43): в каждом узле должен соблюдаться
баланс расходов (первый закон Кирхгофа);
в каждом кольце и по внешнему контуру
сети суммарные потери напора должны
быть равны нулю (второй закон Кирхгофа):
адачей
увязки кольцевой сети является нахождение
действительного распределения воды по
участкам при принятых наиболее выгодных
диаметрах и расчетных режимах работы
сети. Расчет кольцевых водопроводных
сетей для всех колец и узлов сети должен
удовлетворять следующим условиям
(14.43): в каждом узле должен соблюдаться
баланс расходов (первый закон Кирхгофа);
в каждом кольце и по внешнему контуру
сети суммарные потери напора должны
быть равны нулю (второй закон Кирхгофа):
Рассмотрим, как движется вода в кольцевой сети. Для примера возьмем однокольцевую сеть с питанием в точке 1 (рис. 14.13). Предположим, что узловые отборы воды известны. Для того, чтобы определить расчетные расходы, необходимо знать направление движения воды по отдельным участкам.
 Рис.
14.13. Расчетная схема однокольцевой сети
Рис.
14.13. Расчетная схема однокольцевой сети
Предположим, что поток в точке 1 разделяется на два направления, и в какой-то точке 3 эти потоки сходятся. Следовательно, сумма потерь напора от точки 1 до точки 3 по правой ветви должна равняться сумме потерь напора между этими точками по левой ветви: h1-2 + h2-3 = h1-4 + h4-3.(14.44)
Следовательно, можно сделать вывод о том, что алгебраическая сумма потерь напора по всей длине кольца равна нулю: h1-2 + h2-3 - h1-4 - h4-3, ∑h = 0.(14.45)
Если бы положение точки схода потоков было известно, то расчет кольцевой сети сводился бы к расчету двух тупиков. Но положение точки схода неизвестно, поэтому гидравлический расчет, кроме определения диаметров и потерь напора на всех участках трубопроводов, должен в результате показать и место схода потоков.
29
Водослив — перегораживающая поток часть гидротехнического сооружения, через которую происходит перелив жидкости с одного уровня на другой.
1. По типу порога водослива:
а) водосливы с тонкой стенкой. Струя не прилипает к оголовку.
в) водосливы с широким порогом
- с острой передней кромкой
- с закругленной передней кромкой
г) водослив практического профиля.
Если струя прижимается к сливной грани водослива (давление во всех точках больше атмосферного) – водослив безвакуумного профиля.
2. По типу сопряжения струи с потоком в нижнем бьефе:
а) незатопленные (неподтопленные) водосливы, уровень воды в нижнем бьефе не влияет на расход воды через водослив (рис. 1 – 1); б) затопленные (подтопленные) водосливы; hп = H – z – высота подтопления (глубина подтопления) водослива (у незатопленных водосливов H £ z, hп = 0);
3. В зависимости от соотношения ширины отверстия водослива b и ширины потока B:
а) водосливы без бокового сжатия - b = B ; б) водосливы с боковым сжатием – b < B; bc – ширина струи в сжатом сечении.
4. По геометрической форме водосливного отверстия (рис. 1 – 3):
а) прямоугольные; б) треугольные; в) трапецеидальные; г) круговые; д) параболические и т.д.
Расход через прямоугольный неподтопленный водослив с тонкой стенкой определяется по формуле:
![]() м3/с.
м3/с.
Скорость подхода учтена в коэффициенте расхода водослива m0, поэтому в формуле стоит не H0, а статический напор H.
Прямоугольный неподтопленный водослив с тонкой стенкой без бокового сжатия называется нормальным. Для нормального водослива m0 определяется по эмпирическим формулам:
![]() или
(при Pв³H и H ³ 0,1 м)
или
(при Pв³H и H ³ 0,1 м)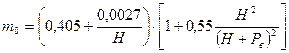 .
.
30
Расход жидкости через прямоугольный водослив с тонкой стенкой можно установить на основе закономерностей истечения жидкости через большие отверстия.
При Н1 = 0 и Н2= Н расход имеет вид
![]() или,
заменяя
или,
заменяя ![]() ,
где
,
где ![]() ‑
коэффициента расхода водослива, получим
‑
коэффициента расхода водослива, получим
![]()
Значения
коэффициента расхода прямоугольного
водослива с тонкой стенкой
без бокового сжатия
изменяются
в пределах ![]()
Для
незатопленного прямоугольного водослива
с тонкой стенкой без бокового сжатия
коэффициент расхода приближенно можно
определять по следующей зависимости,
справедливой при ![]() и
и ![]() .
.
![]()
Водослив практического профиля считается незатопленным, если уровень нижнего бьефа лежит ниже гребня водослива (рис. 17.10).
Коэффициент расхода m для водосливов практического профиля изменяется в широких пределах в зависимости от формы стенки водослива, величины напора и т.д. В качестве средних значений для коэффициента расхода можно принимать следующие:
1. Для водосливов криволинейного профиля
m = 0,45 – 0,49.
2. Для водосливов прямоугольного и полигонального профиля
m = 0,40 – 0,43.
Водосливом с широким порогом называется водослив, имеющий горизонтальный порог, длина которого δ в 2-3 раза превышает напор Н (рис. 17.11). Обычно считается, что на пороге его имеет место плавноизменяющееся движение, близкое к параллельно-струйному.
Коэффициент расхода водослива с широким порогом при отсутствии бокового сжатия изменяется в пределах m = 0,320-0,385 и может быть определен по специальным формулам.
31
Под сопряжением бьефов понимают слияние потока жидкости, переливающегося, например, через водослив в виде струи, с потоком нижнего бьефа.
В результате падения струи скорость потока жидкости увеличивается к низу водослива и наибольшие скорости будут у дна нижнего бьефа. Поток, падающий в нижний бьеф, таким образом, находится в бурном состоянии.
Сопряжение бьефов имеет место при прохождении воды через гидротехнические сооружения (перепад, быстроток, водосброс, щитовой затвор и т.п.) и слиянии с потоком нижнего бьефа.
В практике водоотведения сопряжение бьефов происходит на участке за перепадным колодцем, в зоне изменения уклонов дна коллекторов при переходе от большего уклона дна к меньшему уклону, при выходе потока сточной жидкости из различного вида подпорных сооружений.
При переходе потока из бурного состояния в спокойное возникает гидравлический прыжок. В случае если в нижнем бьефе поток будет находиться в спокойном состоянии, то сопряжение бьефов будет сопровождаться гидравлическим прыжком. В результате слияния потока с верхнего бьефа с нижним могут возникнуть разные формы свободной поверхности:
• сопряжение
с отогнанным гидравлическим прыжком,
когда начало прыжка отодвигается на
расстояние длины отгона ![]() от
сжатой глубины. Линия свободной
поверхности представляет собой кривую
подпора;
от
сжатой глубины. Линия свободной
поверхности представляет собой кривую
подпора;
• сопряжение в виде прыжка в сжатом сечении. При такой форме сопряжения отсутствует длина отгона прыжка и прыжок начинается в сжатом сечении;
• сопряжение бьефов с затопленным гидравлическим прыжком, когда нижний бьеф затапливает прыжок.
32
Гидравлическим ударом называют резкое повышение давления, возникающее в напорном трубопроводе при внезапном торможении потока жидкости. Точнее, это колебательный процесс, возникающий в упругом трубопроводе с капельной жидкостью при внезапном изменении ее скорости. Это явление очень быстротечное и состоит в чередовании резких повышений и понижений давления, связанных с упругой деформацией стенок трубопровода и самой жидкости.
Явление гидравлического удара количественно описал в 1897—1899 г. Н. Е. Жуковский. Увеличение давления при гидравлическом ударе определяется в соответствии с его теорией по формуле:
{\displaystyle
D_{p}=\rho (v_{0}-v_{1})c}
![]() ,где {\displaystyle
D_{p}}
,где {\displaystyle
D_{p}}
![]() —
увеличение давления в Н/м²,{\displaystyle
\rho }
—
увеличение давления в Н/м²,{\displaystyle
\rho }
![]() плотность жидкости
в кг/м³,
плотность жидкости
в кг/м³,
{\displaystyle
v_{0}}
![]() {\displaystyle
v_{1}} —
средние скорости в трубопроводе до и
после закрытия задвижки (запорного
клапана)
в м/с,
{\displaystyle
v_{1}} —
средние скорости в трубопроводе до и
после закрытия задвижки (запорного
клапана)
в м/с,
с — скорость распространения ударной волны вдоль трубопровода.
Эту
формулу можно получить, исходя из закона
сохранения импульса
![]() поперечное
сечение трубопровода.
поперечное
сечение трубопровода.
Жуковский доказал, что скорость распространения ударной волны c находится в прямо пропорциональной зависимости от сжимаемости жидкости, величины деформации стенок трубопровода, определяемой модулем упругости материала E, из которого он выполнен, а также от диаметра трубопровода.
Следовательно, гидравлический удар не может возникнуть в трубопроводе, содержащем газ, так как газ легко сжимаем.
Зависимость
между скоростью ударной волны c,
её длиной и временем распространения
(L и {\displaystyle
\tau }
![]() соответственно)
выражается следующей формулой:{\displaystyle
c=2L/\tau }
соответственно)
выражается следующей формулой:{\displaystyle
c=2L/\tau }
![]()
33
Различают полный и неполный гидроудар. Полный гидроудар предполагает полную остановку жидкости, а при неполном происходит ее торможение до скорости V1.
Гидроудар называют прямым, если фаза гидравлического удара t0 = 2l/c меньше времени закрытия трубопровода: t0 < tзак. Если t0 > tзак, то удар непрямой.
Величина повышения давления в трубопроводе при прямом полном гидравлическом ударе определяется формулой Жуковского:
Dp = rV0 c.
Если удар неполный, то Dp = r(V0 – V1)с.
При непрямом гидравлическом ударе можно пользоваться приближенными формулами:
для полного удара
 ;
;для неполного удара
 .
.
Как можно легко увидеть, наибольшую опасность представляет прямой полный гидроудар.
34
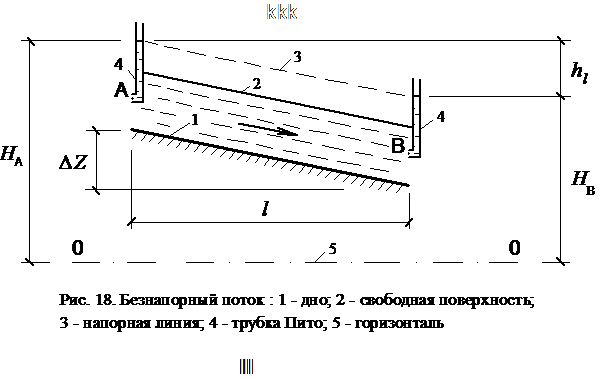 Расчёт
безнапорных потоков состоит в решении
совместной задачи о пропуске расхода q при
допустимых скоростях потока V и
геометрических уклонах iгеом дна
труб, каналов и т.д. Безнапорные (со
свободной поверхностью) потоки наблюдаются
в канализационных трубах, дорожных
лотках, каналах; в природе — в реках,
ручьях.
Расчёт
безнапорных потоков состоит в решении
совместной задачи о пропуске расхода q при
допустимых скоростях потока V и
геометрических уклонах iгеом дна
труб, каналов и т.д. Безнапорные (со
свободной поверхностью) потоки наблюдаются
в канализационных трубах, дорожных
лотках, каналах; в природе — в реках,
ручьях.
Для расчёта безнапорных потоков широко применяют формулу Шезú для определения геометрического уклона дна трубопровода, канала или траншеи
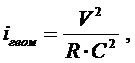 (38)
(38)
где R — гидравлический радиус (м); С — коэффициент Шезú. ( сопротивления трения по длине )
Коэффициент Шезú с достаточной для практики точностью можно определить по формуле Маннинга
![]() (39)
(39)
где n — коэффициент шероховатости стенок трубы или канала (величина, численно характеризующая сопротивление, оказываемое руслом протекающему потоку) ; R — гидравлический радиус, подставляемый в метрах!
35