ЗАВДАННЯ ДЛЯ КОНТРОЛЬНОЇ РОБОТИ 1
Завдання 1-10. Визначити реакції стрижнів, що утримують грузи F1 і F2. Масою стрижнів нехтувати. Схему свого варіанту див. на мал. 4. Числові дані свого варіанту узяти з табл. 2.
Мал. 4
Таблиця 2 (до задач 1—10)
-
№ завдання та схеми на мал. 4
F1
F2
1
2
3
4
5
6
7
8
9
10
Варіанти
кН
00
10
20
30
49
59
62
70
80
90
01
11
21
31
40
58
60
75
85
91
02
12
22
32
41
57
63
71
81
92
03
13
23
33
42
56
61
76
86
93
04
14
24
34
43
55
66
72
82
94
05
15
25
35
44
54
64
77
87
95
06
16
26
36
45
53
67
73
83
96
07
17
27
37
46
52
65
78
88
97
08
18
28
38
47
51
69
74
84
98
09
19
29
39
48
50
68
79
89
99
0,4
0,3
0,6
0,2
0,5
0,8
0,4
1,2
0,8
0,9
0,5
0,8
0,4
0,5
0,8
0,4
0,2
0,8
1,0
0,6
Завдання 11-20. Визначити реакції опор двохопорної балки (мал. 5). Дані свого варіанту узяти з табл. 3.
Мал. 5
Таблиця 3 (до задач 11—20)
№ завданя; № схеми на мал..5 |
Варіант |
q |
F |
M |
№ авдання; № схеми на мал. 5 |
Варіант |
q |
F |
M |
Н/м |
Н |
Н*м |
Н/м |
Н |
Н*м |
||||
11;1 |
00 11 22 33 45 50 66 71 84 99 |
5 2 10 1,5 6 3 8 4,5 1 12 |
40 12 16 50 82 15 45 18 20 54 |
10 20 14 30 6 25 40 10 25 35 |
12;2 |
01 12 23 34 46 51 67 72 88 90 |
1 4,5 2 5 3,5 6 3 1,5 8 10 |
60 20 15 2,5 40 35 100 80 30 50 |
54 85 40 100 55 60 90 20 75 30 |
13;3 |
02 13 24 35 47 52 68 73 80 91 |
5 2,5 4 10 12 8 4,5 2 6 3,5 |
80 15 30 55 10 100 65 85 90 20 |
25 10 20 40 15 30 45 60 18 16 |
14;4 |
03 14 25 36 48 53 69 74 85 92 |
4 1 12 8 2 14 6 10 16 20 |
10 12 16 20 5 30 25 8 4 15 |
8 10 15 12 3 24 20 6 12 8 |
15;5 |
04 15 26 37 49 54 60 75 81 93 |
5 4,5 8 1,5 2,5 10 12 15 5,5 6 |
50 35 25 10 65 8 16 30 12 55 |
35 30 20 8 50 25 40 28 15 45 |
16;6 |
05 16 27 38 40 55 61 76 86 94 |
8 3,5 0,5 10 15 4,5 8 12 8,5 6 |
12 10 8 15 18 20 3 5 12 4 |
20 45 10 50 30 15 25 18 30 45 |
17;7 |
06 17 28 39 41 56 62 77 82 95 |
2 4 6 8 12 10 20 14 16 30 |
50 10 12 15 80 35 40 25 14 65 |
35 5 8 50 15 25 30 20 65 75 |
18;8 |
07 18 29 30 42 57 63 78 87 96 |
4 6,5 10 2,5 12 3 8 1,5 1 5 |
18 24 16 20 40 35 10 12 60 15 |
15 20 12 25 50 65 25 90 35 10 |
19;9 |
08 19 20 31 43 58 64 79 83 97 |
4 1,5 1 10 5 8 6 12 3 7 |
15 40 20 16 18 10 25 40 35 12 |
2 15 18 25 14 35 20 30 15 10 |
20;10 |
09 10 21 32 44 59 65 70 88 98 |
4 6 2 18 20 10 16 8 14 30 |
50 65 80 10 55 30 10 2 6 50 |
10 8 100 15 150 45 25 40 10 60 |
Завдання 31-40
Завдання 31. Точка почала рівноприскорений рух із стану спокою по прямій і через 5 с придбала швидкість v = 10 м/с. З цієї миті точка почала рухатися по колу радіусу r = 50 м. Рухаючись по колу, точка перші 15 с здійснювала рівномірний рух, потім впродовж 10 с рухалася рівноуповільнено до зупинки
Визначити: 1) середню швидкість руху точки на усьому шляху; 2) значення повного прискорення точки через 5с після початку рівноуповільненого руху.
Завдання 32. Шків діаметром d = 400 мм протягом 10 с обертався з постійною кутовою швидкістю ωo = 8 рад/с. Потім став обертатися рівноприскорено і через 12 с рівноприскореного обертання його кутова швидкість досягла ω1= 14 рад/с.
Визначити: 1) число обертів і середню кутову швидкість за весь час обертання; 2) окружну швидкість точок, розташованих на ободі шківа, через 6 с після початку рівноприскореного руху.
Завдання 33. Точка почала рухатися рівноприскорено із стану спокою по колу радіусом r = 100 м і через 10 c придбала швидкість v = 20 м/с. З цієї миті точка 15 c рухалася одночасно по колу, після чого стала рухатися по прямій і через 5 c рівноуповільненого руху по прямій зупинилася.
Визначити: I) середню швидкість руху точки на усьому шляху; 2) значення повного прискорення точки через 5 с після початку руху.
Завдання 34. Вал діаметром d = 500 мм впродовж 5 с обертався з постійною кутовою швидкістю ωo = 20 рад/с, після чого став уповільнювати своє обертання з постійним кутовим прискоренням. Через 10 с після початку рівноуповільненого обертання кутова швидкість валу стала ω1= 10 рад/с.
Визначити: I) число обертів і середню кутову швидкість валу за весь час
обертання; 2) окружну швидкість точок, розташованих на поверхні валу, через 4 с після початку рівноуповільненого обертання.
Завдання 35. Точка почала рухатися рівноприскорено по дузі кола радіусом r=50 м з стану спокою і через 20 с придбала швидкість v= 20 м/с. З цього моменту точка стала рухатися прямолінійно, причому перші 5 с рівномірно, а подальші 5 с - рівноуповільнено до зупинки.
Визначити: 1) середню швидкість руху точки на усьому шляху. 2) значення повного прискорення точки через 10 с після початку її руху.
Завдання
36. Тіло,
уповільнюючи обертання з постійним
кутовим прискоренням
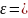2
рад/с2
через 14 с знизило свою кутову швидкість
до величини ω
= 12 рад/с, після
чого оберталося рівномірно з цією
кутовою швидкістю впродовж 10 с.
Визначити: 1) число обертів і середню кутову швидкість за весь час обертання; 2) окружну швидкість точок тіла, розташованих на відстані r = 1 м від вісі його обертання за 4 с до початку рівномірного обертання.
Завдання 37. Перші 5 с точка рухалася рівномірно по колу радіусом r = 50 м зі швидкістю v=20 м/с. У подальші 10 с, рухаючись рівноуповільнено по тому ж колу, знизила свою швидкість до 10 м/с і з цією швидкістю точка почала рівноуповільнено рухатися по прямій до повної зупинки.
Визначити: 1) середню швидкість руху точки на усьому шляху; 2) повне прискорення точки після початку рівноуповільненого руху.
Завдання
38. Ротор:
діаметром d =200 мм почав обертання із
стану спокою з постійним кутовим
прискоренням
=
4 рад/с2
і через деякий час досяг кутової швидкості
ω =
40 рад/с, після чого з цією кутовою
швидкістю зробив 510 обертів.
Визначити: I) число обертів і середню кутову швидкість за весь час обертання; 2) окружну швидкість точок, розташованих на поверхні ротора, через 8 с після початку обертання.
Завдання 39. Точка, рухаючись прямолінійно і рівноприскорено із стану спокою, пройшла шлях в 100 м і придбала швидкість ω =20 м/с. З цією швидкістю точка продовжувала прямолінійний рух впродовж 5 с. Після цього точка почала рухатися по колу радіусом r = 40 м і 20 с рухалася рівноуповільнено до повної зупинки.
Визначити: 1) середню швидкість руху точки на усьому шляху; 2) повне прискорення точки через 10 с після початку її рівноуповільненого руху по колу.
Завдання 40. Двигун, ротор якого обертався з частотою 430 об/хв, був відключений від джерела живлення і через 40 с знову підключений до джерела струму. За цей час при рівноуповільненому обертанні ротора його кутова швидкість знизилася до 5 рад/с. Після подання електроенергії ротор двигуна, обертаючись рівноприскорено, через 10 с знову став обертатися з частотою 430 об/хв.
Визначити; I) число обертів і середню кутову швидкість за весь час рівноуповільненого і рівноприскореного обертання ротора двигуна; 2) окружну швидкість точок, розташованих на поверхні ротора, через 30 с після відключення джерела струму, якщо діаметр ротора d = 200 мм.