
- •Дослідження насоса-дозатора з півдсилювачем потоку. Розроблення математичної моделі
- •1 Сучасний стан розвитку систем гідрооб’ємного рульового керування сільськогосподарських машин
- •1.1 Огляд гідросистем гідрообємного рульового керування та методів
- •1.2 Аналіз методів досліджень систем гідрообємного рульового керування
- •1.3 Висновки, мета і задачі роботи
- •2.1 Аналіз гідравлічної схеми насоса-дозатора з вбудованим підсилювачем потоку
- •2.2.1 Розробка розрахункової схеми системи
- •2.2.2 Розроблення рівнянь балансу витрат
- •2.2.3 Аналіз складових рівнянь балансу витрат
- •2.2.4 Розроблення рівнянь руху механічних ланок
- •2.2.5 Аналіз складових рівнянь руху механічних ланок
- •2.2.6 Перетворення рівнянь
- •3 Просторове моделювання машини
- •3.1 Аналіз роботи деталі
- •3.2 Огляд існуючих програм комп’ютерного проектування та вибір програмного середовища для вирішення поставленої задачі
2.2.3 Аналіз складових рівнянь балансу витрат
Нижче розглядаються закони фізики, які дозволяють визначити складові рівнянь (2.1) – (2.10). Витрати крізь дросельні кромки золотникової пари визначаються з умови, що при проектуванні цих кромок закладається умова турбулентного режиму течії робочої рідини як така, що не змінює характеристик дроселя при зміні температури рідини. Відповідно до прийнятої квадратичної залежності таких витрат від перепаду тиску, вони можуть бути визначені за залежністю [46, 70]
 ,
(2.12)
,
(2.12)
де μ – коефіцієнт витрати робочої рідини;
ρ – густина робочої рідини;
fi (Δφ) – площа дросельної кромки, яка залежить від неузгодженості Δφ в золотниковій парі;
∆рі – перепад тиску на дросельній кромці, що розглядається. Модуль перепаду тиску під радикалом в сполученні з функцією sign(Δpі) після радикалу дозволяє врахувати миттєвий напрямок течії рідини крізь дросельну кромку.
Площі дроселів визначаються геометрією робочих поверхонь, які утворюють дросель. В запропонованій конструкції насоса-дозатора дроселі f1., f2, f6 та f7 утворюються перетином пазів на золотнику з отворами на гільзі. Кожен перетин утворює сегмент, як показано на рисунку 2.9, а дросельна щілина утворюється декількома рядами пазів і отворів і, крім того, декількома отворами в кожному ряду.

Рисунок 2.3 – Площа сегмента дроселя, який створюється отвором і пазом
При визначенні площі дроселя слід враховувати, що при нейтральному положенні золотникової пари кромка паза та отвору, що утворюють відповідний дросель, знаходяться на відстані позитивного перекриття Li. Враховуючи значно більший діаметр золотника Dz в порівнянні з радіусом ri отворів на гільзі, площу сегмента fi., з невеликою похибкою можна розглядати як площу плоского сегмента. Тоді площа відповідних дроселів з урахуванням позитивного перекриття Lі може бути визначена наступними залежностями:
дроселів підведення та відведення рідини до камер дозуючого вузла
 , (2.13)
, (2.13)
площа дроселя підведення рідини до гідроциліндра f6 може бути визначена залежністю
 , (2.14)
, (2.14)
а площа дроселя відведення рідини з гідроциліндра f7 може бути визначена залежністю
 , (2.15)
, (2.15)
де п1, п6, п7 – кількість рядів отворів, які утворюють відповідний дросель;
k6, k7 – кількість отворів в кожному ряду, які утворюють відповідний дросель;
r1, r6, r7 – радіус отвору, який утворює відповідний дросель;
L1, L6, L7 – позитивне перекриття кромок відповідного дроселя;
αi–
центральний кут сегмента, який згідно
рисунка 2.9 дорівнює
 , (2.16)
, (2.16)
Δx – лінійний вираз відносного зміщення золотника і гільзи внаслідок відносного кутового повороту Δφ. При цьому величини лінійного і кутового зміщень пов'язані співвідношенням
 , (2.17)
, (2.17)
де Dz – діаметр золотника золотникової пари.
В запропонованій конструкції насоса-дозатора дроселі f3., f4 та f5 утворюються перетином росточок в золотнику золотникової пари з отворами на золотнику підсилювача потоку. Кожен перетин утворює сегмент аналогічно, як показано на рисунку 2.9, але зміщення Δx створюється не кутовим поворотом Δφ, а зміщенням x2 золотника підсилювача потоку. Тоді площа цих дроселів з урахуванням позитивного перекриття L3 (конструктивно перекриття однакове для всіх цих дроселів) може бути визначена наступними залежностями:
дроселя підведення рідини від дозуючого вузла до вихідного каналу підсилювача потоку
 , (2.18)
, (2.18)
дроселя підведення рідини від насоса живлення до вихідного каналу підсилювача потоку
 , (2.19)
, (2.19)
вхідного дроселя підсилювача потоку
 , (2.20)
, (2.20)
де п3, п4, п5 – кількість отворів, які утворюють відповідний дросель;
r3, r4 – радіус отвору, який утворює відповідний дросель.
Дросель зливного золотника формується канавками, параметри яких показано на рисунку 2.4. Площа цього дроселя f9 залежить від осьового положення х1 зливного золотника і визначається на кожній характерній ділянці окремим виразом.
|
Рисунок 2.4 – Схема визначення площі робочого вікна зливного золотника |
В цілому така залежність при умові Вфр>rфр може бути описана наступним виразом
 , (2.21)
, (2.21)
де nк – кількість канавок на шийці зливного золотника;
Lфр, Bфр та rфр – довжина, глибина та радіус фрезерованої канавки відповідно до рисунку 2.4;
d1 – діаметр центральної шийки зливного золотника, на якій виконані фрезеровані канавки;
![]() – центральний
кут сегмента радіусної частини канавки,
що дорівнює
– центральний
кут сегмента радіусної частини канавки,
що дорівнює
 . (2.22)
. (2.22)
Площа дроселя f8(Δφ) управління тиском під торцем зливного золотника при зміщенні Δx в золотниковій парі в діапазоні Lуп < Δx< rз+rг формується перетином отвору 41 радіусом rг на гільзі з отвором 40 радіусом rз і канавкою 42 на золотнику і, як це видно на схемі, яку показано на рисунку 2.5,а і 2.5,б, визначається як сума двох складових
f8.(Δφ)= fот+ fкан . (2.23)
де fот - складова площі дроселя від перетину отворів, що його утворюють;
fкан - складова площі дроселя від перетину отвору з канавкою.

а) б) в)
Рисунок 2.5 – Площа дроселя f8(Δφ) управління тиском при зміщенні Δx
в золотниковій парі в діапазоні Lуп < Δx< rз+rг
а) при малих зміщеннях Δx, б) при великих зміщеннях Δx,
в) при дуже великих зміщеннях Δx > rз+rг
Розрахункову схему визначення складової площі fот цього дроселя побудовано на рисунку 2.6, згідно якого ця площа є загальною площею двох отворів і визначається сумою відповідних сегментів
fот = fсег.г + fсег.з . (2.24)
|
Рисунок 2.6 – Розрахункова схема визначення складової площі fот від перетину отворів дроселя управління тиском |
Площа двох сегментів, які утворюють цей дросель, з врахуванням від’ємного перекриття кромок цього дроселя Lуп може бути розрахована за виразом
 , (2.25)
, (2.25)
де rз і rг – радіуси отворів відповідно на золотнику і гільзі, які утворюють даний дросель;
Lуп – від’ємне перекриття кромок цього дроселя, яке дорівнює різниці радіусів отворів дроселя, тобто Lуп = rз – rг ;
αуп , βуп – центральні кути сегментів перетину отворів на гільзі та золотнику відповідно, які визначаються залежностями
 , (2.26)
, (2.26)
 . (2.27)
. (2.27)
Складова площі fкан від перетину отвору 41 з канавкою 42 при різному зміщенні Δx в золотниковій парі визначається різними елементами цієї канавки – горизонтальною та поперечною складовими.
При великих зміщеннях Δx, коли Δx > rз+rг (рисунок 2.5,в), площа fкан визначається виключно площею поперечного перерізу канавки у вигляді трикутника, так як отвори дроселя повністю перекриваються. На рисунку 2.7 зображено розрахункову схему, по якій визначаються параметри поперечного перерізу канавки для визначення її площі.
Згідно зображеної схеми поперечна площа канавки визначається як площа трикутника наступною залежністю
 ,
(2.28)
,
(2.28)
де γк – кут профілю канавки (рисунок 2.7);
h1 и Δφ1 – проміжні параметри, які визначаються за формулами
 ; (2.29)
; (2.29)

Рисунок
2.7 – Площа поперечного перерізу канавки
дроселя управління тиском при Δx
=0 та при

 , (2.30)
, (2.30)
де Rк Нфр – радіус дна і глибина фрезерування канавки на золотнику.
При малих зміщеннях Δx (рис. 2.5,а) площа горизонтальної складової fкан, яка є проекцією частини канавки, що пересіклась з отвором, набагато менша за поперечну складову, яка відповідає максимальній площі трикутника профілю канавки в площині перетину канавки з кромкою отвору на золотнику (переріз Б-Б на рис. 2.7). Тому при таких зміщеннях Δx площа fкан визначається горизонтальною складовою, яка змінюється від нуля при Δx ≤ Lуп.
При
збільшені Δx
в діапазоні
 ,
коли горизонтальна складова площі
канавки fкан
починає перевищувати площу канавки в
поперечному перерізі (рис. 2.5,б), тоді
площа fкан
визначається меншою величиною, тобто
площею поперечного перерізу і відповідає
площі трикутника профілю канавки в
площині перетину канавки з кромкою
отвору на золотнику.
,
коли горизонтальна складова площі
канавки fкан
починає перевищувати площу канавки в
поперечному перерізі (рис. 2.5,б), тоді
площа fкан
визначається меншою величиною, тобто
площею поперечного перерізу і відповідає
площі трикутника профілю канавки в
площині перетину канавки з кромкою
отвору на золотнику.
Але при аналізі витрати рідини крізь дросель управління тиском слід зауважити, що перепад тиску на кромці цього дроселя при Δx в діапазоні різний на різних ділянках. Це пов’язано з тим, що тиск в порожнині канавки буде відрізнятись від тиску в основній порожнині у зв’язку з втратами тиску при протіканні рідини крізь вузький канал. Зміна епюри тиску призводить до різних перепадів тиску на ділянці, утвореній двома отворами, та на ділянці, утвореній отвором і канавкою.
В першому наближенні зміну витрати крізь дросель управління тиском при зміщеннях Δx в діапазоні запропоновано врахувати введенням закону зміни площі канавки fкан. При цьому розглядається площа канавки fкан тільки в поперечному перерізі і ця величина приймається максимальною fкан.мак, що відповідає перерізу Б-Б на рис. 2.7, але додатково вводиться коефіцієнт, який враховує характер зміни витрат в залежності від Δx.
Прийнято лінійний характер зміни витрат крізь цю ділянку дроселя, який змінюється від нуля при Δx = Lуп до максимально можливого при Δx = rз+rг згідно наведеного вище характеру зміни площі цього дроселя та перепаду тиску на ньому. Така зміна врахована коефіцієнтом, що змінюється від нуля до одиниці, і визначається параметрами дроселя залежністю
 (2.31)
(2.31)
де kкан – коефіцієнт, що наближено враховує зміну витрати крізь дросель управління тиском при зміщенні Δx. Графік цього коефіцієнта наведено на рисунку 2.8.
Тоді
площа fкан
при зміщенні Δx
в золотниковій парі в діапазоні
 визначається залежністю
визначається залежністю
|
Рисунок 2.8 – Графік зміни коефіцієнта kкан в діапазоні зміщення Δx в золотниковій парі |
 , (2.32)
, (2.32)
де fкан.мак – максимальна площа трикутної канавки, яка розглядається в площині перетину цієї канавки з кромкою отвору на золотнику,
 (2.33)
(2.33)
Підсумковий вираз для визначення площі fкан у всьому діапазоні зміщень Δx в золотниковій парі має вигляд
 (2.34)
(2.34)
Така реалізація дроселя забезпечує нелінійний характер зміни площі цього дроселя (рис. 2.9), коли при малих зміщеннях Δx він має значну площу, а при зміщеннях Δx більше зони нечутливості в золотниковій парі ця площа суттєво зменшується.
|
Рисунок 2.9 – Графік зміни сумарної площі дроселя управління тиском від лінійного зміщення золотника відносно гільзи fдр.уп.(Δх) |
Під час аналізу витрат розглядаються також витрати рідини, що проходять крізь камери гідроагрегатів, які визначаються законом руху робочого органу гідроагрегату та його геометричними характеристиками.
Витрата рідини, яка проходить крізь камери дозуючого вузла, дорівнює
 , (2.35)
, (2.35)
де qд – робочий об'єм дозуючого вузла,
 – кутова
швидкість обертання ротора.
– кутова
швидкість обертання ротора.
Витрата рідини, що пов'язана з переміщенням поршня виконавчого гідроциліндра, дорівнює
 , (2.36)
, (2.36)
де Fn – ефективна площа поршня виконавчого гідроциліндра,
 –
швидкість
переміщення поршня виконавчого
гідроциліндра.
–
швидкість
переміщення поршня виконавчого
гідроциліндра.
Витрати рідини, пов'язані з переміщенням зливного золотника, дорівнюють
 ; (2.37)
; (2.37)
де dzz– діаметр зливного золотника;
 – швидкість
переміщення зливного золотника.
– швидкість
переміщення зливного золотника.
Витрати рідини, пов'язані з переміщенням зливного золотника, дорівнюють
 ; (2.38)
; (2.38)
де dzp – діаметр зливного золотника;
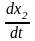 – швидкість
переміщення зливного золотника.
– швидкість
переміщення зливного золотника.
Витрати, які пов'язані з деформацією рідини, що знаходиться в порожнині гідросистеми під тиском рі, через зміни тиску в цій порожнині, визначаються залежністю [15, 12, 18, 21]
 , (2.39)
, (2.39)
де Vi – об’єм порожнини, в якій рідина знаходиться під тиском рі;
Епр(р) – зведений модуль об'ємної пружності, який враховує, що робоча рідина є двофазної сумішшю робочої рідини і нерозчиненого газу. Вивченням залежності Епр(р) займалося багато дослідників як експериментально, так і теоретично. В результаті проведених досліджень [12, 17, 25] показано, що при ізотермічному стисканні ця залежність визначається формулою
 , (2.40)
, (2.40)
де Еж – адіабатичний модуль пружності самої рідини;
 – відносний
об’єм газової фази при нормальних
умовах (р0
= 0,1 МПа, t
= 20°С);
– відносний
об’єм газової фази при нормальних
умовах (р0
= 0,1 МПа, t
= 20°С);
n – показник політропи.
Крім того, під час аналізу витрат розглядаються перетоки через зазори. Згідно прийнятих припущень в зазорах деталей насоса-дозатора виникає ламінарний режим течії і витрати рідини на перетікання крізь зазори будуть пропорційні перепаду тиску в суміжних порожнинах, і визначаються залежністю [12]
 , (2.41)
, (2.41)
де σi – коефіцієнт перетоків для щілини;
Δpi – перепад тиску на щілині.
У випадку, коли зазор утворюється кільцевими концентричними щілинами, як у випадку Qп1 – Qп6, Qп15 – Qп16 та Qп18 – Qп19 , коефіцієнт перетоків визначаються за формулою [12, 25]
 , (2.42)
, (2.42)
де ν та ρ – в'язкість і густина рідини;
di , li та εi – діаметр поверхні, довжина щілини та величина зазору на і-ій ділянці гідросистеми, по якій відбувається перетікання рідини.
Тоді величини перетоків по таким зазорам дорівнюють
 ; (2.43)
; (2.43)
 ; (2.44)
; (2.44)
 ; (2.45)
; (2.45)
 ; (2.46)
; (2.46)
 ; (2.47)
; (2.47)
 ; (2.48)
; (2.48)
 ; (2.49)
; (2.49)
 ; (2.50)
; (2.50)
 ; (2.51)
; (2.51)
 ; (2.52)
; (2.52)
 ; (2.53)
; (2.53)
 ; (2.54)
; (2.54)
де εг.к, εzp та εzz – величина зазору у з’єднанні відповідно гільзи та корпусу, золотника підсилювача потоку та золотника зливу з спряженими поверхнями;
 – прийнятий
коефіцієнт.
– прийнятий
коефіцієнт.
Знак перепаду тисків буде визначати дійсний напрямок перетікання робочої рідини.
У випадку, коли зазор утворюється щілинами, які з деяким припущенням можна прийняти плоскими і паралельними, як у випадку Qр7 – Qр14 та Qpt i Qv, коефіцієнти перетоків визначаються за формулою [12, 25]
 ,
(2.55)
,
(2.55)
де bi та li – ширина та довжина щілини на і-ій ділянці гідросистеми, по якій виникає перетікання рідини.
Тоді величини перетоків по таким зазорам визначаються по наступним формулам
 ; (2.56)
; (2.56)
 ; (2.57)
; (2.57)
 ; (2.58)
; (2.58)
 ; (2.59)
; (2.59)
 ; (2.60)
; (2.60)
 ; (2.61)
; (2.61)
 ; (2.62)
; (2.62)
 ; (2.63)
; (2.63)
 ; (2.64)
; (2.64)
 ,
(2.65)
,
(2.65)
 , (2.66)
, (2.66)
 , (2.67)
, (2.67)
де ni – кількість однотипних елементів (канавок або отворів), по яких відбуваються перетоки;
k2, k2, k4 – коефіцієнти, що враховують зміну довжини кромки при різних її шириеах;
εzp.- зазор в золотниковій парі (золотник-гільза);
εt.- зазор в стиках бокових пластин.




