Задача №7

Стальной стержень длиной l сжимается продольной силой Р.

Требуется:

1. подобрать поперечные размеры стержня при заданном допускаемом напряжении на сжатие [] = 160МПа (расчет проводить методом последовательных приближений);

2. найти величину критической силы и коэффициент запаса устойчивости [n_y];

3. вычертить поперечное сечение стойки в масштабе 1:1.

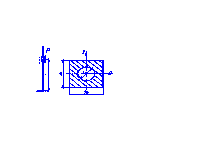
Исходные данные: Р = 5,5кН; l = 0,85м; марка стали – Ст 5.

Решение:

1. Определяем размеры поперечного сечения.

Выразим гибкость стержня через площадь поперечного сечения.

откуда

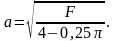
Моменты инерции сечения:

Минимальный радиус инерции сечения:

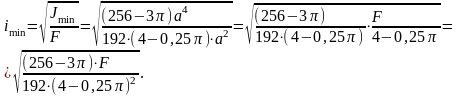
Учитывая, что для заданной схемы закрепления стойки  = 0,5,

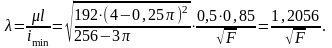
В первом приближении примем коэффициент уменьшения допускаемого напряжения ₁ = 0,5.

м²;

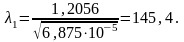
По ₁ определяем табличное значение  для Ст 5:

_1табл = 0,26.

Во втором приближении примем ;

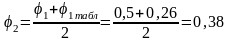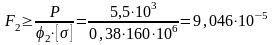м²;

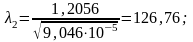
_2табл = 0,34.

В третьем приближении примем ;

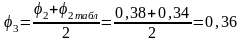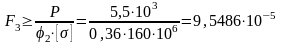м²;

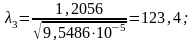
_3табл = 0,36 = ₃.

Окончательно принимаем 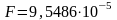м²;

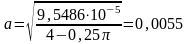м, принимаем а = 6мм.

2. Определим критическую силу.

Так как   _пред = 100, то для определения Р_кр используем формулу Эйлера:

где 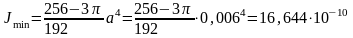м⁴;

Е = 210⁵МПа;

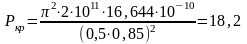кН.

Коэффициент запаса устойчивости:

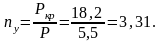
3. Вычертим поперечное сечение в масштабе 4:1.

Задача №8

Клапанная пружина имеет размеры: средний диаметр витка – D, диаметр проволоки пружины d. Сила, сжимающая пружину при закрытии клапана – Р_min, сила, сжимающая пружину в момент полного открытия клапана – Р_max. Материал проволоки пружины – хромованадиевая сталь, имеющая следующие механические характеристики: предел текучести _Т, предел выносливости при симметричном цикле - _-1, предел выносливости при отнулевом (пульсирующем) цикле - ₀.

Пружина имеет эффективный коэффициент концентрации напряжений k_, коэффициент влияния качества обработки поверхности  и масштабный коэффициент _.

Требуется:

1. определить максимально _max и минимальное _min напряжения в проволоке пружины и вычислить коэффициент асимметрии цикла R;

2. найти среднее _m и амплитудное _а напряжения цикла;

3. построить в масштабе схематизированную диаграмму предельных амплитуд (в осях _а и _m), используя механические характеристики стали _-1, ₀ и _Т;

4. вычислить коэффициент запаса прочности и сравнить его с коэффициентом, полученным по диаграмме предельных амплитуд (графически).

Исходные данные: D = 0,048м; d = 0,0037м; Р_max = 150Н; Р_min = 65Н; _Т = 930МПа;

_-1 = 500МПа; ₀ = 790МПа; k_ = 1,08;  = 0,81; _ = 0,98.

Решение:

1. Напряжение в проволоке пружины определяем по формуле:

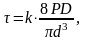
где 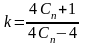- коэффициент, учитывающий кривизну витка и нелинейное распределение касательных напряжений в поперечном сечении витка:

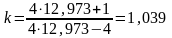
Максимальное и минимальное напряжения в проволоке:

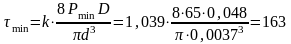МПа;

МПа.

Коэффициент асимметрии цикла:

.

2. Среднее и амплитудно напряжения цикла:

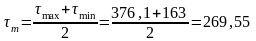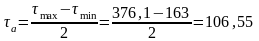МПа;

МПа.

3. Зададимся прямоугольной системой координат _m, _а с началом в точке О (0;0), в которой по оси абсцисс откладываем значения средних напряжений _m, а по оси ординат – значения амплитуд напряжений _а.

Вычислим величины:

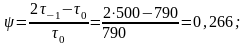
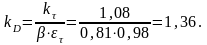
Вычислим значения координат точки В:

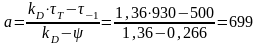МПа;

МПа.

На выбранной системе координат наносим точки:

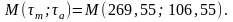
Соединим прямыми точки А с В, В с С, а через точку М из начала координат проведем луч ОMN.

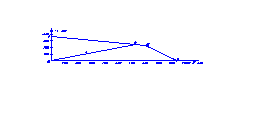
4. При расположении точки N на прямой АВ коэффициент запаса прочности определяем по отношению к усталостному разрушению по формуле:

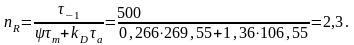
По диаграмме предельных амплитуд коэффициент запаса прочности определяем из соотношения:

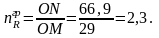
Видим, что коэффициенты совпадают.