
Задача №1
Поперечное сечение бруса состоит из двух частей, соединенных в одно целое.
Требуется:
1. вычертить схему сечения в масштабе 1:2, на которой указать положение всех осей и все размеры;
2. найти общую площадь сечения;
3. определить положение центра тяжести всего сечения;
4. определить осевые и центробежный моменты инерции сечения относительно осей, проходящих через центр тяжести параллельно полкам;
5. Найти положение главных центральных осей, значения главных центральных моментов инерции, главных радиусов инерции и проверить правильность вычисления моментов инерции.

Исходные данные: равнобокий уголок (ГОСТ 8509-93) – 125х125х10; полоса – 250х12.
Решение:
По ГОСТ 8509-93 определим характеристики уголка 125х10:
b = 12,5см; Ауг = 24,33см2;
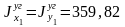 см4;
см4;
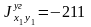 см4;
z0 = 3,45см.
см4;
z0 = 3,45см.
Основные характеристики листа:
h = 25см; t =
1,2см;
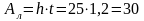 см2;
см2;
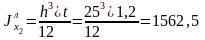 см4;
см4;
 см4.
см4.
1. Изобразим в масштабе 1:2 составное сечение и укажем оси и центры тяжести каждого из элементов.
2. Площадь сечения:
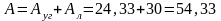 см2.
см2.
3. За исходные координатные оси примем оси х1 и у1 уголка и найдем координаты центра тяжести сечения:
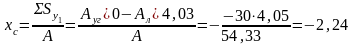 см;
см;
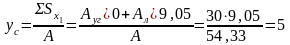 см.
см.
Центральные оси х и у направим параллельно исходным осям х1 и у1.
4. Осевые моменты инерции относительно центральных осей:
 см4;
см4;
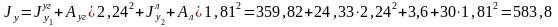 см4;
см4;
Центробежный момент инерции сечения относительно центральных осей:

5. Определим положение главных центральных осей U и V:
 ,
,
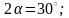
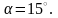
Вычислим значения главных центральных моментов инерции:
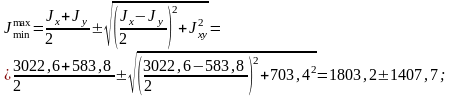
 см4;
см4;
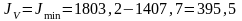 см4.
см4.
Проверка:
 ;
;
 ;
;
 см4,
см4,
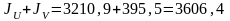 см4,
см4,
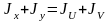 ;
;
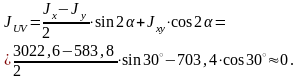
Задача №2
Стальной стержень (Е = 2105МПа), один конец которого жестко защемлен, другой – свободен, находится под действием продольных сил Р и распределенной нагрузки t = 20кН/м. Отдельные участки стержня имеют различную площадь поперечного сечения, F или 2F.
Требуется:
1. сделать схематический чертеж бруса по заданным размерам, соблюдая масштаб длин по вертикали;
2. вычислить значения продольной силы N и нормального напряжения , построить их эпюры;
3. найти перемещение сечения I – I.

Исходные данные: F = 2,9см2; а = 0,19м; b = 0,1м; с = 0,12м; Р = 20кН.
Решение:
Изобразим расчетную схему стержня и разделим ее на три силовых участка.
Определим продольную силу N и нормальное напряжение на каждом участке, начиная со свободного конца.
1-й участок
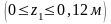
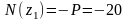 кН;
кН;
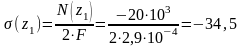 МПа.
МПа.
2-й участок
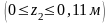
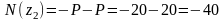 кН;
кН;
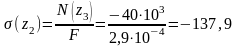 МПа.
МПа.
3-й участок
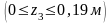
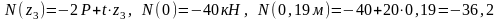 кН;
кН;
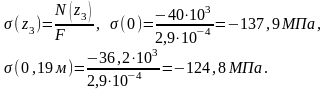
Строим эпюры N и .

Определим перемещение сечения I–I.
Перемещение будет равно удлинению
участка стержня от заделки до нужного
сечения:
Задача №3
Стальной валик прямоугольного сечения испытывает кручение от приложенных к нему четырех моментов: М1, М2, М3 и М4.
Требуется:
1. построить эпюру крутящих моментов;
2. определить размеры поперечного сечения валика из условий прочности и жесткости, приняв h/b = 1,5;
3. показать распределение касательных напряжений в поперечных сечениях;
4. построить эпюру углов закручивания.
Модуль упругости при сдвиге для материала валика G = 8104МПа; допускаемое значение угла закручивания [] = 1,8°/м.

Исходные данные: а = 0,19м; с = 0,1м; l = 0,12м; М1 = 2,9кНм; М2 = 2кНм; М3 = 2,2кНм; М4 = 2,9кНм; [] = 40МПа.
Решение:
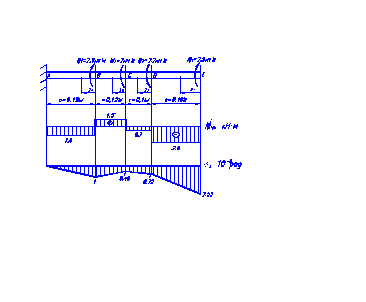
1. Изобразим в масштабе расчетную схему вала.
Строим эпюру
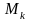 начиная со свободного конца вала.
начиная со свободного конца вала.
1-й участок

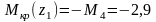 кНм.
кНм.
2-й участок
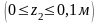
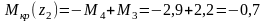 кНм.
кНм.
3-й участок
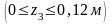
 кНм.
кНм.
4-й участок

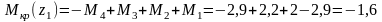 кНм.
кНм.
2. Определяем необходимый диаметр вала.
Из условия прочности:
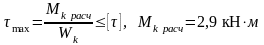 -
с эпюры
-
с эпюры
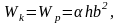 где при h = 1,5b
- = 0,23;
где при h = 1,5b
- = 0,23;
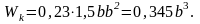
Приравнивая выражение для
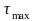 и
и
 получим:
получим:
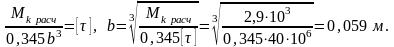
Из условия жесткости:
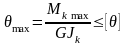 ,
где [] = 1,8°/м =
0,0314м-1;
,
где [] = 1,8°/м =
0,0314м-1;
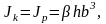 где при h = 1,5b
- = 0,196;
где при h = 1,5b
- = 0,196;
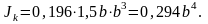
Приравнивая выражение для
 и
и
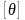 получим:
получим:
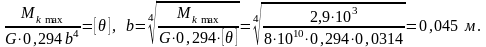
Из двух полученных значений
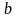 за ответ берем и больший и принимаем из
стандартного ряда
за ответ берем и больший и принимаем из
стандартного ряда
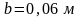 .
.
3. Изобразим распределение касательных напряжений в поперечном сечении вала в точке B.
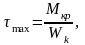
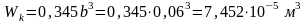 ;
;
 МПа.
МПа.
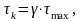 где при h = 1,5b
- = 0,855;
где при h = 1,5b
- = 0,855;
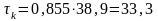 МПа.
МПа.
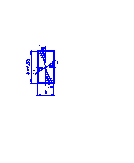
4. Строим эпюру углов закручивания.
Углы поворота сечений будем определять
относительно сечения
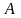 ,
угол поворота которого равен нулю. Углы
поворота других сечений равны сумме
углов закручивания участков вала,
расположенных между сечением
и сечением, угол закручивания которого
определяется:
,
угол поворота которого равен нулю. Углы
поворота других сечений равны сумме
углов закручивания участков вала,
расположенных между сечением
и сечением, угол закручивания которого
определяется:
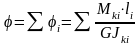 .
.
Т. к. вал имеет одно сечение на всех
участках, вычислим
 .
.
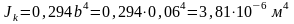 .
.
Угол поворота сечения
 равен углу закручивания участка
равен углу закручивания участка :
:
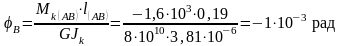 .
.
Угол поворота сечения
 :
:
 .
.
Угол поворота сечения
 :
:
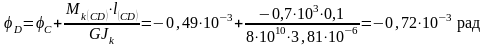 .
.
Угол поворота сечения
 :
:
 .
.
Откладывая от нулевой линии полученные значения углов поворота сечений в масштабе с учетом знака, а затем, соединяя полученные точки прямыми линиями, получаем эпюру углов закручивания.
