
- •1. Определение информации. Семиотика и ее составные части. Фазы обращения информации.
- •2. Структура системы связи. Основные задачи каждого блока системы связи.
- •3. Измерение информации. Дискретный источник информации. Мера информации по Хартли и ее свойство
- •4. Измерение информации по Шеннону.
- •5. Свойства информации по Шеннону.
- •6. Энтропия нескольких источников информации.
- •7. Энтропия непрерывного источника. Относительная энтропия.
- •8. Избыточность источника сообщений.
- •9. Взаимосвязь между энтропией и числом сообщений.
- •10. Пропускная способность двоичного канала.
- •11. Согласование характеристик сигнала и канала.
- •Амплитудная модуляция
- •12. Пропускная способность непрерывного канала с помехами.
- •13. Классификация методов преобразования непрерывной информации в дискретную форму.
- •14. Теорема дискретизации Котельникова в.А. И ее особенности.
- •Свойства ряда Котельникова:
- •15. Корреляционный критерий дискретизации.
- •16. Адаптивные методы дискретизации.
- •Нулевая степень воспроизводящей функции
- •Первая степень приближающего многочлена
- •17. Квантование по уровню. Шум квантования.
- •О терминах
- •Основные принципы построения цап с резистивными цепочками Первый вариант
- •19. Ацп поразрядного взвешивания. Ацп поразрядного уравновешивания на конденсаторах
- •Первый шаг
- •Быстродействие
- •20. Устройство выборки - хранения. Принцип действия и схемы увх
- •21. Распределение мощности в спектре периодического сигнала.
- •22. Спектр периодической последовательности прямоугольных импульсов. Пример.
- •23. Спектр одиночного прямоугольного импульса. Пример.
- •24.Теорема Парсеваля о распределении энергии в спектре непериодического сигнала.
- •25. Взаимосвязь между длительностью импульса и шириной его спектра.
- •26. Спектральная плотность мощности случайного процесса.
- •27. Цели кодирования. Эффективное кодирование. Методы эффективного
- •Цели изучения темы «Эффективное кодирование».
- •Задачи эффективного кодирования.
- •28. Техническая реализация кодирующего и декодирующего устройств эффективного кода.
- •29. Теорема Шеннона о пропускной способности канала без помех и
- •30. Теорема Шеннона о пропускной способности канала при наличии помех. Классификация помехоустойчивых кодов.
- •31. Общие принципы использования избыточности в блоковых кодах.
- •32. Групповой код. Математическое введение. Определение количества
- •33. Таблицы опознавателей и проверочные уравнения для различных кодов (7;4); (7;3); (8;2); (9;3).
- •34. Техническая реализация группового кода и его матричная запись.
- •35. Циклический код. Математическое введение. Выбор образующего многочлена по требуемой корректирующей способности кода.
- •36.Методы построения циклического кода.
- •6.4.1. Методом умножения
- •6.4.2. Методом деления
- •6.4.3. По методу группового кода
- •37. Техническая реализация кодирующих устройств циклического кода по методу умножения (примеры).
- •38. Техническая реализация кодирующих устройств циклического кода по методу деления (примеры).
- •39. Техническая реализация кодирующих устройств циклического кода по методу группового кода (примеры).
- •40. Техническая реализация декодирующих устройств циклического кода, исправляющих одиночную ошибку. Пример.
- •41. Техническая реализация декодирующих устройств циклического кода, исправляющего 2-ые смежные ошибки. Пример.
- •42. Рекуррентный код. Кодирующее и декодирующее устройства. Пример.
- •43.Итеративные коды. Код с повторениями.
- •Модифицированный код с повторением
8. Избыточность источника сообщений.
Из энтропийных оценок источников сообщений, ясно, что она зависит от статических характеристик самих сообщений. Энтропия максимальна при равномерном появлении букв на любом месте сообщения. Для характеристики источника сообщений с различным алфавитом представляет интерес сравнение фактической энтропии источника с максимально возможной. В этом смысле введено понятие избыточности источника сообщений или избыточности алфавита.
 ,
,
где Hmax = log M;
M – количество различных букв в алфавите;
H(X) – средняя энтропия на одну букву.
Избыточность источника R показывает на сколько хорошо используются буквы в данном источнике. Чем меньше R, тем большее количество информации вырабатывается источником на одну букву. Однако, не всегда необходимо стремиться к R = 0. С повышением избыточности повышается помехоустойчивость (надежность) источника. Выяснение количества избыточности важно потому, что мы должны вводить ее разумно, чтобы получить максимальный эффект помехозащищенности, а не полагаться на стихию. Например, избыточность любого языка оказывается порядка 50-70%, то есть если бы все буквы имели одинаковую вероятность использования и можно было бы использовать любые комбинации букв, то среднюю длину слова можно было бы значительно уменьшить. Однако разбираться в этой записи было бы значительно труднее, особенно при наличии ошибок (лектора или студента).
Современные системы связи построены без учета ограничений, существующих в языке, а поэтому не достаточно эффективны, так как они приспособлены для передачи равновероятных букв алфавита, которые могут следовать друг за другом в любых комбинациях.
Колоссальная избыточность присуща телевизионным изображениям: естественно передавать не весь кадр, а только информацию соответствующую тому, чем отличается один кадр от другого. Этим можно существенно сократить требуемую (в среднем) полосу частот.
Различают две составляющие избыточности:
избыточность, обусловленная статистической взаимосвязью букв между собой:
 ,
,
где H(X) – энтропия для букв, когда они неравновероятны и взаимосвязаны;
H1(X) – энтропия для букв, когда они статистически не взаимосвязаны и неравновероятны.
избыточность, обусловленная распределением вероятностей между буквами алфавита:
 .
.
Между R; Rр и Rс существует зависимость: R = Rр + Rс + Rр · Rс.
Если Rр и Rс – невелики, то R ≈ Rр + Rс.
Укрупнение алфавита с M1 элементов алфавита до M2 ≥ M1(M2 = M1n) не изменяет избыточности: R1 = R2.
Но статистические связи между элементами укрупненного алфавита падают Rс ≈ 0; следовательно возрастает неравномерность употребления отдельных букв алфавита M2, то есть Rр2 >> Rр1; Rр2 ≈ R1 ≈ R2.
Доказательство, что R1 ≈ R2 сводится к следующему:
1. Подсчитаем H2(X):
Из свойства аддитивности информации следует, что в одном элементе второго алфавита содержится столько же информации, сколько ее содержится в n элементах первичного алфавита. Среднее количество информации на один элемент первого алфавита – H1; математическое ожидание на n элементов первого алфавита – n · H1 равно информации на один элемент второго алфавита H2(X) = n · H1.
2. Избыточность второго алфавита
 .
.
Избыточность языка подсчитывается по формуле:
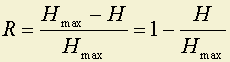 ,
,
где Hmax = log M, а M – число букв в алфавите.
Избыточность языка можно подсчитывать для H0; H1; H2;...HN, где
H∞(X) = 0.87÷1.37бит⁄буква,
а 0; 1; 2… – количество букв между которыми учитываются взаимосвязи.
Примеры.
1. Во сколько раз больше содержится информации на странице текста для иностранца, начавшего изучать новый для себя язык (например, русский) и для носителя языка?
Ответ. Для носителя языка среднее количество информации на одну букву определяется как Hязыка ≈ H30 = 1.35бит⁄буква, а для иностранца, плохо знающего словарь и не учитывающему взаимосвязь букв между собой H = H0 или H1, что соответствует
 ,
,
а
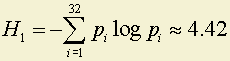 бит⁄буква.
бит⁄буква.
То есть на странице текста для носителя языка содержится информации в

раза меньше информации, чем для иностранца. Частичное знание словаря и закономерностей языка уменьшает эту разницу.
2. Во сколько раз удлиняется текст в деловых бумагах, если их избыточность составляет 90÷95%?
Ответ. При такой избыточности энтропия на одну букву составляет:
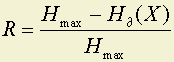 ;
;

;
H¶(X) = 0.25÷0.5бит⁄буква.
В то время как в письменной речи: H∞(X) = 0.87÷1.37бит⁄буква.
Текст удлиняется
в
 раз.
раз.
