6. Энтропия нескольких источников информации.

Пусть имеются два источника XиY, которые выдают события {x₁;x₂;...x_i;...x_n} и {y₁;y₂;...y_j;...y_m}. Рассмотрим одновременное наступление двух событийx_iиx_j. Вероятность его появления обозначимp(x_i;y_j), а вероятности появления любых пар (x_i;y_j) составят матрицу ||p(x_i;y_j)||, где 1 ≤i≤n, а 1 ≤j≤m.

Количество информации, которое будет получено от факта наступления события (x_i;y_j) будет равноI= –logp(x_i;y_j).

Среднее количество информации на одну пару, или энтропия объединения двух событий подсчитывается по формуле:

Для независимых случайных событий XиYвероятность совместного наступления объединения двух событийx_iиy_jопределяется как произведение вероятностей появления каждого из этих событий, то естьp(x_i;y_j) =p(x_i) ·p(y_j). Учитывая это энтропию объединения можно подсчитать по следующей формуле:

то есть энтропия объединения двух независимых источников XиYравна сумме энтропий этих источников. То же можно утверждать об энтропии объединения многих независимых случайных источников, то есть

.

Вероятность совместного наступления объединения двух взаимозависимых событий p(x_i;y_j) подсчитывается как произведение вероятности появления одного из них на условную вероятность появления второго при условии, что имеет место факт появления первого события, то есть

.

Учитывая это, энтропию объединения двух взаимозависимых источников следует считать по иному:

Где 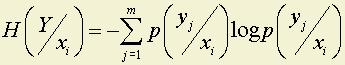– условная энтропия источникаYотносительно событияx_i;

H(^Y⁄_X) – условная энтропия источникаYотносительно источникаX, так как при расчете учитываются все состояния, которые может принимать источникX.

Для объединения из трех взаимозависимых источников X;Y;Zможно записать:

H(X;Y;Z) =H(X) +H(^Y⁄_X) +H(^Z⁄_X;Y).

Для объединения двух взаимозависимых событий можно записать пределы, в которых может меняться его энтропия:

max[H(X);H(Y)] ≤H(X;Y) ≤H(X) +H(Y), то есть

энтропия объединения всегда больше энтропии одного из источников, но меньше суммы их энтропий. Первое утверждение верно, когда имеет место линейная зависимость одного из источников от другого, а второе – когда источники независимы.

Рассмотрим пример расчета энтропии объединения двух источников. Пусть нам задана матрица ||p(x_i;y_j)|| следующего вида:

На матрицу наложены следующие ограничения:

.

Требуется определить H(X;Y) тремя способами:

Надо определить источники XиYвзаимозависимы или нет.

Матрицу ||p(x_i;y_j)|| можно задать самим при условии, что m и n не более четырех, а можно запросить у ЭВМ, которая ее (матрицу) сгенерирует.

При расчетах следует учитывать, что

;

7. Энтропия непрерывного источника. Относительная энтропия.

При попытке оценить неопределенность непрерывной случайной величины (с непрерывным множеством возможных состояний) – появляются особенности.

1. «Непрерывность» имеет смысл только для количеств, то есть объект с непрерывным множеством возможных состояний – это количественная случайная величина.

2. Распределение вероятности по состояниям характеризуется в этом случае плотностью вероятности p(x). Плотность вероятности величина размерная. Размерность обратная размерности случайной величины X, так как вероятность p(x)·dx безразмерна.

Переход к безразмерной случайной величине X, проведем путем деления размерной случайной величины X* на единицу ее измерения X₀. Тогда и плотность вероятности будет безразмерной. Разобьем всю область (–Ґ; +Ґ) возможных значений случайной величины X на интервалы, разделенные отстоящими на равных расстояниях Δx друг от друга интервалами (x_-1; x₀;...x_k;...).

Всякий раз, когда реализуется значение x О (x_k; x_k + Δx) будем считать, что реализовалось значение x_k величины X.

Рис. 2.3

Таким образом перешли к дискретной случайной величине, которая характеризуется распределением вероятностей. Вероятность наступления какого-либо состояния равна

.

Очевидно, что при Δx ® 0 квантованная величина X_д будет все более и более полно отражать все свойства непрерывной величины X. С другой стороны, к величине X_д (дискретной) можно применить понятие энтропии

.

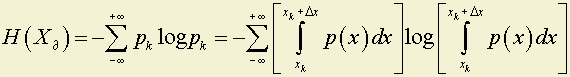Устремим Δx ® 0. При достаточно малых Δx примем . Поэтому

Таким образом предел энтропии H(X_д) за счет второго члена (–log Δx) стремится к бесконечности при Δx ® 0. Убедившись в том, что непрерывные случайные величины не допускают введения конечной абсолютной меры неопределенности, введем относительную меру. В качестве стандарта для сравнения можно брать неопределенность какого-либо простого распределения, например – равномерного в интервале шириной e. Разделим интервал e также на участки Δx и подсчитаем

.

Будем характеризовать неопределенность непрерывной случайной величины X числом, к которому стремится разность энтропий квантованных величин X_д (случайной величины X любого распределения) и X_д;равн(случайной величины, распределенной по равномерному закону на интервале e):

.

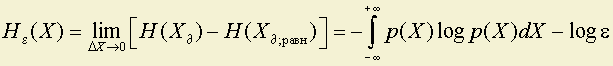Эта разность конечна.

Если взять за стандарт неопределенность случайной величины, равномерно распределенной в единичном интервале, то есть принять (e = 1), то

.

Число H_e=1(X) обычно и называют относительной энтропией непрерывной случайной величины. По численному значению относительной энтропии различные источники сообщения можно сравнить между собой.

Относительная энтропия характеризуется теми же свойствами, что и энтропия дискретного источника:

1. Не зависит от конкретного содержания случайной величины.

2. Энтропия объединения двух независимых источников выражается формулой:

.

3. Энтропия объединения двух статистически зависимых источников:

,

где

.

4. H_e(X; Y) ≤ H_e(X) + H_e(Y).

5. Всякое сглаживание функций распределения p(X) ведет к росту H_e(X).

Рис. 2.4

H_ε1(X) < H_ε2(X).

Исключение составляет лишь то, что H_e(X) может принимать отрицательные значения, так как H_e(X) – это разность энтропий, а случайная величина X может быть распределена на небольшом интервале меньшем, чем (e = 1).

Примеры.

Подсчитайте относительную энтропию непрерывного источника, имеющего следующий закон распределения плотности вероятности случайной величины X:

1.

Рис. 2.5

H_e(x) = 0.

2.

Рис. 2.6

H_e(x) = –1;

.

3.

Рис. 2.7

H_e(x) = 1;

.