40. Техническая реализация декодирующих устройств циклического кода, исправляющих одиночную ошибку. Пример.

Нарисуем общую схему декодирующего устройства с двумя схемами деления.

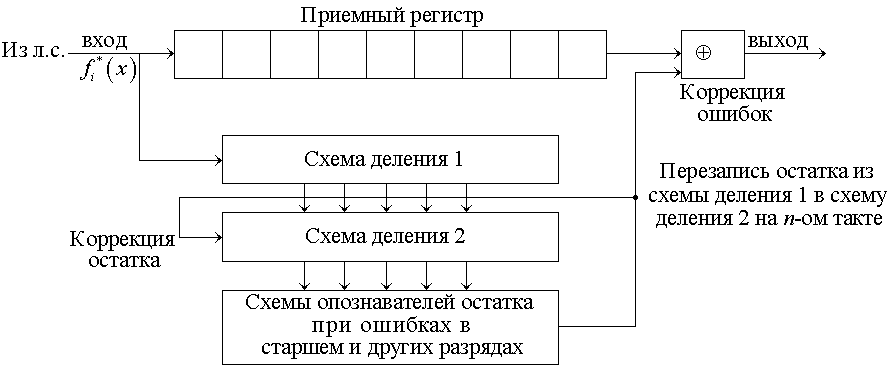
Рис. 6.10. Схема декодирующего устройства с двумя схемами деления

Пусть имеет место ошибка в старшем разряде К.К., принятой из линии связи. Пока она доберется до выхода из приемного регистра, все n тактов она делится в схеме деления 1. На n-ном такте остаток переписывается в схему деления 2. На (n + 1) такте ошибка выходит из регистра и поступает на сумматор. Одновременно из схемы деления 2 кодовая комбинация, соответствующая ошибке в старшем разряде, поступает на схему опознавателя остатка ошибки в старшем разряде. Последняя вырабатывает сигнал на исправление ошибки и обнуление схемы деления 2, если других ошибок нет. Если же ошибка имеет место не в старшем разряде, то остаток, переписанный из схемы деления 1 в схему деления 2, продолжает делиться до тех пор, пока ошибка не доберется до выхода из регистра, то есть в обеих схемах деления 1 и 2 ошибка будет всегда делиться n раз.

Разберем конкретный пример.

Имеем: a_i(x) = x³ Е 1 = 1001; g(x) = x³ Е x² Е 1 = 1101.

Циклический код (7; 4), исправляющий одиночные ошибки.

ƒ_i(x) - послали в линию связи. Из линии связи получили ƒ_i^*(x): 1101011. Необходимо построить схему Д.У., исправляющего одиночные ошибки.

Решение.

1. Выберем схему деления. Пусть это будет схема деления с первого такта.

Рис. 6.11

2. Определим остаток, который получается в схеме деления на n-ном такте ( в нашем случае n = 7), если имеет место ошибка в старшем разряде, то есть . Для этого поделимнаg(x):

Остаток на седьмом такте деления r₇(x) = 100.

3. Спроектируем схему распознавания остатка. Минимальные затраты оборудования (считаются по числу входов-выходов) будут иметь место при инверсии «1» в «0» и установки схемы «исключающего или», когда при входе трех нулей на выходе берется инверсный выход, дающий «1», т.е.

Рис. 6.12

Для построения логических схем можно использовать схемы «И» с прямым и инверсным выходами и схемы «ИЛИ» с прямым и инверсным выходами.

4. Нарисуем схему декодирующего устройства с заведением обратной связи от сигнала коррекции ошибки на обнуление схемы деления 2.

Рис. 6.13

5. Приведем таблицу потактовой работы декодирующего устройства.

Таблица 6.6

№/№ тактов	Вход	Ячейки			Выход	Примечание 1	Примечание 2
		x0	x1	x2
1	1	1	0	1	–	Идет заполнение приемного регистра и деление ƒi*(x) на g(x) в схеме деления 1
2	1	0	1	0	–
3	0	0	0	1	–
4	1	0	0	0	–
5	0	0	0	0	–
6	1	1	0	1	–
7	1	0	1	0	–		Переписывается r(x) в схему деления 2
8	1	0	0	1	1	Соответствует r7(x)	Входной сигнал из регистра начинает поступать на выход
9	–	0	0	0	1 Е 1 = 0	Идет сигнал коррекции
10	–	0	0	0	0	Исправление шестого символа и сброс схемы деления 2 в ноль
11	–	0	0	0	1
12	–	0	0	0	0
13	–	0	0	0	1
14	–	0	0	0	1

На 9-том такте на первый сумматор в схеме деления 2 приходят две единицы: одна от обратной связи с x² и вторая со схемы коррекции. Они дают «0» и все содержание схемы деления 2 превращается в «0». Однако, это не всегда так получается. Особенно, когда n ≠ 2^m – 1 и обращение схемы деления 2 в «0» следует проектировать особо.