29. Теорема Шеннона о пропускной способности канала без помех и

следствие из нее. Способы сжатия информации.

В любом реальном сигнале всегда присутствуют помехи. Однако, если их уровень настолько мал, что вероятность искажения практически равна нулю, можно условно считать, что все сигналы передаются неискаженными. В этом случае среднее количество информации, переносимое одним символом, можно считать:

J(Z; Y) = H_апр(Z) – H_апост(Z) = H_апр(Y),

так как H(Y) = H(Z) и H(Y/Z) = 0, а max{J(Z; Y)} = H_max(Y) – max энтропия источника сигнала, получающаяся при равномерном распределении вероятностей символов алфавита Y.

p( y₁) = p( y₂) = ... = p( y_m) = 1/M_y,

т.е. H_max(Y) = log_aM_y

и, следовательно, пропускная способность дискретного канала без помех в единицах информации за единицу времени равна:

C_y = V_y · max{J(Z; Y)} = V_y · H_max(Y) = V_y · log_aM_y

или C_k = V_k · log_aM_y,

где M_k – должно быть max возможное количество уровней, допустимое для передачи по данному каналу (конечно, M_k = M_y);

V_k – определяется частотными переключательными способностями канала:

Если источник информации создает поток информации

,

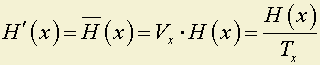а канал связи обладает пропускной способностью С ед. информации в единицу времени, то при H(x) ≤ C:

1. Сообщения, вырабатываемые источником, всегда можно закодировать так, чтобы скорость их передачи была сколь угодно близкой к .

2. Не существует способа кодирования, позволяющего сделать эту скорость большей, чем V_{x max}.

Согласно сформулированной теореме существует метод кодирования, позволяющий при:

H(x) ≤ C – передавать всю информацию, вырабатываемую источником при ограниченном объеме буфера;

H(x) > C – такого метода кодирования не существует, так как требуется буфер, объем которого определяется превышением производительности источника над пропускной способностью канала, умноженной на время передачи.

Из этой теоремы вытекает следующее следствие: если источник информации имеет энтропию H(X), то сообщения всегда можно закодировать так, чтобы средняя длина кода l_ср (количество символов сигнала на одну букву сообщения) была сколь угодно близкой к величине:

,

то есть при а = 2 (бит) и M_y = 2 {0; 1} имеем:

,

где p_i – вероятность встречи данного элемента алфавита;

l_i – количество символов в i-ой кодовой комбинации;

ε – бесконечно малая величина ≥ 0, т.е. lim l_ср = H(x).

Это следует из равенства:

.

Таким образом, l_ср выступает критерием эффективности кодирования. Чем ближе l_ср к H(x), тем лучше мы закодировали. В инженерной практике это различие можно считать допустимым 3÷5% (до 10%). Из этого же критерия следует, что если буквы имеют равномерное распределение вероятностей их употребления, то

H(x) @ log₂ M,

а l_ср тоже равно log₂ M. Пределы эффективного кодирования:

H(x) ≤ l_ср ≤ log₂ M.

30. Теорема Шеннона о пропускной способности канала при наличии помех. Классификация помехоустойчивых кодов.

Теория помехоустойчивого кодирования базируется на результатах исследований, проведенных Шенноном и сформулированных им в виде теоремы:

• при любой производительности источника сообщений, меньшей, чем пропускная способность канала, существует такой способ кодирования, который позволяет обеспечить передачу всей информации, создаваемой источником сообщений, со сколь угодно малой вероятностью ошибки;

• не существует способа кодирования, позволяющего вести передачу информации со сколь угодно малой вероятностью ошибки, если производительность источника сообщений больше пропускной способности канала.

Хотя доказательство этой теоремы, предложенной Шенноном, в дальнейшем подвергалось более глубокому и строгому математическому представлению, идея его осталась неизменной. Доказывается только существование искомого способа кодирования, для чего находят среднюю вероятность ошибки по всем возможным способам кодирования и показывают, что она может быть сделана сколь угодно малой. При этом существует хотя бы один способ кодирования, для которого вероятность ошибки меньше средней.

Источник создает информацию со скоростью V_х букв в секунду и энтропией каждой буквы в среднем Н(х), т.е. его производительность:

Н(х) = V_х · Н(х) [бит/сек].

В соответствии с теоремой о эффективном кодировании среднее количество символов на одну букву l_ср ≥ Н(х), т.е. в первом приближении можно получить, что

Н(х) = V_х · l_ср [бит/сек].

Условие пропуска информации по каналу Н(х) ≤ C = V_k.

При наличии помех пропускная способность канала связи падает, т.е. при двоичном симметричном канале имеем:

C_k = V_k · [1 – H(P_ош)].

Теорема о помехоустойчивом кодировании требует чтобы

V_x · l_ср = Н(х) ≤ C_k = V_k · [1 – H(P_ош)].

где l_ср – средняя длина кодовой комбинации для записи одной буквы.

По сравнению с эффективным кодом l_ср увеличивается до:

.

Однако, такой величины l_ср1 помехоустойчивые коды не достигают. Это можно рассматривать как теоретический предел.

Обеспечение передачи информации с весьма малой вероятностью ошибки и достаточно высокой эффективностью возможно при кодировании чрезвычайно длинных последовательностей знаков. На практике степень достоверности и эффективности ограничивается двумя факторами: размерами и стоимостью аппаратуры кодирования и декодирования и временем задержки передаваемого сообщения. В настоящее время используются относительно простые методы кодирования, которые не реализуют возможностей, указанных теорией. Однако постоянно растущие требования в отношении достоверности передачи и успехи в технологии создания больших интегральных схем способствуют внедрению для указанных целей все более сложного оборудования.

Классификация кодов:

В этом случае кодирование должно осуществляться так, чтобы сигнал, соответствующий принятой последовательности символов, после воздействия на него предполагаемой в канале помехи оставался ближе к сигналу, соответствующему конкретной переданной последовательности символов, чем к сигналам, соответствующим другим возможным последовательностям. (Степень близости обычно определяется по числу разрядов, в которых последовательности отличаются друг от друга.)

Это достигается ценой введения при кодировании избыточности, которая позволяет так выбрать передаваемые последовательности символов, чтобы они удовлетворяли дополнительным условиям, проверка которых на приемной стороне дает возможность обнаружить и исправить ошибки.

Коды, обладающие таким свойством, называют помехоустойчивыми. Они используются как для исправления ошибок (корректирующие коды), так и для их обнаружения.

У подавляющего большинства существующих в настоящее время помехоустойчивых кодов указанные условия являются следствием их алгебраической структуры. В связи с этим их называют алгебраическими кодами. (В отличие, например, от кодов Вагнера, корректирующее действие которых базируется на оценке вероятности искажения каждого символа.)

Алгебраические коды можно подразделить на два больших класса: блоковыеинепрерывные.

В случае блоковых кодов процедура кодирования заключается в сопоставлении каждой букве сообщения (или последовательности из kсимволов, соответствующей этой букве) блока изnсимволов. В операциях по преобразованию принимают участие только указанныеkсимволов, и выходная последовательность не зависит от других символов в передаваемом сообщении.

Блоковый код называют равномерным, еслиnостается постоянным для всех букв сообщения.

Неравномерныеблоковые коды не употребляются из-за сложности устройств необходимых для их реализации.

При кодировании разделимымикодами выходные последовательности состоят из символов, роль которых может быть отчетливо разграничена. Это информационные символы, совпадающие с символами последовательности, поступающей на вход кодера канала, и избыточные (проверочные) символы, вводимые в исходную последовательность кодером канала и служащие для обнаружения и исправления ошибок.

При кодировании неразделимымикодами разделить символы выходной последовательности на информационные и проверочные невозможно.

Непрерывными(рекуррентными) называют такие коды, в которых введение избыточных символов в кодируемую последовательность информационных символов осуществляется непрерывно, без разделения ее на независимые блоки. Непрерывные коды также могут быть разделимыми и неразделимыми.