26. Спектральная плотность мощности случайного процесса.

Мы научились представлять на спектральной оси:

• периодические сигналы;

• непериодические, но ограниченные во времени.

Но не научились представлять:

• непериодические, неограниченные во времени случайные сигналы.

К случайной функции непосредственно применить преобразование Фурье нельзя, поскольку она не определени точно. Однако для любой из реализаций ƒ_ν(t) конечной длительности T можно найти преобразование Фурье F_ν(jω), то есть

,

где – общая энергия ν-той реализации случайной функции ƒ(t);

|F_ν(jω)| – модуль спектральной функции ƒ(t) для ν-той реализации.

Средняя мощность ν-той реализации может быть подсчитана по формуле:

,

где – спектральная плотность ν-той реализации случайной функции ƒ(t).

Если T ® Ґ, то

.

Восстановить реализации процесса как функции времени по энергетическому спектру в принципе нельзя.

Получить N(ω) практически сложно, так как требуется усреднить много реализаций случайной функции ƒ_ν(t).

Для эргодических процессов достаточной является одна достаточно длинная реализация, так как для них среднее по множеству можно заменить средним по времени, то есть:

.

Найдем иную запись для энергетического спектра случайного прочесса

.

Учитывая это, можно записать

.

Если θ и ν – находятся в следующем взаимоотношении: t = θ + τ; dt = dτ, то

где

–

автокорреляционная функция случайного процесса ƒ(t).

По аналогии с преобразованием Фурье:

.

Спектр случайного процесса может быть задан только энергетически:

Рис. 10.20

Для белого шума τ₀ – время корреляции стремится к нулю и корреляционная функция стремится к δ-функции.

.

Рис. 10.21

Таблица 10.1

Вид сигнала	Его спектр – спектр амплитуд	Энергетический спектр – энергия
1. Периодический, бесконечный во времени
	где An – амплитуда гармоник
2. Спектр сигнала непериодического ограниченного во времени
3. Спектр случайного процесса – энергетический

27. Цели кодирования. Эффективное кодирование. Методы эффективного

кодирования. Его недостатки.

Цели изучения темы «Эффективное кодирование».

Целями изучения темы «Эффективное кодирование» являются умения:

1. Вести эффективное кодирование разных дискретных источников, как с независимыми последовательностями букв, так и взаимозависимыми и особенно для источников, которые могут быть описаны разными моделями. Для этого необходимо уметь считать энтропию таких разных источников информации.

2. Усвоить и применять критерий эффективного кодирования.

3. Уметь считать величины выигрышей при применении эффективного кодирования. Для этого необходимо изучить теорию, освоить решение задач, выполнить лабораторную работу и ответить на вопросы коллоквиума.

4. Строить кодирующие и декодирующие устройства.

Задачи эффективного кодирования.

Эффективное кодирование решает задачу более компактной записи сообщений, вырабатываемых источником за счет их перекодировки. И применяется практически во всех архиваторах типа Rar, Zip и др. Особенностью этих архиваторов является то, что они позволяют сжать информацию в относительно небольшое число раз (в 2-3, max в 4 раза), но при этом происходит полное восстановление сжатой информации «бит в бит».

Если же не требуется восстановление информации «бит в бит», то применяются другие методы перекодировки, позволяющие достичь сжатия в десятки раз. Они основываются на изучении закономерностей создания сообщений источником, изучении свойств самого источника и понимания того, насколько необходимо сохранять начальную информацию для потребителя.

Например, при передаче речи можно не передавать ее «бит в бит», а допускать искажения, которые получатель голосового сообщения просто не заметит из-за нечувствительности слухового аппарата человека к этим изменениям. При этом сохранится и разборчивость речи, и узнаваемость голоса, и ее эмоциональная окраска. Частичная потеря этих качеств увеличивает ее сжатие. Еще раз подчеркнем, что эффективное кодирование это сжатие и восстановление информации «бит в бит».

Метод Хафмена

От указанного недостатка свободна методика Хаффмена. Она гарантирует однозначное построение кода с наименьшей для данного распределения вероятностей средним числом символов на букву.

Для двоичного кода методика сводится к следующему. Буквы алфавита выписываются в порядке убывания вероятностей в один столбец. Две последние буквы объединяются в одну вспомогательную букву, которой приписывается суммарная вероятность. Полученные буквы снова выстраиваются в дополнительный столбец, в котором вспомогательная буква из предыдущего столбца в новом столбце ставится в соответствии с ее суммарной вероятностью (в дополнительном столбце вспомогательные буквы подчеркнуты), а две последние буквы снова объединяются в одну. Процесс продолжается до тех пор, пока не получим единственную вспомогательную букву с вероятностью равной 1. По данной методике составим таблицу.

Таблица 3.5

		1	2	3	4	5	6	7	код
Z1	0,22	0,22	0,22	0,26	0,32	0,42	0,58	1	01
Z2	0,20	0,20	0,20	0,22	0,26	0,32	0,42		00
Z3	0,16	0,16	0,16	0,20	0,22	0,26			111
Z4	0,16	0,16	0,16	0,16	0,20				110
Z5	0,10	0,10	0,16	0,16					100
Z6	0,10	0,10	0,10						1011
Z7	0,04	0,06							10101
Z8	0,02								10100

Для составления кодовой комбинации, соответствующей данному сообщению, необходимо проследить путь перехода сообщения по строкам и столбцам таблицы. Для наглядности строится кодовое дерево. Из точки, соответствующей вероятности 1, направляются две ветви, причем ветви с большей вероятностью направляются влево и им приписывается символ 1, с меньшей – 0. Такое последовательное ветвление продолжаем до тех пор, пока не дойдем до вероятности появления каждой буквы.

Рис. 3.2. Кодовое дерево

Теперь, двигаясь по кодовому дереву сверху вниз, можно записать для каждой буквы соответствующую ей кодовую комбинацию:

.

Рассмотрев методики построения эффективных кодов, нетрудно убедиться в том, что эффект достигается благодаря присвоению более коротких кодовых комбинаций более вероятным буквам и более длинных менее вероятным буквам. Таким образом, эффект связан с различием в числе символов кодовой комбинации.

А это приводит к трудности при декодировании.

Метод Шенона:

Код строится следующим образом: буквы алфавита сообщения выписываются в таблицу в порядке убывания вероятностей. Затем они разбиваются на две группы так, чтобы суммы вероятностей в каждой из групп были бы по возможности одинаковы.

Всем буквам верхней половины в качестве первого символа приписывается 0, а всем нижним 1, или наоборот, это не принципиально, но правило должно оставаться до завершения кодирования всех букв.

Каждая из полученных групп в свою очередь разбивается на две подгруппы с одинаковыми суммарными вероятностями и так далее. Процесс повторяется до тех пор, пока в каждой подгруппе останется по одной букве.

Рассмотрим алфавит из восьми букв. Ясно, что при обычном (не учитывающем статистических характеристик) кодировании для представления каждой буквы требуется 3 символа.

Наибольший эффект сжатия получается в случае, когда вероятности букв представляют собой целочисленные отрицательные степени двойки. Среднее число символов на букву в этом случае точно равно энтропии источника.

Убедимся в этом. Рассмотрим алфавит:

Таблица 3.1

Буквы	Вероятность	Кодовые комбинации
Z1	1/2	1	1
Z2	1/4	01	1	2
Z3	1/8	001		2	3
Z4	1/16	0001			3
Z5	1/32	00001
Z6	1/64	000001
Z7	1/128	0000001
Z8	1/128	0000000

Вычислим энтропию алфавита:

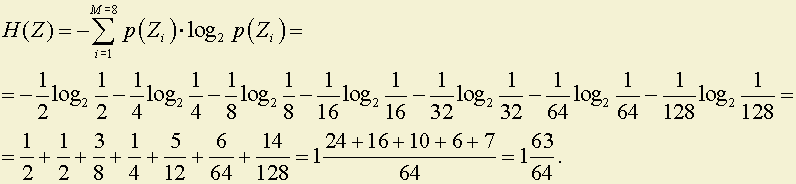
Вычислим среднее число символов на букву по формуле:

.

В более общем случае для алфавита из 8 букв среднее число символов на букву будет меньше 3, но больше энтропии алфавита H(Z).

В общем случае:

H(Z) ≤ l ≤ log₂M,

.