24.Теорема Парсеваля о распределении энергии в спектре непериодического сигнала.
Пусть непериодический сигнал описывается функцией ƒ(t). Тогда энергию, выделяемую сигналом на сопротивлении в 1 ом, можно записать:
.
Предположим, что ƒ(t) абсолютно интегрируема (интеграл сходится). Выразим энергиюWчерез модуль спектральной характеристикиF(ω).
Квадрат модуля спектра амплитуд можно представить в виде:
,
где F(–jω) – комплексно-сопряженная функция от спектральной характеристикиF(jω).
;
.
Согласно определению можно записать:
.
Рассмотрим выражение:
и поменяем очередность интегрирования
.
Однако в соответствии с обратным преобразованием Фурье:
.
Или окончательно:
.
Оказывается, что энергия при интегрировании квадрата временной функции во временном интервале равняется энергии при интегрировании квадрата модуля спектра амплитуд по всему интервалу частот (теорема Парсеваля).
25. Взаимосвязь между длительностью импульса и шириной его спектра.
Понятие о текущем и мгновенном спектрах.
Спектр одиночного импульса имеет следующий вид:
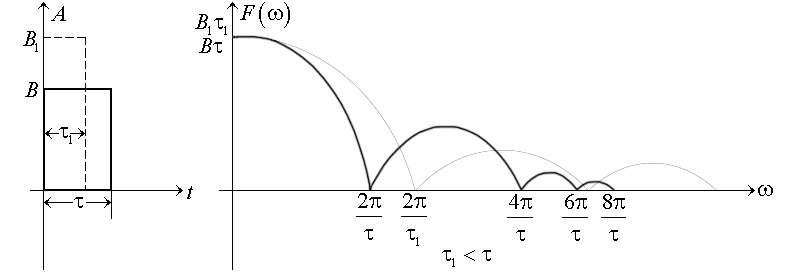
Рис. 10.16. Спектр одиночного импульса
Из спектра одиночного
импульса ясно, что чем меньше
, тем шире спектр. При
® 0 – спектр равномерный;
а при
= Ґ – имеем на спектре
одну постоянную составляющую.
Эта связь вытекает непосредственно из общего свойства преобразования Фурье.
Пусть ƒ(t) соответствует спектрF(ω).
Изменим масштаб функции ƒ(t) по оси времени вaраз и рассмотрим спектр функцииaƒ(at):
,
заменим переменные at=z;adt=dz;t=z/a, то есть длительность функции ƒ(t) уменьшится вaраз, во столько же раз возрастет ширина ее спектра.
Вопрос о соотношении между длительностью импульса и шириной его спектра имеет громадное практическое значение. В вычислительной технике необходимы короткие и мощные импульсы и в тоже время требуется, чтобы спектр импульса был как можно уже, так как широкие спектры вызывают трудности при создании аппаратуры.
Эти требования противоречивы.
Возникает вопрос: нельзя ли найти такие сигналы, которые обладали бы ограниченным спектром и одновременно ограниченной длительностью? Формализм преобразования Фурье этого не позволяет, однако для реальных сигналов могут быть введены разумные ограничения, которые позволяют ограничить либо Δt, либо Δƒ, либо и то и другое.
Наиболее удобным в этом смысле, как мы уже говорили ранее, является энергетический критерий. При этом можно представить себе следующие модели сигналов:
1. Сигналы ограничены во времени. Спектр – неограничен теоретически; физически он всегда ограничен и учитывается только та часть спектра, где сосредоточена подавляющая часть энергии сигнала.
2. Сигналы имеют ограниченный спектр, то есть математически это периодические, неограниченные во времени сигналы. Фактически, реальный процесс всегда ограничен во времени, поэтому учитывается только интервал времени, в котором сосредоточена подавляющая часть всей энергии сигнала.
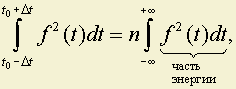
где t0– часто задается естественно: для симметричного импульсаt0= 0; для одиночного так жеt0= 0 и формула имеет вид:
.
3. Сигналы, у которых и длительность (Δt) и ширина спектра (Δƒ) ограничены как интервалы, в которых сосредоточена подавляющая часть энергии сигнала. Математический аппарат преобразования Фурье дает в этом случае приближенные разультаты.
При ограничениях по Δtи Δƒ можно поставить следующую задачу – отыскать такую форму сигнала, для которой произведение Δt· Δƒ достигает min.
Такому условию соответствует импульс, имеющий колоколообразную форму, которая описывается кривой Гаусса(кривой нормального распределения).
Рис. 10.17. Кривая Гаусса
Произведение Δt· Δƒ может быть уменьшено только до определенного предела:
Δt· Δƒ ≈ const > 0,
где const зависит от выбора определения Δƒ и Δt.
Приведем значения Δt· Δƒ для различных видов сигналов в предположении, что
,
где η = 0.9.
Δt· Δƒ – max для импульсов с разрывом (экспонента, прямоугольник); меньше для импульсов с разрывом в первой производной (треугольник и косинусоидальный) и наименьшее значение у колоколообразного импульса, у которого функция непрерывна со всеми своими производными.
Наиболее плодотворной и близкой к реальной действительности является модель с ограниченным спектром.
Этому способствует тот факт, что спектр мощности реального сигнала достаточно быстро спадает вне интервала частот, на который приходится основная часть мощности.
В инженерной практике принимают (в первом приближении независимо от формы сигнала):
Δt· Δƒ ≈ 1.
Практически, независимо от формы сигнала содержится > 90% энергии.
Примеры.
1. Если Tимп= 3млсек, то какая требуется полоса частот, чтобы пропустить основную долю энергии?
.
2. Какова длительность телевизионных импульсов, если FTVmax= 6мггц?
.
3. Какова min длительность импульсов, проходящих по телефонному каналу?
4. При передаче трансцоидального импульса происходит его искажение. Чаще всего это сглаживание (показано пунктиром). На рис. 10.18. показаны длительность импульса и длительности фронтов (переднего и заднего). Из приведенных соотношений видно, что для сохранения фронтов требуется значительно более широкий спектр, чем для передачи основной энергии импульса.
Рис. 10.18
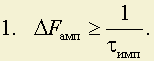
Если сохранить фронт, то:
так как
,
то ΔFф>> ΔFимп.
Реальный физический процесс не может быть в точности предсказан, так как сведения о нем мы получаем в результате наблюдений. Мы не можем выполнить интегрирование в бесконечных пределах, а только до настоящего,текущегомомента. Прошлое же нам может быть известно (в принципе). Поэтому нарядусо спектром, в котором полагали функцию ƒ(t) не ограниченной по времени, т.е.
используется характеристика
,
которая называется текущим спектром.
Очевидно, имеет смысл понятие о спектре, изменяющемся во времени, и отражающем свойства процесса в данный момент.
Простейшее определение мгновенного спектра
,
то есть мгновенный спектр определен как спектр процесса длительностью T, непосредственно предшествующего данному моментуt, то есть мы имеем дело со скользящим интегрированием: интервал интегрирования имеет постоянную длину, но перемещается по оси времени.
Более общее определение мгновенного спектра состоит в том, что в подинтегральное выражение вводится скользящая, то есть связанная со временем весовая функция.
Определение принимает вид:
.