21. Распределение мощности в спектре периодического сигнала.

Средняя мощность периодического сигнала может быть представлена в циклах периода:

и ƒ(t) может быть представлена так:

.

Если подставить ƒ(t) в P_ср, то получим

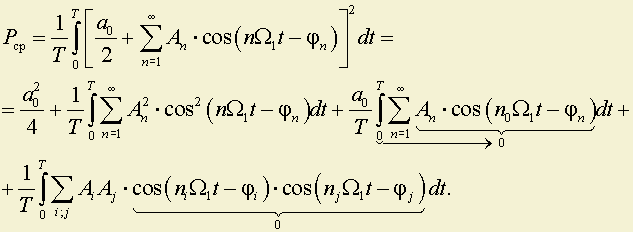
1. Квадраты входят в .

2. Интеграл за период от произведения косинусоид кратных частот равен 0.

3. 

;

;

.

Таким образом, средняя мощность, выделяемая сложным периодическим сигналом в активном сопротивлении, равна сумме средних мощностей, выделяемых в этом сопротивлении отдельными гармониками тока и его постоянной составляющей.

Средняя мощность не зависит от фаз гармоник.

Это означает, что изменение формы сигнала, получающееся при нарушении фазовых соотношений внутри спектра, не связано с изменением средней мощности сигнала, то есть для определения средней мощности начало отсчета не играет роли.

22. Спектр периодической последовательности прямоугольных импульсов. Пример.

Реальные устройства систем связи и управления содержат инерционные элементы (индуктивности, емкости). Поэтому невозможно передавать по такой системе гармонические составляющие сколь-угодно больших и малых частот.

Очевидно, что передавать следует гармонические составляющие с относительно большими амплитудами, содержащими большую долю энергии.

Поэтому вводится понятие практической ширины спектра сигнала.

К нему можно подходить с 2-х точек зрения:

1. Сохранить основную энергию сигнала, т.е. учитывать ширину спектра, в которой сосредоточена подавляющая часть энергии сигнала.

Рис. 10.3

2. Сохранить не только энергию, но и форму сигнала. Это требование резко расширяет требуемую полосу частот.

Пример

Найти спектр периодической последовательности прямоугольных импульсов.

Рис. 10.4

Дано:

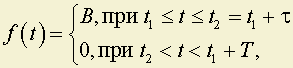
где t₁– любой момент времени относительно некоторого начала отсчетаt= 0.

Можно записать:

то есть

Амплитуда гармоники:

Постоянная составляющая .

При n® ҐA_n® 0;A_n– промодулированы 1/nубывающими синусоидами, то есть убывание довольно резкое (доN-ой гармоники).

Положим для определенности =T/4, тогда

;

.

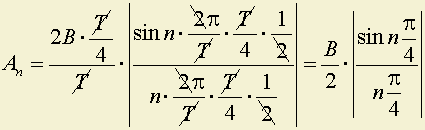1. Постоянная составляющая

2.

3.

4.

5.

6.

7.

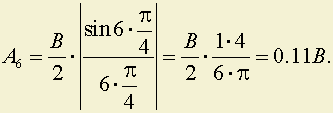
8.

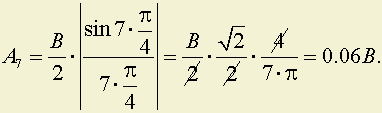
9. и т.д.

Рис. 10.5

Огибающая этого спектра определяется:

где Ω = n· Ω₁.

Фазы гармоник Ψ – зависят от выбора начала отсчета во времени – t₁.

Частоты нулевых амплитуд:

;

;

.

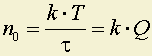При ,Q= 4,

,

то есть 4Ω₁; 8Ω₁; 12Ω₁... .

Определим практическую ширину спектра для сигнала.

–скважность, Q= 2.

Рис. 10.6

Примем за практическую ширину спектра сумму гармоник, которые несут > 0.9 энергии сигнала.

;

;

;

; ;,

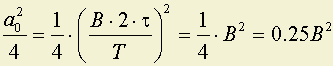то есть практически можно ограничиться спектром в 2÷3Ω₁, так как вклад остальных гармоник невелик.

Что произойдет со спектром, если Q® Ґ,, то есть® 0? Определим качественно каков спектр периодической последовательности очень узких импульсов.

1. Соседние спектральные составляющие появляются через интервал .

2. Энергия одной составляющей падает:

так как ® 0.

3. Положение первого нуля отодвигается в бесконечность:

;

.

23. Спектр одиночного прямоугольного импульса. Пример.

Рис. 10.8

Модуль функции F(jω) равен:

.

;

периоды нулей ® ;

.

Рис. 10.9

Отсюда спектр одиночной импульсной δ-функции Дирака находится из предыдущего, если:

B= 1/при® 0, то

;

.

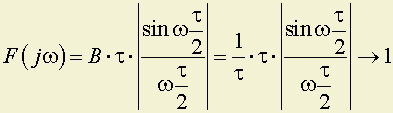Рис. 10.10

Рассмотренные ранее спектры относятся к функциям, ограниченным во времени, т.к. для них требуется выполнение условия:

.

Пример.