16. Адаптивные методы дискретизации.

На каждом интервале дискретизации находится некоторая функцияy_j(t) выбранного типа в предположении, что она наилучшим образом (в смысле выбранного показателя качества) будет отображать функцию x(t) на этом интервале .

Указанное условие проверяется и, если необходимо и возможно, то находится новая функция, наилучшим образом воспроизводящая функцию x(t).

На интервале регистрируются отсчёты значений функцииx_j(t) или некоторые характеристики функции y_j(t) – например, коэффициенты разложения, по которым можно восстановить исходную функцию с погрешностью, не превышающей допустимую.

Рассмотрим в качестве воспроизводящих функций функции нулевой и первой степеней.

Нулевая степень воспроизводящей функции

Воспроизводящая функция y(t) на отрезке выбирается следующим образом:

Рис. 9.15

• y(t_i) = x(t_i);

• вычисляем разность Δ = x(t) – y(t_i) = x(t) – x(t_i);

• сравниваем Δ с ε;

• t_{i + 1} – момент времени, когда |Δ| = ε;

• y(t_{i + 1}) = x(t_{i + 1}) и т.д.

Первая степень приближающего многочлена

а) Экстраполяционный метод

|x(t) – (ƒ(t_i) + ƒ'(t_i)Δt_i)| ≤ ε на отрезке [t_i, t_{i + 1}].

Рис. 9.16

б) Интерполяционный метод (обладает большой помехоустойчивостью)

Δ = |x(t) – kΔt_i| ≤ ε₀.

Рис. 9.17

В зависимости от результата сравнения принимается решение либо о дальнейшем увеличении отрезка [t_i, t_{i + 1}], либо о формировании выборки сигнала x(t_i).

Для выполнения этой дискретизации необходимо:

• хранить сигнал ƒ(t) на отрезке [t_i, t_{i + 1}];

• проводить значительный объем вычислительных операций (аппаратно или программно).

Реализация способа более сложная, чем экстраполяционного, но число отсчетов существенно сокращается.

Ещё больше сокращается число отсчетов, если принять в качестве воспроизводящей функции полиномы Чебышева или Лежандра второй степени.

17. Квантование по уровню. Шум квантования.

ринцип квантования по амплитуде заключается в том, что вводятся фиксированные уровни сигнала и все значения функции ƒ(t), находящейся между введенными фиксированными уровнями, относятся к одному из них.

Весь вопрос заключается в выборе величины одного кванта сигнала.

Величина кванта выбирается из практических соображений. Практически мы никогда не можем измерить точно значение функции в какой-нибудь момент времени из-за наличия неизбежных помех и искажений.

Рассмотрим некоторые виды искажений.

Рис. 9.8

1. Дрейф нуля во времени.

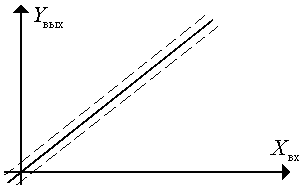
Рис. 9.9

Смещение функции X_вых = Y(X_вх).

2. Изменение Кус со временем.

Рис. 9.10

3. Нелинейность преобразования.

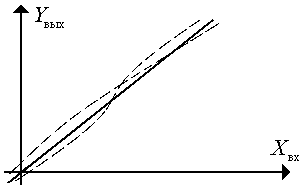
Рис. 9.11

Если эти искажения могут быть каким-либо образом предсказаны и следовательно тем или иным способом скомпенсированы, то влияние случайной помехи предсказать нельзя.

Естественно нет смысла передавать точно измеренное значение, если не известно, что измерено: сама передаваемая величина или она не изменилась, а на нее наложилась помеха.

Рис. 9.12

Y_вых = Y(X_вх) + ξ – аддитивная помеха;

Y_вых = Y(X_вх) · ξ – мультипликативная помеха.

Если мы хотим быть уверены в том, что передается новое значение, т.е. величина x(t) действительно изменилась, то мы должны выбирать дискретную шкалу так, чтобы помеха не превосходила половины интервала между соседними уровнями.

При этом, приняв сигнал некоторой величины мы относим его к ближайшему дискретному значению.

Механизм квантования на передающем конце сводится к тому, что вместо данного мгновенного значения передаваемой величины (при непрерывном сообщении) передается ближайшее дискретное значение. Ближайшие сообщения отличаются на величину Δx, которую называют шагом квантования.

Таблица 9.1

n · Δt	1	2	3	4	5	6	7	8	9
n · Δx	1	2	3	3	3	3	3	4	6

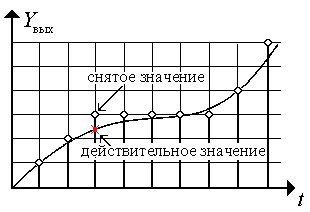
Рис. 9.13

Ясно, что квантование сопровождается искажением, т.к. полученные импульсы воспроизводят сигнал не точно.

Разность между квантованными импульсами и импульсами функции ƒ(k · Δt) высотой в n(k · Δt) · Δy образует последовательность импульсов

ξ(k · Δt) = ƒ(k · Δt) – n(k · Δt) · Δy,

которая называется шумом квантования.

18 . ЦАП.