14. Теорема дискретизации Котельникова в.А. И ее особенности.

В качестве достаточно универсальной модели сигнала принимается случайный процесс.

Пусть каждая из реализаций этого случайного процесса представляет функцию с ограниченным спектром ω ≤ ω_max= 2πƒ_max.

В этом случае для преобразования непрерывного сигнала в дискретно-непрерывный можно использовать теорему Котельникова.

В 1933 году Котельникова В.А. доказал, что сигнал, описываемый функцией с ограниченным спектром, полностью определяется дискретным рядом значений, отсчитанных через максимально допустимые интервалы времени

,

где ƒ_max– максимальная частота в спектре сигнала.

Следовательно, если требуется передать сигнал, описываемый дискретной функцией ƒ(t) с ограниченным спектром, то достаточно передавать отдельные мгновенные значения, отсчитанные через конечный промежуток времени. По этим значениям непрерывный сигнал может быть полностью восстановлен на выходе системы:.

Это положение объясняется тем, что отсутствие высших гармоник в составе ƒ(t) накладывает ограничения на способы, которыми могут быть соединены каждые две соседние точки.

Рис. 9.3

Доказательство состоит в разложении функции ƒ(t) в особого рода ряд.

В общем случае

,

где

.

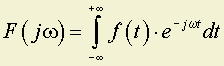В данном, частном случае имеем

.

В момент времени

;

Функция же F(jω) на конечном промежутке (–ω_m; ω_m) может быть разложена в ряд Фурье по частотам следующим образом (путём её периодического продолжения с периодом 2ω_mна весь интервал частот ω от –∞ до ∞)

;

;

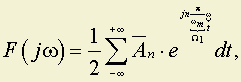
где

;

Рис. 9.4

Из сравнения (9.1) и (9.2) следует

.

Таким образом коэффициенты A_nпропорциональны значениям функции ƒ(t) в дискретные момента времени.

Коэффициенты A_nполностью определяютF(jω), а последняя полностью определяет функцию ƒ(t).Следовательно, знание значений функции ƒ(t) в моменты времени достаточно для полного определения функции ƒ(t).

Рассмотрим теперь восстановление функции ƒ(t) по её значениям в моменты времениt_n.

F(jω) – периодическая;

ƒ(t) – в пределах 1-го периода.

если заменить на f(nΔt), то изменится знак вe^–jnΔtω

Восстановление идет по функции.

1. f(nΔt) – значенияf(t) в моменты времениnΔt.

2. – функция, принимающая max = 1 в точкеt=nΔt, а в остальных точкахkΔt, гдеk≠nравна нулю, так какt=kΔt, то

.

Рассмотрим смысл этого выражения.

Рис. 9.5

Свойства ряда Котельникова:

1. Каждое слагаемое превращается в нуль при всех значениях, при которых (уже показали).

2. Для восстановления истинного значения функции в любой момент времени, кроме точек отсчета, нужно вычислять бесконечную сумму ряда. Это существенный недостаток теоремы Котельникова.

3. Теорема Котельникова применима лишь для сигналов с ограниченным спектром, т.е. принципиально для сигналов бесконечных во времени.

Несмотря на указанные недостатки, теорема Котельникова широко используется на практике при наличии ограничений на спектр сигнала.

15. Корреляционный критерий дискретизации.

Отличительные свойства непрерывного сигнала в модели Железнова Н.А. следующие:

• спектр сигнала сплошной и отличен от нуля на всей оси частот;

• сигнал имеет конечную длительность;

• рассматриваемые сигналы могут быть представлены как стационарными, так и нестационарными случайными функциями;

• функция корреляции равна нулю вне интервала корреляции .

Длительность сигнала Т должна быть во много раз больше :

Т >> .

Неограниченность спектра и конечная длительность сигнала являются большими преимуществами этой модели: она в большей степени соответствует свойствам реальных сигналов, чем модель В.А. Котельникова.

Единственным ограничением в этой модели является ограничение функции корреляции, которая имеет вид, показанный на рисунке.

Рис. 9.6

Это означает, что соседние значения функции отсчитанные через промежуток времени больший, чем , могут считаться независимыми.

.

Для стационарных случайных сигналов, обладающих перечисленными выше свойствами Н.А. Железновым было показано, что они могут быть представлены системой линейного прогнозирования со среднеквадратичной ошибкой , как угодно мало отличающейся от нуля, лишь в промежутке времени, равном интервалу корреляции.

Таким образом, для непрерывного сигнала конечной длительности Т (при условии, что T >> ) число некоррелированных отчётов не превышает величиныN.

.

Следовательно, дискретизация непрерывной функции с интервалом обеспечивает возможность безошибочного восстановления значений непрерывной функции внутри интерваловс помощью системы линейного прогнозирования.

Интервал корреляции для реальных сигналов определяется следующим образом.

Вводится понятие эффективной полосы частот сигнала

,

где N_Xmax – максимальное значение спектральной плотности мощности сигнала.

,

а

.

Δω_эфф = 2πΔƒ_эфф – эффективная полоса частот сигнала.

Графически эффективная полоса частот представляет собой основание прямоугольника с высотой N_max и площадью, равной площади, ограниченной кривой спектральной плотности мощности сигнала и осью ординат.

Рис. 9.7

.