«Анализ параметров эвольвентного зубчатого колеса полученного методом обкатки» Порядок выполнения работы и расчётов:

Исходные данные:

№ - номер прибора (указан на рейке)

m – модуль зацепления в мм. (указан на рейке)

d – величина делительного диаметра (указан на рейке)

α_w – угол зацепления в градусах (указан на рейке)

До выполнения работы, необходимо произвести расчёты, указанные в таблице 1:

1. Рассчитать число зубьев обрабатываемой шестерни z = d/m

2. Определить коэффициент смещения ξ = (17 – z)/17

3. Вычислить величину смещения x = ξ ∙ m в мм

После получения нарезанной заготовки, необходимо произвести:

4. Вычисление и учёт геометрических параметров обработанного зубчатого колеса, указанных в таблице с указанием названия указанных параметров и их размерности.

В конце отчёта, выполненного курсантом в тетради для лабораторных работ, необходимо сделать выводы о проделанной работе с указанием на рисунке полученных параметров с корегированными и обычными колёсами.

Таблица 1.2.

Основные геометрические характеристики нарезанного зубчатого колеса

№ п/п	Параметры и их расчётные формулы	Нарезаемое зубчатое колесо
		некоррегирован-ное	коррегированное
	Диаметр заготовки dзк1 = d + 2m, мм.
	Диаметр заготовки dзк2 = (d + 2m)-x, мм.
	Делительный диаметр D = m ∙ z1, мм.
	Основной диаметр D0 = D ∙ cos αw, мм.
	Коэффициент смещения ξ = (17 – z)/17
	Величина смещения x = ξ ∙ m, мм.
	Высота головки зуба ha = (1 +x)∙m, мм.
	Высота ножки зуба hf = (1,25 − x)∙m, мм.
	Диаметр головки зуба da = d + 2ha, мм.
	Диаметр ножки зуба df = d – 2hf , мм.
	Окружной шаг p = m∙π, мм.

Выводы:

Выполнил курсант II курса гр. №_________

Работу проверил доц. ­­­­­­­­­­­­­­­­­­­­­___________________ Севастеев Д.И.

Лабораторная работа №2. Опредепение коэффициента полезного действия винтовых пар

Цель работы: Определение влияния типа резьбы и осевой нагрузки на КПД (η) винтовой пары

Исходные положения:

При рассмотрении сил в винтовой паре удобно резьбу развернуть по среднему диаметру d₂ в наклонную плоскость, а гайку заменить ползуном (см. рис. 2.1, а).

Рис.2.1. Силы взаимодействия между винтом и гайкой

Сила взаимодействия наклонной плоскости с ползуном при относительном движении представляет собой равнодействующую нормальной силы и силы трения. Следовательно, эта сила наклонена к нормали n под углом трения φ.

В результате разложения силы получаем

F_t = F ∙tg (ψ+ φ), (2.1)

где F_t — движущая окружная сила; F — осевая сила на винте; ψ — угол подъема резьбы; φ − угол трения.

Окружная сила трения в треугольной резьбе больше, чем в прямоугольной резьбе. Соотношение окружных сил трения в прямоугольной и треугольной резьбах удобно рассмотреть на моделях с кольцевыми витками, приняв угол подъема резьбы равным нулю (рис.2.1, б).

Окружная сила трения для витка прямоугольного профиля

F_t = F∙f; (2.2)

для витка треугольного профиля

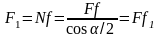(2.3)

где N = F/cos α/2;

α — угол профиля резьбы (см. рис. 2.1, б),

Из выражения (2.3) f₁, именуемый приведенным коэффициентом трения, будет равен:

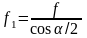. (2.4)

Таким образом, силу трения в треугольной резьбе можно определить так же, как в прямоугольной, только вместо действительного коэффициента трения надо пользоваться приведенным, равным действительному, деленному на cos α/2.

Аналогичное соотношение имеет место между углами трения:

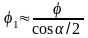. (2.5)

Для нормальной метрической резьбы угол α/2 = 30°, а следовательно, f₁≈1,15f и φ₁ ≈ 1,15φ.

Для определения движущей окружной силы в треугольной резьбе можно пользоваться выведенной формулой (1) для прямоугольной резьбы, подставив вместо действительного приведенный угол трения.

Момент завинчивания гайки или винта с головкой

Т_зав = Т_р + Т_т , (2.6)

где Т_р — момент в резьбе; Т_т — момент трения на торце гайки или головки винта.

Момент в резьбе

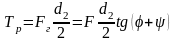. (2.7)

где d₂ =(d + d₀)/2

d – наружный диаметр резьбы;

d – внутренний диаметр резьбы;

φ – угол трения между телом гайки и винта;

ψ – угол подъёма резьбы.

Опорную поверхность гайки и головки принимают кольцевой с наружным диаметром, равным раствору ключа «а», и внутренним диаметром, равным диаметру отверстия под винт - d₀.

Момент трения на торце гайки или головки

Т_т = F∙f∙d_ср/2, (2.8)

Эта удобная для расчета зависимость основана на предположении, что давление на торце гайки увеличивается с уменьшением радиуса. Увеличение давления связано с упругим деформированием тела гайки и уменьшенными путями трения на малых радиусах при завинчивании и отвинчивании.

Момент на торце гайки или головки винта составляет около 50 % всего момента затяжки.

Подставив полученные выражения Т_р и Т_т в формулу для момента завинчивания, получим окончательно

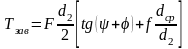. (2.9)

Приближенное геометрическое подобие резьб позволяет для ориентировочных расчетов пользоваться простейшими соотношениями, выведенными для средних значений параметров.

В качестве средних значений для нормальной метрической резьбы можно принять: ψ ≈ 2⁰30'; d₂ ≈ 0,9d; d_ср ≈ l,4d.

Тогда при f₁ = 0,15, характерном для резьбы без покрытий,

Т_зав ≈ 0,2 F∙d.

Расчетная длина ручного гаечного ключа может быть принята равной в среднем 14d.

Приравняв момент на ключе от силы F_р руки к моменту на винте, получаем соотношение между осевой силой на винте F и силой на рукоятке ключа F_р:

F ≈ 70F_р.

При коэффициенте трения f₁ = 0,1, характерном, в частности, для кадмированных смазанных винтов при сборке,

F ≈ 100F_р.

Таким образом, в крепежных резьбах можно получить выигрыш в силе в 70...100 раз. |

КПД резьбы определяется как отношение полезной работы на винте к затрачиваемой работе на ключе при повороте на произвольный угол. Для простоты и общности вывода удобно рассматривать поворот на малый угол dγ, при котором силы даже в условиях затяжки крепежных резьб можно считать постоянными.

КПД собственно резьбы без учета трения на торце

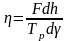(2.10)

где dh — осевое перемещение, соответствующее повороту на угол dγ.

Подставив в последнюю формулу ранее выведенное выражение для момента в резьбе Т_р и значение

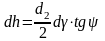. (2.11)

получаем

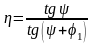. (2.12)

При ψ = 2⁰30' и f = 0,1 η ≈ 0,3.

КПД винта с учетом трения на торце

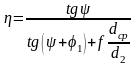. (2.13)

Момент, необходимый для отвинчивания гайки или винта с головкой, получают аналогично моменту завинчивания, только знак угла подъема меняют на обратный:

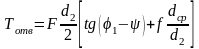. (2.14)

При отсутствии трения на торце гайки второй член должен быть отброшен.

Условия самоторможения Т_отв ≥ 0; отсюда для резьбы без трения на торце гайки tg (φ₁— ψ) > 0 и, следовательно, ψ < φ₁.

Для нормальных метрических резьб с углом подъема около 2°30' самоторможение даже при отсутствии трения на торце гайки наступает при φ₁≥ 2°30' т. е. при f₁ > 0,045.

При наличии трения на торце гайки и d_ср = l,4d самоторможение наступает при f₁ ≥ 0,02.

Таким образом, при статическом действии нагрузки имеются большие запасы надежности затяжки. Однако в условиях вибрационных нагрузок возможно ослабление затяжки резьбы, во избежание которого применяют специальные стопорные устройства.

Исследование коэффициента трения и коэффициента полезного действия винтовых пар проводится на испытательной установки, представленной на рис.2.1, кинематическая схема которой представлена на рис.2.2.

Испытательная установка имеет следующие характеристики:

Электродвигатель асинхронный на 110 в., мощностью 0,64 кВт; с частотой вращения ω_дв = 1440 об/мин.;

Редуктор: цилиндрический, соосный с передаточным числом u = 24

Электрический двигатель может быть включён только через специальный понижающий трансформатор дающий напряжение 110 В.

Таблица 2.1