
- •Вариант № 1
- •Вариант № 2
- •Вариант № 3
- •Вариант № 4
- •Вариант № 5
- •Вариант № 6
- •Вариант № 7
- •Вариант № 8
- •Найти область определения функции .
- •Вычислить пределы числовых последовательностей:
- •Вычислить пределы функций:
- •Вариант № 9
- •Вариант № 10
- •Вариант № 11
- •Вариант № 12
- •Вариант № 13
- •Вариант № 14
- •Вариант № 15
Вариант № 10
Найти область определения функции y=log4(x2+2x–15).
Построить график функции y=–ctgx+1.
Доказать, что
 исходя
из определения предела числовой
последовательности.
исходя
из определения предела числовой
последовательности.Вычислить пределы числовых последовательностей:
1)![]() ;
3)
;
3)
![]() ;
;
2)
![]() ;
4)
;
4)
![]() .
.
Вычислить пределы функций:
1)
![]() ;
7)
;
7)
![]() ;
;
2)
![]() ;
8)
;
8)
![]() ;
;
3)
![]() ;
9)
;
9)
![]() ;
;
4)
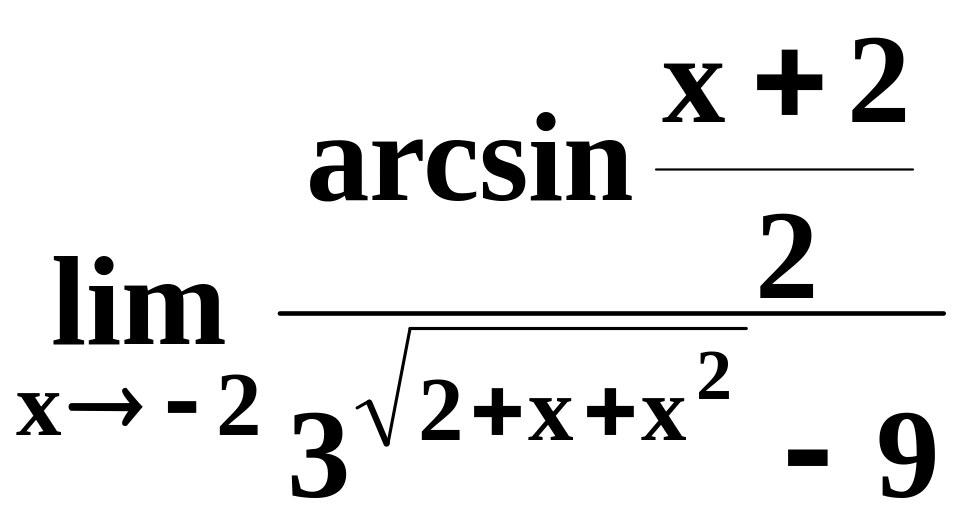 ;
10)
;
10)
![]() ;
;
5)
![]() ;
11)
;
11)
![]() ;
;
6)
![]() ;
12)
;
12)
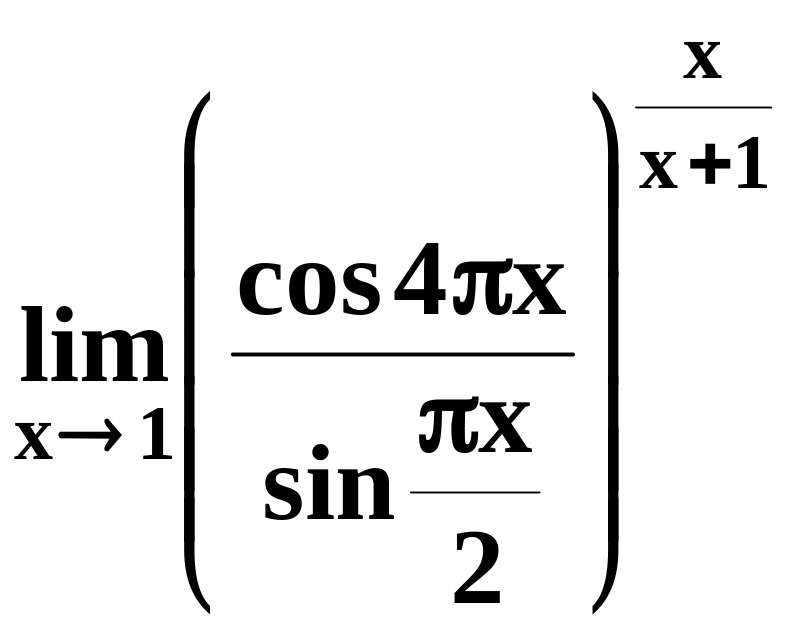 .
.
Доказать, что функция y=–4x2+9x–1 непрерывна в точке x0=4.
Найти точки разрыва следующих функций, указать характер разрыва и построить графики этих функций:
1)
![]() ;
2)
;
2)
![]()
Вариант № 11
Найти область определения функции y=arcsin(x–2).
Построить график функции

Доказать, что
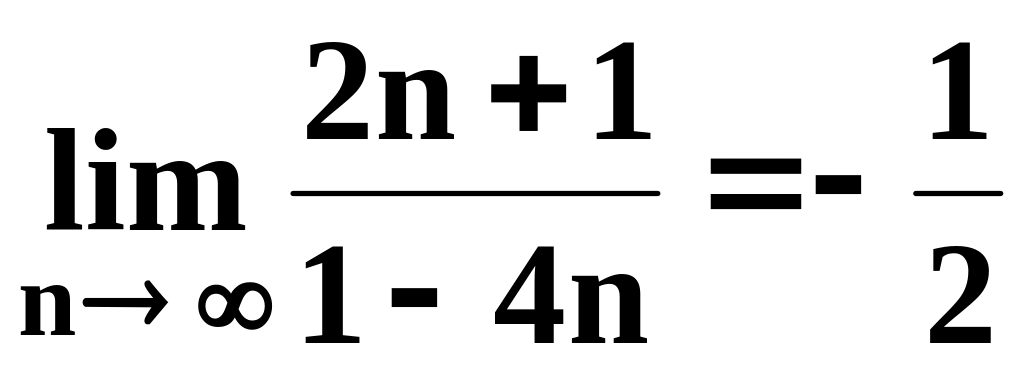 исходя из определения предела числовой
последовательности.
исходя из определения предела числовой
последовательности.Вычислить пределы числовых последовательностей:
1)
![]() ;
3)
;
3)
![]() ;
;
2)
![]() ;
4)
;
4)
![]() .
.
Вычислить пределы функций:
1)
![]() ;
7)
;
7)
![]() ;
;
2)
;
8)
![]() ;
;
3)
![]() ;
9)
;
9)
![]() ;
;
4)
![]() ;
10)
;
10)
![]() ;
;
5)
![]() ;
11)
;
11)
![]() ;
;
6)
![]() ;
12)
;
12)
![]() .
.
Доказать, что функция y=–3x2+5 непрерывна в точке x0=5.
Найти точки разрыва следующих функций, указать характер разрыва и построить графики этих функций:
1)
![]() ;
2)
;
2)
![]()
Вариант № 12
Найти область определения функции
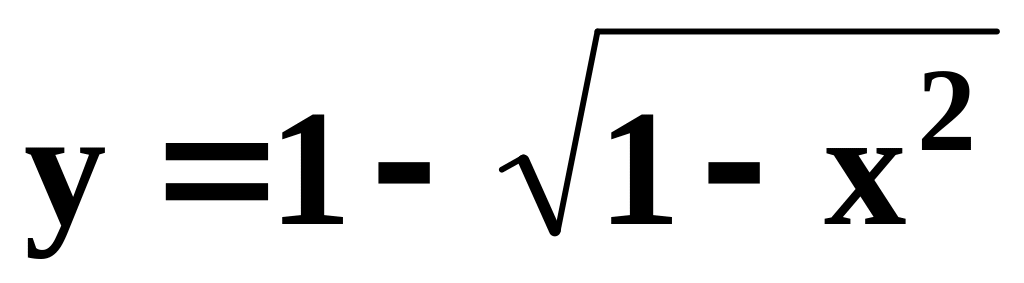 .
.Построить график функции:
 .
.Доказать, что
 исходя из определения предела числовой
последовательности.
исходя из определения предела числовой
последовательности.Вычислить пределы числовых последовательностей:
1)
![]() ;
3)
;
3)
![]() ;
;
2)
![]() ;
4)
;
4)
 .
.
Вычислить пределы функций:
1)
![]() ;
7)
;
7)
![]() ;
;
2)
![]() ;
8)
;
8) ;
;
3)
![]() ;
9)
;
9)
![]() ;
;
4)
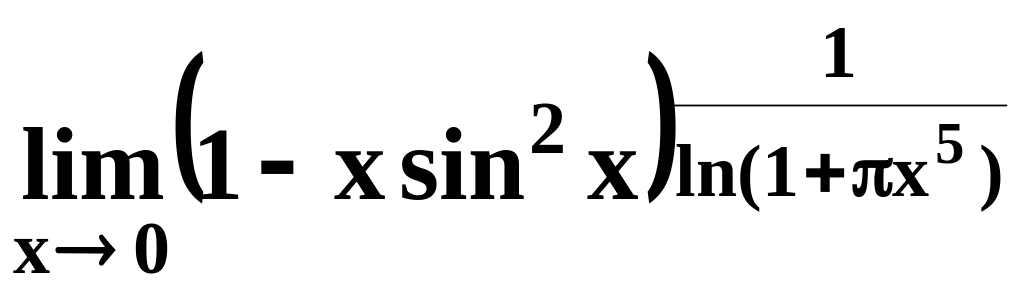 ;
10)
;
10)
![]() ;
;
5)
![]() ;
11)
;
11)
![]() ;
;
6)
![]() ;
12)
;
12)
![]() .
.
Доказать, что функция
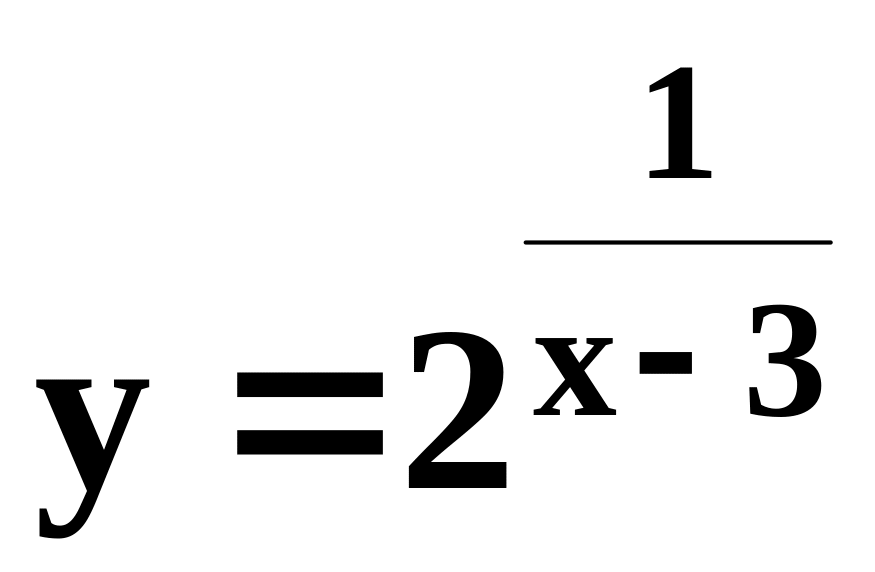 непрерывна в точке x0=5.
непрерывна в точке x0=5.Найти точки разрыва следующих функций, указать характер разрыва и построить графики этих функций:
1)
![]() ;
2)
;
2)
![]()
Вариант № 13
Найти область определения функции
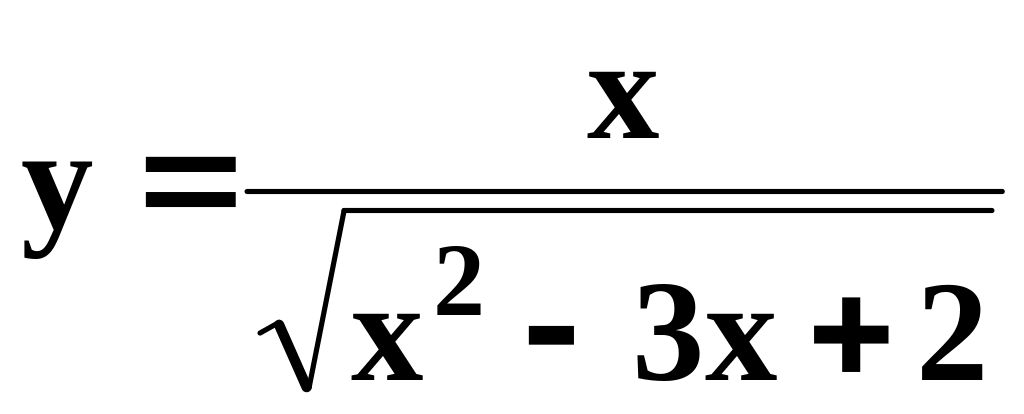 .
.Построить график функции y=arctg2x+1.
Доказать, что
 исходя
из определения предела числовой
последовательности.
исходя
из определения предела числовой
последовательности.Вычислить пределы числовых последовательностей:
1)
![]() ;
3)
;
3)
![]() ;
;
2)
![]() ;
4)
;
4)
![]() .
.
Вычислить пределы функций:
1)
![]() ;
7)
;
7)
![]() ;
;
2)
![]() ;
8)
;
8)
 ;
;
3)
![]() ;
9)
;
9)
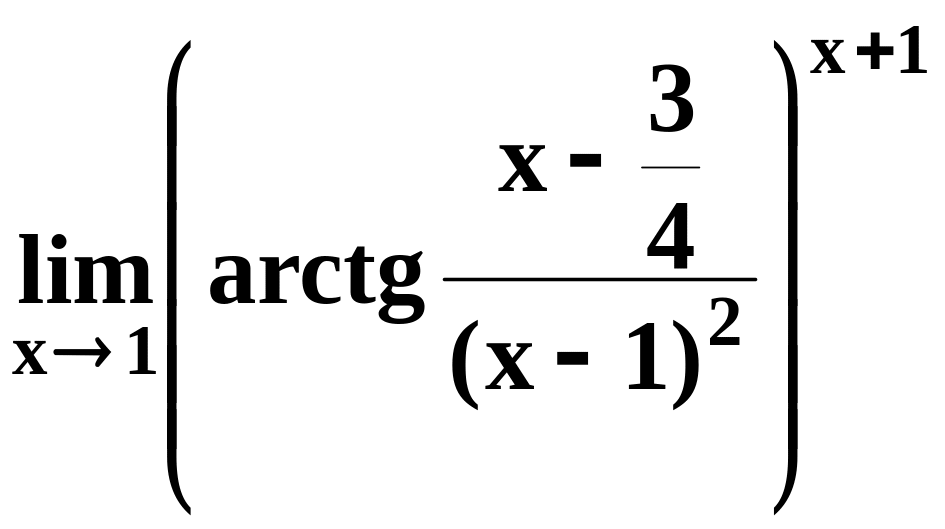 ;
;
4)
![]() ;
10)
;
10)
 ;
;
5)
![]() ;
11)
;
11)
![]() ;
;
6)
![]() ;
12)
.
;
12)
.
Доказать, что функция
 непрерывна
в точке x=2.
непрерывна
в точке x=2.Найти точки разрыва следующих функций, указать характер разрыва и построить графики этих функций:
 ,
2)
,
2)
