3.2.1.2. Аналитические модели однородных пакетных логических соединений уровня атм

Для однородных пакетных ИТС расчет сетевых характеристик логического соединения уровня АТМ сводится к расчету параметров «типичного» для сети –звенного составного канала. Математическая модель, описывающая процесс передачи трафика классов и по однородному транспортному каналу в пакетной ИТС-АТМ, может быть представлена однолинейной многофазной СМО с ожиданием и абсолютным приоритетным обслуживанием (с дообслуживанием) речевых ячеек по отношению к ячейкам данных на каждой фазе). Каждый канал ЛЦТ совместно с соответствующей ему частью памяти маршрутизаторов моделируется СМО . Внутри класса могут быть организовано либо раздельное обслуживание различных типов трафика с относительным приоритетом обслуживания индивидуальных очередей, либо обслуживание всех типов трафика в режиме FIFO в одной очереди с равным приоритетом.

Для вывода выражений коэффициентов загрузки и межсетевого уровня соответственно речевыми -ячейками и ячейками данных класса , которые учитывают динамику очередей разнородных пакетов на межсетевом уровне, сделаем следующие допущения и предположения:

• суммарные потоки на входе каждого канала тракта независимы друг от друга и являются простейшими;

• допустимое время сквозной задержки речевых ячеек в транспортном канале включает в себя только две основные компоненты: время накопления информационной части в оконечной системе источника, связанное с накоплением информационного поля ячейки в речепреобразующем устройстве (на передаче ( - )/ и время задержки в тракте передачи . Последнее включает случайную задержку пакетов в маршрутизаторах, обусловленную а) обслуживанием пакетов в поле коммутации, связанным с анализом таблиц маршрутизации и обработкой ячеек в коммутационных элементах (зависит от величины суммарного входящего потока и производительности связных процессоров); б) обслуживанием планировщиком пакетов (определяется объемом выходного буфера, дисциплиной обслуживания исходящей очереди и скоростью передачи в ЛЦТ). Заданное среднее время пребывания в тракте передачи ячеек класса также содержит время накопления информационной части у абонента, равное ( - )/ и . Отсюда возникает ограничение на величины и , которое необходимо учитывать при решении задачи параметрического анализа сети;

• в общем балансе времени и мы не будем учитывать время, затраченное на «последней миле» или в сети абонентского доступа , задержку распространения сигнала в физической среде и задержку на стороне получателя в депакетизаторе, связанной с компенсацией величины флуктуации сетевой задержки для обеспечения непрерывного воспроизведения речевых фрагментов на приеме.

На рисунке 3.1 представлена модель однородного логического соединения пакетной ИТС-АТМ на уровне АТМ в режиме установленного соединения.

Рисунок 3.1. Модель однородного логического соединения уровня АТМ в пакетной ИТС-АТМ

Однородный -звенный транспортный канал представляет собой последовательно включенных однородных межузловых ЛЦТ от источника до получателя (этот параметр учитывает качество маршрутизации информации в сети и ее топологию). На физическом уровне ЛЦТ образуют составной тракт передачи. При сделанных допущениях определим выражения для коэффициентов загрузки , . Максимальный коэффициент загрузки тракта ячейками трафика класса можно определить из следующих соображений. Пусть - время пребывания пакета в одном ЛЦТ составного VBRrt-канала передачи, тогда общее время пребывания -ячейки в -звеном VBRrt-канале передачи есть . Известно, что преобразование Лапласа плотности распределения времени пребывания -ячейки в -звеном VBRrt-канале, каждое звено которого моделируется СМО типа для любой пары имеет вид . В частности, если тракт передачи однороден, то для и

, (3.7)

где - величина, обратная средней длительности обслуживания речевой ячейки в -ой СМО типа ; - максимальная загрузка этой системы пропущенным речевым трафиком. Обращение преобразования (3.7) дает плотность распределения вероятности времени пребывания -ячейки в сквозном VBRrt-канале: . Отсюда получаем уравнение для нахождения максимально допустимой величины :

, (3.8)

Обозначив и произведя замену переменных в уравнении (3.8), получим

, (3.9)

Здесь

, (3.10)

где . По определению левая часть уравнения (3.9) есть неполная гамма-функция , следовательно

(3.11)

По аргументу справедливо следующее функциональное уравнение

. (3.12)

Для любого уравнение (3.11) с учетом рекуррентного соотношения (3.12) имеет вид:

, (3.13)

а условие существования его решения при условии есть [11]

(3.14)

Если это условие не выполняется, то при заданных и трафик класса службой VBRrt принципиально не может быть обслужен.

Левая часть уравнения (3.13) есть полином степени -1 относительно переменной . Для решения приведенного выше трансцендентного уравнения (3.13) может быть построена итерационная процедура, для чего прологарифмировав это уравнение и разрешив его относительно , получим

.

Можно показать, что нелинейный оператор, стоящий в правой части этого уравнения – сжимающий. Следовательно, возможно построение итерационной процедуры

, =0,1,2… (c начальным значением ). В пределе

. (3.15)

Именно таким способом были получены значения , приведенные в табл. 3.1.

Таблица 3.1.

Значения корня трансцендентного уравнения

n	2	3	5	7	10	13	15
0,005	7,4301	9,2738	12,5941	15,6597	19,9984	24,1450	26,8360
0.01	6,6384	8,4059	11,6046	14,5706	18,7831	22,8208	25,4461
0,03	5,3559	6,9838	9,9610	12,7466	16,7312	20,5730	23,0800

Из выражения (3.36) легко получить выражение для максимальной загрузки VBRrt-соединения речевыми -ячейками с учетом потерь

= . (3.16)

Известно, что среднее время пребывания меченного требования из класса в СМО типа , с учетом введенных выше приоритетов для трафиков классов и дается выражением

.

Общее среднее время пребывания ячейки данных в -звенном однородном ABR-канале передачи, включая задержку, связанную с накоплением информационной части ячейки в оконечной системе, дается выражением

= + , (3.17)

где = . Для однородного -звенного ABR-канала и дается выражением

= . (3.18)

Отметим, что в отличие от низкоскоростных и среднескоростных ЦСИС в ИТС на технологии АТМ восстановление поврежденных сообщений данных осуществляется только на уровне AAL. На подуровне сегментации и сборки AAL, формируется единый протокольный блок уровня (48-байтный сегмент), который на уровне AТМ упаковывается в 53-байтные ячейку. В цифровом тракте любая ячейка передается единым образом вне зависимости от типа информации.

Текущее значение в формулах (3.8), (3.10), (3.17) и (3.18) можно вычислить следующим образом. Пусть текущая нагрузка в канале равна = (эрл), где - суммарная речевая нагрузка, создаваемая в тракте в рамках устанавливаемых мультимедийных соединений Учитывая введенные ранее обозначения можно определить эффективную скорость переноса речевого трафика в 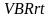-тракте, как

, (3.19)

где , - коэффициенты, учитывающие соответственно процедуру уплотнения пауз в речевых соединениях и способы сжатия речевых сигналов. С другой стороны минимальная эффективная скорость передачи речевого трафика в -тракте определяется выражением = . Откуда получаем ограничение на максимально возможную удельную загрузку

= (3.20)

Критерии эффективности использования однородных логических пакетных соединений уровня АТМ даются следующими выражениями

= (3.21)

= ( ). (3.22)