Тема: модель парной регрессии

Подгонка кривой

Регрессия – это односторонняя, стохастическая зависимость одной случайной переменной от другой, или нескольких случайных переменных.

Односторонняя стохастическая зависимость выражается с помощью функции, которая для отличия ее от строгой математической функции, называется «функцией регрессии» или просто регрессией.

Пусть существует набор переменных x_t, y_t, t=1,…,n. Можно отразить пары (x_t, y_t) точками на плоскости xy.

y

y _t f (x_t, ) = +x_t

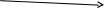отклонение y_t от f(x_t, β)

а

х_t x

Нашей задачей является подобрать («подогнать») функцию y = f(x) из параметрического семейства функций f(x,), наилучшим способом, описывающим зависимость y от х.

Подобрать функцию в данном случае означает выбрать наилучшее значение параметра . Примером параметрического семейства может служить семейство линейных функций f(x,)=+x.

«Наилучшую» аппроксимацию набора наблюдений x_t, y_t (t=1,…,n) линейной функции f(x) = a+bx, можно получить, используя известный метод наименьших квадратов.

Следует минимизировать функционал:

.

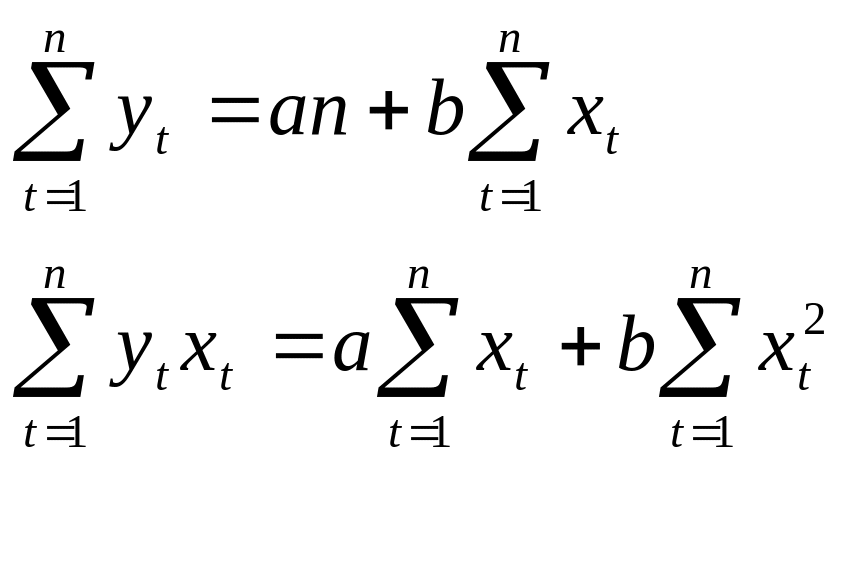
Пусть – решение этой системы:

.

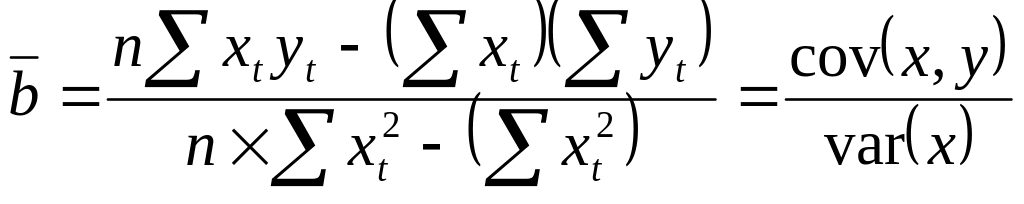
Замечание:

Ковариация или выборочная ковариация – это мера взаимосвязи между двумя переменными. Это число. Для его вычисления находятся средние значения параметров. Затем для каждого периода t вычисляются отклонения переменных от средних и перемножаются.

Если к требованию качества подгонки кривой добавить некоторые статистические свойства данных, то можно говорить об эконометрической модели. Дело в том, что на самом деле для каждого «х» мы можем наблюдать разные значения , “y”.

Мы уже говорили, что эконометрическая модель в виде регрессионного уравнения имеет вид:

где:

X_t – неслучайная (детерминированная) экзогенная величина;

ε_t – случайная величина;

y_t – объясняющая зависимая переменная;

x_t – объясняющая, независимая переменная, регрессор.

А уравнение, соответственно, называется регрессионным; y_t – регрессант.

Будем считать, что ε_t – случайная величина, с некоторой функцией распределения, которой соответствует функция случайной величины y_t.

Основные гипотезы

1. y_t=a+bx_t+ε_t, t=1,…,n - спецификация модели (уже провели подгонку кривой).

2. X_t – детерминированная величина, вектор (x₁,…,x_n)^T – неколлинеарен вектору S=(1,…,1)^T, состоящему из одних единиц.

3. Математическое ожидание Е ε_t=0.

1. E(δ_t)²=V(ε_t)=δ², и не зависят от t.

2. E(ε_t,δ_s)=0, t≠s - некоррелированность ошибок для разных наблюдений.

3. ε_t~N(0,δ²) – имеет нормальное распределение; ε_t – нормально распределенная величина со средним, равным 0, и дисперсией δ². В этом случае модель называется нормальной, линейной, регрессионной.

Л И Т Е Р А Т У Р А

1. Доугерти К. Введение в эконометрику. Издание второе. Перевод с английского. -М.: ИНФРА, 2007.

2. Магнус Я.Р., Катышев П.К., Пересецкий А.А. Эконометрика. Начальный курс. Учебник. -М.: «Дело», 2005.