2.3. Моделирование взаимосвязей в детерминированном факторном анализе

Одной из задач факторного анализа является моделирование взаимосвязей между факторами и результативными показателями, сущность которого состоит в том, что эта взаимосвязь выражается в форме математического уравнения.

Выделяют следующие типы факторных моделей:

- аддитивная модель – модель сложения и вычитания: результативный показатель представляет собой алгебраическую сумму или разность нескольких факторов:

Y = ΣXi = X₁ + X₂ + X₃ + …+ X_n;

- мультпликативная модель – модель умножения: результативный показатель представляет собой произведение нескольких факторов:

Y = X₁ * X₂ * X₃ * …* X_n;

- кратная модель – модель деления: результативный показатель получают делением одного факторного показателя на величину другого.

Y = ;

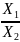- смешанная (комбинированная) модель – сочетание в разных комбинациях предыдущих моделей:

Y = ; Y = ; Y = 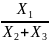и т.д.

С целью получения новых, более развёрнутых вариантов моделей, позволяющих глубоко и комплексно по выявленным факторам исследовать результативный показатель, производят преобразование детерминированных систем. Для этой цели используют следующие приёмы: расширение моделей, удлинение моделей, сокращение моделей.

Моделирование мультипликативных факторных систем осуществляется путём расширения модели. Расширение мультипликативных факторных моделей – это процедура расчленения факторов исходной системы на факторы-сомножители. Например, двухфакторный результативный показатель объёма производства продукции (VВП) рассчитывается умножением среднегодовой численности персонала (ЧР) на среднегодовую выработку работника (ГВ):

VВП = ЧР * ГВ.

Годовую выработку можно представить как произведение количества дней, отработанных одним рабочим за год (Д) и среднедневной выработки (ДВ), тогда модель станет трёхфакторной:

VВП = ЧР * Д * ДВ.

Дневная выработка, в свою очередь, рассчитывается умножением продолжительности смены (П) на среднечасовую выработку (ЧВ). Подставив значения в формулу, модель становится четырёхфакторной:

VВП = ЧР * Д * П * ЧВ.

Степень детализации и расширения модели зависит от цели исследования, возможностей детализации и формализации показателей в пределах установленных правил.

Моделирование аддитивных факторных систем также осуществляется путём расчленения факторов исходной модели на составные элементы.

Известно, что прибыль от реализации продукции (П_рп) рассчитывается вычитанием из выручки (В) расходы, связанные с производством и реализацией продукции (Р):

П_рп = В – Р.

Но также известно, что расходы состоят из себестоимости реализованной продукции (С), суммы коммерческих расходов (КР), суммы управленческих расходов (УР). Тогда исходную модель можно записать следующим образом:

П_рп = В – С – КР - УР.

К классу кратных моделей применяют следующие способы их преобразования: удлинения, расширения, сокращения.

Способ удлинения – это процедура разложения числителя исходной модели на сумму отдельных факторов:

Y = 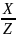= = a * b * c * d/

Например, результативный показатель издержкоёмкости (затраты на 1 рубль произведённой продукции) рассчитывается делением суммы затрат на объём произведённой продукции. Если числитель этой дроби представить суммой отдельных элементов затрат, то в результате преобразования модель принимает вид:

ИЕ = 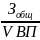= = М_е + Т_е + А_е + d_н.р.,

где ИЕ – издержкоёмкость;

З_общ – общая сумма затрат;

МЗ – материальные затраты;

ТР – трудовые затраты;

АЗ – амортизационные затраты;

НР – накладные расходы;

М_е – материалоёмкость продукции;

Т_{е –} трудоёмкость (зарплатоёмкость);

А_е – амортизационная ёмкость;

d_н.р – уровень накладных расходов на один рубль продукции.

Способ расширения состоит в умножении числителя и знаменателя исходной модели на один или несколько новых показателей. Так, если в исходную модель Y = a/b ввести новый показатель с, то модель примет вид:

Y = = =

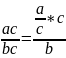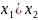
Например, если числитель и знаменатель рентабельности активов умножить на показатель выручки от реализации, модель примет вид:

,

где 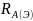- рентабельность активов;

П_р – прибыль от реализации;

А – среднегодовая величина капитала, активов;

В – выручка от реализации;

R_об – рентабельность реализации (продаж);

К_об – коэффициент оборачиваемости активов.

Способ сокращения состоит в создании новой факторной модели путём деления числителя и знаменателя дроби на один и тот же показатель, в результате чего получается модель исходного типа, но с другим набором факторов.

Известно, что фондоотдача рассчитывается делением выручки на среднегодовую стоимость основных средств: Ф_о = В / .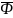

Если числитель и знаменатель разделить на среднесписочную численность работников, то получим кратную модель, но с новым набором факторов: производительности труда и фондовооруженности труда:

= ,

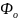
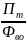где Ф_о – фондоотдача;

В – выручка от реализации продукции;

– среднегодовая стоимость основных средств;

Чр – среднесписочная численность работников;

П_т – производительность труда;

Ф_во – фондовооруженность труда.

Способ формального разложения – знаменатель исходной модели раскладывается на сумму или произведение отдельных факторов:

Y = .

Например, рентабельность (окупаемость) затрат можно представить в виде модели:

где

П – прибыль;

МЗ – материальные затраты;

ТЗ – трудовые затраты;

АЗ – амортизационные отчисления;

НР – накладные расходы.

Необходимо отметить, что моделирование факторных систем – очень сложный и ответственный процесс. От того, насколько реально и точно созданные модели отражают взаимосвязь между исследуемыми показателями, зависят конечные результаты анализа.

Вопросы для самоконтроля

1. Охарактеризуйте метод и методику экономического анализа.

2. Назовите основные приёмы и способы, используемые в экономическом анализе.

3. Перечислите источники информации для проведения экономического анализа.

4. Что понимается под факторным анализом? Каковы задачи факторного анализа?

5. Назовите основные виды классификации факторов в экономическом анализе.

6. Перечислите типы факторных моделей в детерминированном анализе.

7. Назовите приёмы моделирования взаимосвязей в детерминированном факторном анализе. Как производится моделирование?