
- •Описание экспериментальной установки.
- •Порядок выполнения работы
- •1. Определение плотности жидкости.
- •2. Определение плотности твердых тел.
- •Ход выполнения работы.
- •1. Определение плотности жидкости.
- •2. Определение плотности твердого тела.
- •Контрольные вопросы.
- •Порядок выполнения работы
- •Контрольные вопросы
- •Литература
- •Лабораторная работа №6 измерение длин
- •Линейный нониус
- •Штангенциркуль
- •М икрометр
- •Измерительный микроскоп
- •Лабораторная работа №6’ изучение прецизионного измерителя длин иза – 2
- •С пиральный нониус
- •Лабораторная работа №7 точное взвешивание
- •1) Метод Гаусса, 2) метод тарирования, 3) метод постоянной нагрузки.
- •1. Метод двойного взвешивания (метод гаусса)
- •2. Метод тарирования
- •3. Метод постоянной нагрузки (метод менделеева)
- •Задание 1
- •Задание 2
- •Задание 3
- •Задание 4
- •Описание экспериментальной установки
- •Порядок выполнения работы
- •Контрольные вопросы
- •Литература
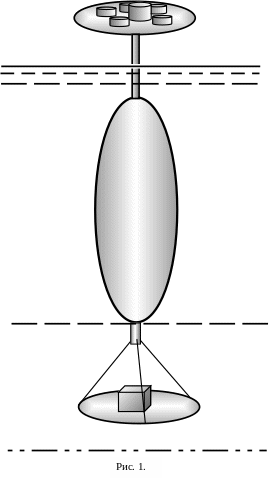
- •Лабораторная работа №10 определение плотности жидкостей и твердых тел гидростатическим взвешиванием
- •Лабораторная работа №11 измерение сопротивлений мостовым методом
- •Описание экспериментальной установки
- •Размеры трифилярного подвеса
- •Методика проведения эксперимента
- •Зависимость напряжения от температуры
- •Лабораторная работа №15 изучение движения маятника максвелла
- •Краткая теория
- •Описание экспериментальной установки
- •Порядок проведения эксперимента
- •Контрольные вопросы
- •Лабораторная работа №16 определение момента инерции тел методом крутильных колебаний
- •Краткая теория.
- •Описание экспериментальной установки.
- •Выполнение работы.
- •Порядок проведения эксперимента.
- •Порядок проведения эксперимента.
- •К онтрольные вопросы.
- •Лабораторная работа №17 проверка второго закона ньютона с помощью вращающейся платформы
- •Лабораторная работа №18 изучение равноускоренного движения тел на машине атвуда
- •Краткая теория
- •Описание установки (вариант 1)
- •Экспериментальная установка методика проведения эксперимента
- •Краткие теоретические сведения
- •Описание экспериментальной установки
- •Ход выполнения работы
- •Контрольные вопросы
- •Рекомендуемая Литература
- •Лабораторная работа №28 определение скорости звука в воздухе с помощью интерферометра
- •Краткие теоретические сведения
- •Описание лабораторной установки
- •План подготовки к работе
- •Методика проведения эксперимента
- •Контрольные вопросы.
- •Литература
- •Описание экспериментальной установки
- •Метод непосредственного наблюдения
- •2. Дифракционный метод
- •Описание установки
- •Градуировочная таблица
- •Ход выполнение работы
- •Контрольные вопросы
- •Рекомендуемая литература
- •Лабораторная работа определение плотности жидкости с помощью пикнометра
- •Рекомендуемый биоблиографический список
Контрольные вопросы.
1. Дайте определение массы, веса, плотности и удельного объема тела.
2. От каких параметров они зависят?
3. От каких причин зависит точность определения плотности тел ареометром постоянного объема?
4. Каковы преимущества и недостатки ареометра постоянного объема?
ЛИТЕРАТУРА.
1. Лабораторные работы под редакцией Зильбермана А.Н.
2. Савельев И.В. Курс общей физики. т,1.
ЛАБОРАТОРНАЯ РАБОТА №3
ОПРЕДЕЛЕНИЕ РАДИУСА КРИВИЗНЫ
ВОГНУТОЙ ПОВЕРХНОСТИ МЕТОДОМ КАТАЮЩЕГОСЯ ШАРИКА
Цель работы: Определить радиус кривизны вогнутой сферической поверхности и произвести оценку погрешности полученного результата.
Принадлежности: Вогнутое сферическое зеркало, стальные шарики, секундомер, штангенциркуль.
КРАТКАЯ ТЕОРИЯ
Движение шарика, катящегося по плоской поверхности, можно представить в виде векторной суммы двух движений: 1) поступательного со скоростью с, равной скорости его центра масс, 2) вращательного вокруг оси, проходящей через центр масс, с угловой скоростью .
Скорость любой точки шарика относительно поверхности определится соотношением
.![]() . (1)
. (1)
Если качение шарика происходит без проскальзывания, то скорость его точки B, соприкасающейся с поверхностью, будет равна нулю. В силу этого, как следует из (1) (см. рис.1), 0 = с - r. Поэтому
![]() ,
(2)
,
(2)
где r - радиус шарика.
С помощью формул (1) и (2), можно подсчитать скорость любой точки шарика. Так, например, скорость точки А равна 2с.
Шарик, помещенный на вогнутую поверхность, занимает положение, соответствующее минимуму его потенциальной энергии. Если шарик вывести из этого положения и отпустить, то он будет колебаться около своего положения равновесия. Качение шарика без проскальзывания возможно при действии на него со стороны поверхности силы трения покоя (силы трения сцепления) F (рис.2). Эта сила F может принимать любое значение от 0 до N , где - коэффициент трения, N – величина нормальной реакции поверхности. При качении сила F принимает такое значение, при котором скольжение отсутствует. Если сила требующаяся для этого, превышает величину N , то чистое качение невозможно - оно будет сопровождаться проскальзыванием.
Покажем, что на вогнутой сферической поверхности при небольших смещениях от положения равновесия, шарик будет совершать гармонические колебания. Результирующая сил, действующих на шарик (силы трения сцепления F , нормальной реакция поверхности N и силы тяжести mg) сообщает центру масс шарика некоторое ускорение, которое можно представить в виде векторной суммы нормального an и тангенциального a ускорений:
![]() .
(3)
.
(3)
Проектируя (3) на направление касательной к траектории шарика, получим:
![]()
Если ограничиться малыми углами, при которых sin , то будем иметь:
![]() .
(4)
.
(4)
Результирующий момент сил, действующих на шарик, сообщает ему угловое ускорение , которое входит в основное уравнению динамики вращающихся твердых тел
![]() .
(5)
.
(5)
Уравнение (5) описывает вращение шарика относительно оси, проходящей через его центр масс. Здесь Ic - момент инерции шарика относительно оси, проходящей через центр масс, - его угловое ускорение шарика, Fr - момент силы трения сцепления относительно указанной оси. (Моменты сил mg и N относительно указанной оси равны нулю). Для однородного шара
![]() .
(6)
.
(6)
Если радиус кривизны сферической поверхности R существенно превосходит радиус шарика r, то связь между ускорениями a и может быть представлена соотношением:
![]() (7)
(7)
Подставляя (6) и (7) в (5), получим:
![]() .
(8)
.
(8)
Исключая величину F из формул (4) и (8), можно получить:
![]() .
.
Принимая во внимание, что
![]() ,
,
где S - смещение шарика от положения равновесия, отсчитанное по траектории центра масс шарика, R - радиус кривизны этой траектории , получим:
![]() .
(9)
.
(9)
Из полученного следует, что тангенциальное ускорение шарика пропорционально его смещению от положения равновесия и направлено к положению равновесия. Это указывает на то, что колебания шарика будут гармоническими.
В самом деле, при гармоническом колебании смещение S изменяется по закону
S = Acost
Дифференцируя S дважды по t, получим:
![]()
![]() (10)
(10)
Здесь
![]() - циклическая частота колебания.
- циклическая частота колебания.
Из формул (9) и (10) следует, что
![]()
В результате для радиуса кривизны траектории центра масс шарика R получим
![]() .
(11)
.
(11)
Радиус кривизны вогнутой поверхности зеркала будет превышать R на величину радиуса шарика r. Поэтому
Rз=R + r . (12)
Чтобы получить более точное выражение для радиуса кривизны сферического зеркала необходимо учесть, что путь S, проходимый центром масс шарика и длина дуги l, описываемая точкой B, не равны другу. Как следует из рис. 2,
l= Rз, S= (Rз-r) и кроме того l=r
Дифференцируя приведенные соотношения дважды по t, и принимая во внимание, что тангенциальная составляющая ускорения центра масс шарика a и его угловое ускорение соответственно равны;
![]() и
и
![]() ,
,
получим формулу, связывающую их между собой
![]() (7’)
(7’)
Используя вместо (7) формулу (7’), получим более точное выражение для радиуса кривизны зеркала
![]() (12’)
(12’)
