Порядок проведения эксперимента.

1. Закрепить на раме однородный прямой круговой цилиндр так, чтобы его продольная ось, проходящая через центр масс цилиндра, совпадала с вертикальной осью маятника. Определить время 20 колебаний маятника. Рассчитать период колебаний маятника Т_ц .

2. Закрепить на раме однородный стальной шар и определить время 20 колебаний маятника. Рассчитать период колебаний маятника Т_ш .

3. Определить массы цилиндра, шара и куба. Штангенциркулем измерить радиусы цилиндра R , шара R и ребро куба a.

4. Найти отношение моментов инерции исследуемых тел

на основе данных о периоде колебаний крутильного маятника

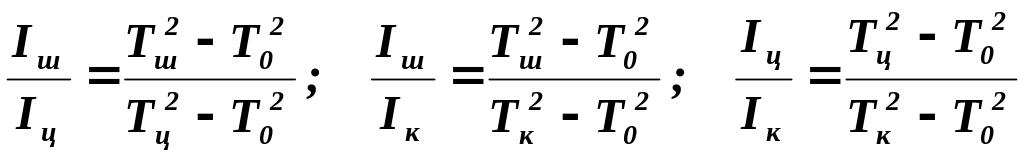
и сравнить полученные значения с теми, которые можно получить с помощью формул (5 - 7). Оценить ошибку результатов. Сделать выводы.

К онтрольные вопросы.

1. Какую физическую величину называют моментом инерции? Какое свойство тел характеризует момент инерции? Каковы единицы измерения момента инерции в СИ и СГС системах?

2. Приведите формулы, в которые входит момент инерции.

3. Сформулируйте теорему Штейнера.

4. Объясните механизм возникновения крутильных колебаний.

ЛИТЕРАТУРА.

1. Савельев И.В. Курс общей физики. т.1 §§37-42, 65, 1968.

2. Фриш С.Э., Тиморева А.В. Курс общей физики. т.1, §§34-37, 1958.

3. Архангельский М.М. Курс общей физики. Механика. гл. 9, §§3-6, 1975.

4. Александров Н.Я., Яшкин А.Я. Курс общей физики. Механика. 1978, с. 223-232,

Лабораторная работа №17 проверка второго закона ньютона с помощью вращающейся платформы

Цель работы: Экспериментальная проверка второго закона Ньютона.

Оборудование: Вращающаяся платформа, динамометр, набор грузов, электронный блок для измерения времени.

КРАТКИЕ ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ

В основе классической механики лежат три закона Ньютона. Они являются результатом обобщения большого эмпирического материала.

Первый закон Ньютона утверждает, что в природе существуют такие системы отсчета, относительно которых тело движется равномерно и прямолинейно или находится в состоянии покоя, если на него не действуют другие тела. Эти системы отсчета называют инерциальными системами отсчета (ИСО). Системы отсчета, в которых не выполняется первый закон Ньютона, называют неинерциальными системами отсчета (НИСО).

Второй закон Ньютона указывает на характер движения тела в ИСО в случае, когда на тело действуют другие тела.

Второй закон Ньютона утверждает, что тело изменяет свое состояние (свою скорость) только тогда, когда на него действуют другие тела. Мерой действия тел друг на друга является сила, величина которой определяется соотношением

. (1)

Как видим, второй закон Ньютона вводит в физику две новые величины – силу являющуюся мерой действия тел друг на друга, и массу m, характеризующую инертность тела. Под инертностью понимают способность тела оказывать "сопротивление" воздействующим на него телам. Эти две величины входят в одно и то же уравнение, которое не может быть разрешено, пока не указаны независимые способы определения одной из них. Для разрешения этой проблемы массу одного из тел устанавливают произвольно. Это тело называют эталоном массы. Масса эталона принята равной 1 кг. Массу других тел находят путем сопоставления с массой эталона. Как показывает опыт, при одинаковом воздействии на тела величина произведения для каждого их них одна и та же.

Поэтому будет справедливо соотношение

,

в котором m _зт – масса эталона, а_эт – его ускорение, m – масса исследуемого тела, а – его ускорение.

Как показал впервые Галилей, все тела вблизи поверхности Земли в отсутствие сил сопротивления со стороны воздуха падают на Землю с одинаковым для всех тел ускорением, которое называют ускорением свободного падения g. Силу, которая сообщает телу ускорение свободного падения, называют силой тяжести. Величина силы тяжести определяется формулой

.

Указанное обстоятельство обеспечивает возможность измерения массы тел с помощью рычажных весов. При равновесии весов результирующий момент сил тяжести равен 0. Поэтому

m _зт g L_зт = m g L,

где L_эт и L – длины плеч сил тяжести. Таким образом,

m = m_эт (L_эт /L).

При равноплечии весов (L_эт = L)

m = m_эт.

Здесь m – масса взвешиваемого тела, m_эт – масса разновесков (масса эталона).

Первоначально масса отождествлялась с количеством вещества в теле. В силу этого не возникал вопрос о зависимости массы от скорости тела. Однако количество вещества, связанное с данным телом, и его инертность представляют собой две совершенно разные физические величины. В настоящее время их четко различают и измеряют разными физическими величинами: количество вещества измеряют в молях (штуках), а массу – в килограммах (кг).

Вопрос о зависимости массы от скорости тела вначале был разрешен теоретически на базе постулатов специальной теории относительности (релятивистской механики). В результате было показано, что масса тела возрастает с возрастанием его скорости по закону

.

Здесь m_о – масса покоя  – скорость тела, c – скорость света в вакууме.

Выводы специальной теории относительности полностью подтверждены экспериментами, выполненными на ускорителях частиц.

Следует заметить, однако, что в последние годы произошел пересмотр прежних представлений о зависимости массы тела от скорости. В настоящее время принято считать, что от скорости зависит энергия тела, в частности за счет возрастания его кинетической энергии. Зависимость энергии тела от скорости определяется соотношением

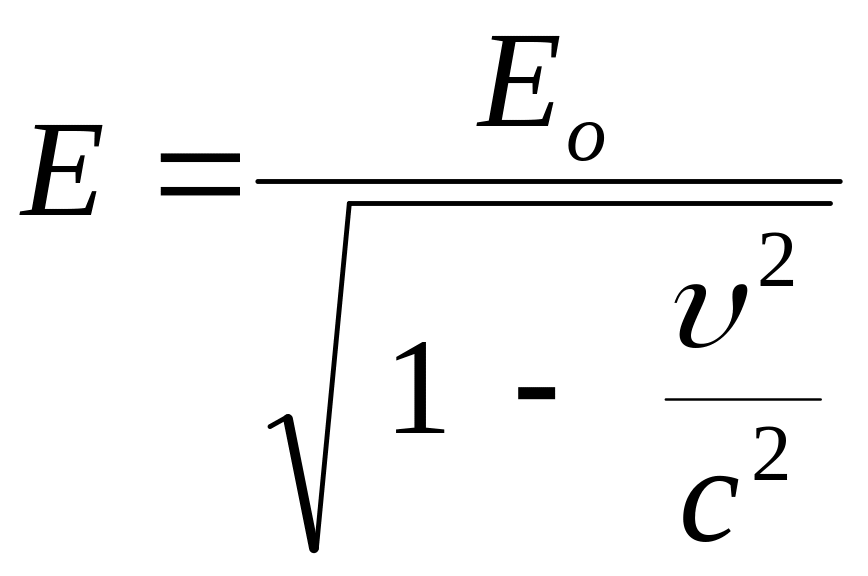. (2)

Как и ранее, величина E_o = m_oc², представляет собой энергию, связанную с массой покоя, а величина энергии E = E_o + К, где К – кинетическая энергия тела, обусловленная его движением. При скоростях движения много меньших скорости света   c величина кинетической энергии К = E − E_o определяется известным из механики Ньютона выражением

.

В современной интерпретации физический смысл имеет только масса покоя, которую легко определить простым взвешиванием. Поэтому

m  m_o.

Подвесим тело на пружине. Пружина при этом растянется до некоторой длины L, и возникшая при деформации пружины сила упругости уравновесит силу тяжести

F_упр = mg.

Как показывает опыт, в пределах упругости каждому значению длины пружины L однозначно соответствует определенное значение возникшей при деформации силы упругости. Таким образом, оказывается возможным построить прибор, измеряющий силу по величине деформации пружины. Этот прибор называют динамометром. Градуировка динамометра существенно упрощается в силу справедливости закона Гука. В соответствии с законом Гука величина силы упругости прямо пропорциональна удлинению пружины

F_упр = k L . (3)

Здесь k – коэффициент жесткости пружины, L – ее удлинение.

Таким образом, величину силы можно измерить либо по величине деформации пружины, либо по величине ускорения, которое она сообщает телу.

Теперь рассмотрим эмпирические факты, приводящие к формулированию второго закона Ньютона в форме соотношения (1).

Подействуем на два разных тела одной и той же пружиной (одной и той же силой), растянутой до длины L₁ , и измерим ускорения тел a₁ и a₂. Подействуем на эти тела пружиной, растянутой до длины L₂. Ускорения тел при этом изменятся и станут равными a₁^‘ и a₂^’. Однако отношение ускорений останется прежней величиной

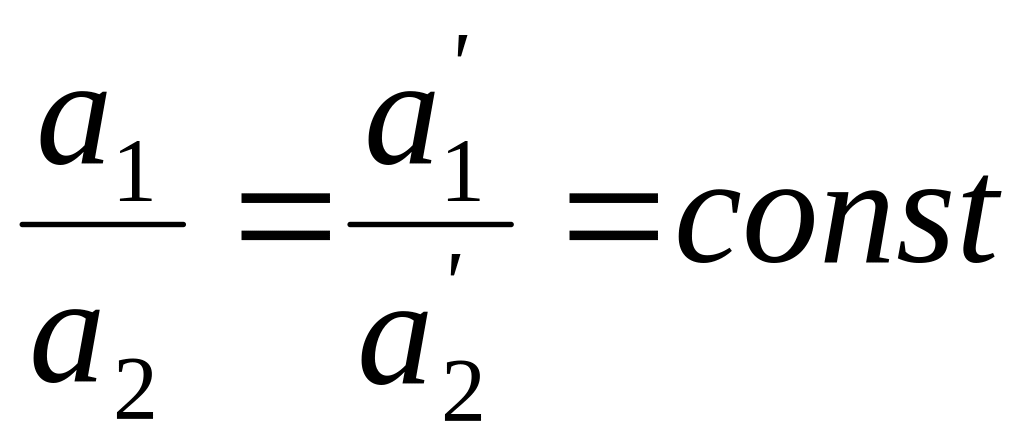. (4)

Отношение ускорений останется неизменным и тогда, когда пружина будет растянута до длины L₃, L₄… Таким образом, можно прийти к выводу о том, что отношение ускорений данных двух тел не зависит от величины действующих на них одинаковых сил. Оно является характеристикой их внутренних свойств – характеристикой их инертности. Если в формуле (4) константу заменить отношением масс тел

,

то при одинаковом воздействии на тела величина ma для них будет одна и та же и может служить мерой действия на тела других тел (в данном случае растянутой – пружины). Эту величину и называют силой:

m₁a₁ = m₂a₂ = F .

Сила является векторной величиной. Направление силы определяет направление ускорения тела:

.

Если на тело действуют несколько тел, то результирующая сила определяется как векторная сумма сил, действующих со стороны каждого тела в отдельности:

. (5)

Приведенное соотношение (5) является математическим выражением принципа независимости действия сил (принципа суперпозиции сил).

Выполнение описанных выше опытов представляет собой достаточно сложную экспериментальную задачу. Это связано с тем, что на движущиеся тела всегда действует не одна, а несколько сил, точный учет которых весьма затруднителен. В первую очередь это относится к силам сопротивления, действующим со стороны окружающих тел. Поэтому первоначальные экспериментальные факты связывались с движением планет и их спутников. В результате были открыты кинематические законы движения планет (законы Кеплера). Как известно, планеты, близкие к Солнцу, движутся практически по круговым орбитам и испытывают нормальное (центростремительное) ускорение. Это ускорение обусловлено действием силы тяготения со стороны Солнца. Его сравнительно легко вычислить.

Эксперименты с телами, движущимися равномерно по круговым траекториям, весьма плодотворны и в земных условиях, так как позволяют локализовать траекторию движения тела и упростить процедуру измерения его ускорения, которое при равномерном движении по окружности является центростремительным ускорением и определяется формулой

.

Измерение нормального ускорения, как видим, сводится к измерению периода обращения тела T и расстояния его от оси вращения R.

В рассматриваемом в работе случае исследуемые тела помещаются на равномерно вращающемся диске. Они имеют цилиндрическую форму и могут катиться практически без трения скольжения вдоль направляющего ребра, укрепленного на диске. Сила трения качения при большом радиусе цилиндров чрезвычайно мала. Сравнительно просто решается вопрос о силе, сообщающей телу нормальное ускорение. Этой силой является сила упругости, величина которой зависит от величины деформации пружины динамометра. Вполне естественно предположить, что при одной и той же деформации пружины возникающие силы упругости имеют одну и ту же величину.

Если второй закон Ньютона справедлив, то отношение нормальных ускорений исследуемых тел при любых одинаковых силах, действующих на тела со стороны пружины динамометра, будет одним и тем же. Проводимые опыты должны подтвердить это и привести к выводу о том, что отношение ускорений тел обратно отношению квадратов периодов обращения диска и зависит только от отношения масс исследуемых тел:

.

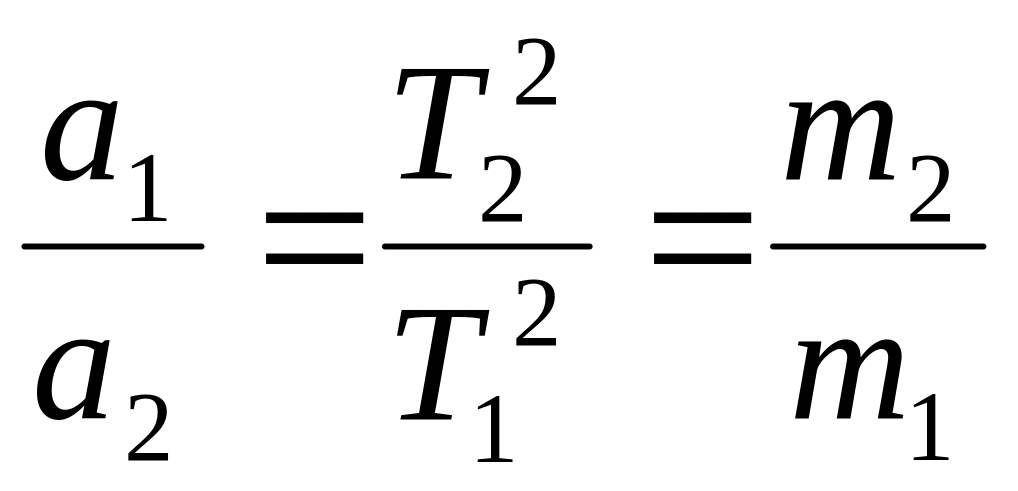Другими словами, выполненные измерения должны показать, что при одинаковых силах, действующих на тела, периоды обращения диска T₁ и T₂ связаны между собой прямой пропорциональной зависимостью

с коэффициентом пропорциональности k, равным корню квадратному из отношения масс исследуемых тел.

Систему аксиом классической механики завершает третий закон Ньютона.

Третий закон Ньютона утверждает, что два тела взаимодействуют между собой с силами, равными по величине, действующими вдоль одной прямой в противоположные стороны. Из третьего закона следует, что силы возникают парами при взаимодействия тел и имеют одну природу. Эти силы приложены к разным телам и потому не уравновешивают друг друга.

ОПИСАНИЕ ЭКСПЕРИМЕНТАЛЬНОЙ УСТАНОВКИ

Основной частью установки (рис. 1) является вращающийся относительно вертикальной оси металлический диск 1. Вдоль радиуса диска укреплено направляющее ребро 2 , на котором помещаются исследуемые тела 3 цилиндрической формы.

Ц илиндрическая форма тел обеспечивает возможность перемещаться вдоль направляющего ребра диска с минимальным трением. Удержание тел на заданном расстоянии от оси вращения осуществляется с помощью легкой нерастяжимой ленты 4, выполненной из прочного пластического материала. Эта лента через легкий неподвижный блок связывает тело с динамометром 5, укрепленным над центром диска. Величина деформации пружины динамометра, от которой зависит величина силы упругости, определяется по углу отклонения стрелки динамометра.

Угловая скорость вращения диска может изменяться в широких пределах путем изменения напряжения, подаваемого на зажимы электродвигателя, вращающего диск. Величина напряжения измеряется вольтметром, установленным на автотрансформаторе (ЛАТР). Напряжение на зажимах двигателя не должно превышать 100 В.

Для измерения периода обращения диска используется специальный электронный блок, имеющий световой датчик и электронные кварцевые часы, фиксирующие время t заданного числа оборотов N. Период обращения диска T определяется по формуле

Световой датчик располагают на удобном расстоянии от края диска так, чтобы специальные указатели (узкие металлические пластинки), смонтированные на диске, полностью перекрывали световой луч дважды в течение периода обращения диска T. Измерение времени t производится с точностью до 0,002 с.

ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ

1. Изучить конструкцию установки и подготовить ее к работе.

2. Поместить на направляющее ребро 2 исследуемое тело большей массы и соединить его с динамометром гибкой лентой 4. В исходном положении стрелка динамометра должна находиться вблизи нулевого штриха его шкалы.

3. Постепенно увеличить напряжение, подаваемое на зажимы электродвигателя, плавно раскручивая диск до скорости, при которой стрелка динамометра отклонится на 2–3 деления шкалы. Добиться равномерного вращения диска при выбранной величине отклонения стрелки динамометра. Определить время 2–5 полных оборотов диска. Опыт повторить 3–5 раз. При этом строго следить за тем, чтобы стрелка динамометра оставалась на одном и том же месте шкалы. Удобнее всего с выбранным положением стрелки совместить нулевой штрих шкалы. Для выполнения указанной операции поворачивают шкалу динамометра. Для удержания стрелки динамометра в заданном положении осторожно, малыми порциями с помощью ЛАТР изменить напряжение на зажимах электродвигателя. Найти среднее значение времени t. Результаты занести в таблицу.

П р и м е ч а н и е. Перед пуском секундомера нажимают кнопку "СБРОС". Остановку секундомера производят нажатием кнопки "СТОП" сразу после того, как на счетчике оборотов появляется цифра, на единицу меньшая задаваемого значения.

4. Сбросить напряжение до 0 и остановить вращение диска. Поставить на диск другое тело меньшей массы. Раскрутить диск до такой скорости вращения, при которой отклонение стрелки динамометра станет равным ранее выбранной величине (будет совмещено с нулевым делением шкалы).

Определить время 2–5 полных оборотов диска. Опыт повторить 3–5 раз. Тщательно следить за тем, чтобы вращение диска было равномерным и положение стрелки динамометра при этом совпадало бы с нулевым делением шкалы.

При выполнении указанных условий сила, с которой пружина динамометра действует на тела в первой и второй серии опытов, будет одинаковой. Найти среднее значение времени t. Полученный результат занести в таблицу.

5. Увеличить скорость вращения диска, изменив напряжение на зажимах электродвигателя так, чтобы стрелка динамометра отклонилась на одно деление шкалы от своего прежнего значения. Совместить с новым положением стрелки нулевой штрих шкалы. Добившись равномерного вращения диска, определить время 2–5 полных оборотов диска в новых условиях. Опыт повторить 3–5 раз. Найти среднее значение t. Полученный результат занести в таблицу.

6. Сбросить напряжение до 0 и остановить диск. Поместить на диск тело большей массы. Довести скорость вращения диска до такой величины, при которой стрелка динамометра будет находиться вблизи нулевого штриха шкалы. Определить время 2–5 полных оборотов диска. Опыт повторить 3–5 раз. Найти среднее значение времени t. Полученный результат занести в таблицу.

7. Оставив на диске тело большей массы, выполнить операции, предусмотренные п. 5.

8. Выполнить операции, предусмотренные п. 6 для тела меньшей массы.

9. Оставив на диске тело меньшей массы, выполнить операции, предусмотренные п. 5.

10. Выполнить операции, предусмотренные п. 6 для тела большей массы.

11. Оставив на диске тело большей массы, выполнить операции, предусмотренные п. 5.

12. Выполнить операции, предусмотренные п. 6 для тела меньшей массы.

13. С помощью рычажных весов определить массы тел m₁ и m₂ c точностью до 1 г.

В результате проведенных измерений будет получено не менее 5 пар значений времени t₁ и t₂, а следовательно, и 5 пар значений периодов обращения диска T₁ и Т₂, полученных при 5 разных значениях силы упругости, действующей на исследуемые тела. Отношение этих периодов для каждого значения силы должно быть одним и тем же, равным корню квадратному из отношения масс исследуемых тел.

П р и м е ч а н и е. Для определения среднего значения отношения периодов диска T₁ и T₂ можно воспользоваться методом наименьших квадратов или построить график T₁= f(T₂), на котором величина искомого отношения периодов T₁ и T₂ будет равна тангенсу угла наклона прямой.

КОНТРОЛЬНЫЕ ВОПРОСЫ

1. Какое основное утверждение содержится во втором законе Ньютона?

2. Какое свойство тел характеризует масса тел?

3. Что такое сила?

4. В какой форме следует записывать второй закон Ньютона для неинерциальной системы отсчета?

5. Почему силы инерции называют фиктивными силами?

РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА

Савельев И.В. Курс общей физики. Т.1. – М.: Наука, 1968.

Сивухин Д.В. Общий курс физики. Механика. – М.: Наука, 1974.

Архангельский М.М. Курс физики. Механика. – М., 1975.