Задача 1.1 а. При измерении частоты сигнала F получены следующие результаты наблюдений Fi: 18.305, 18.308, 18.312, 18.309, 18.304,18.306, 18.309, 18.310, 18.303, 18.308, 18.306, 18.313, 18.305, 18.307,18.308, 18.309, 18.307, 18.309, 18.310, 18.308 кГц.

Считать, что генеральная совокупность отклонений результатов наблюдений распределена по нормальному закону.

Определить: результат измерения частоты F, значение среднеквадратического отклонения результатов наблюдений σ (исключить, если имеются промахи), значение среднеквадратической погрешности результата измерения σ_F, указать его доверительную вероятность Р; интервал случайных погрешностей ±Δp, с доверительной вероятностью Р=0.95.

- Рассчет результата измерения частоты .

- Рассчет среднеквадратического отклонения результатов наблюдений .

, где – абсолютная погрешность -го измерения.

кГц.

С целью установления промахов воспользуемся правилом «трех сигма» – если , то такой результат не является промахом. . Результаты вычислений представлены в таблице 1.

Таблица 1

, кГц	18.305	18.308	18.312	18.309	18.304	18.306	18.310	18.303
, кГц	0.006	0.008	0.004	0.007	0.005	0.007	0.006	0.004

Т.к. во всех случаях выражение больше нуля, то можно заключить, что грубых погрешностей нет.

- Рассчет среднеквадратической погрешности результата измерения .

кГц.

- Рассчет доверительной вероятности .

, где , .

После замены получаем следующее:

.

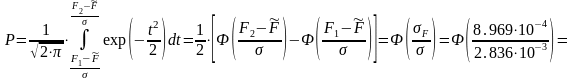
- Рассчет равновероятного интервала случайных погрешностей.

Т.к. число измерений мало ( ), то для нахождения интервала случайных погрешностей воспользуемся распределением Стьюдента, согласно которому . Для заданных доверительной вероятности и числа наблюдений , табулированное значение коэффициента Стьюдента . Следовательно:

кГц.

Задача № 1.1,б.

При измерении частоты сигнала были получены следующие результаты наблюдений : , , 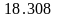, , , , , , , 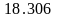кГц.

Считать, что генеральная совокупность отклонений результатов наблюдений распределена по нормальному закону.

Определить: результат измерения частоты , значение среднеквадратического отклонения результатов наблюдений (исключить, если имеются промахи), значение среднеквадратической погрешности результата измерения , указать его доверительную вероятность ; интервал случайных погрешностей с доверительной вероятностью .

• Рассчет результата измерения частоты .

кГц.

• Рассчет среднеквадратического отклонения результатов наблюдений .

, где – абсолютная погрешность -го измерения.

кГц.

С целью установления промахов воспользуемся правилом «трех сигма» – если , то такой результат не является промахом. . Результаты вычислений представлены в таблице 1.

Таблица 1

, кГц	18.305	18.308	18.312	18.309	18.304	18.306	18.310	18.303
, кГц	0.006	0.008	0.004	0.007	0.005	0.007	0.006	0.004

Т.к. во всех случаях выражение больше нуля, то можно заключить, что грубых погрешностей нет.

• Рассчет среднеквадратической погрешности результата измерения .

кГц.

• Рассчет доверительной вероятности .

, где , .

После замены получаем следующее:

.

• Рассчет равновероятного интервала случайных погрешностей.

Т.к. число измерений мало ( ), то для нахождения интервала случайных погрешностей воспользуемся распределением Стьюдента, согласно которому . Для заданных доверительной вероятности и числа наблюдений , табулированное значение коэффициента Стьюдента . Следовательно:

кГц.

Задача 1.1г

При измерении частоты сигнала F получены следующие результаты наблюдений F_i: 18.305, 18.308, 18.312, 18.309, 18.304.

Считать что генеральная совокупность отклонений результатов наблюдений распределена по нормальному закону.

Определить результат измерения частоты F, значение среднеквадратического отклонения результатов наблюдений σ (исключить, если имеются промахи) значение среднеквадратичной погрешности результата измерения σ_F указать его доверительную Вероятность P; интервал случайных погрешностей ±Δ_P с доверительной вероятностью P = 0.95.

Решение:

Условно результатом измерения частоты будем считать, усреднение всех результатов по времени

Определим абсолютное отклонение:

Частота	Абсолютное отклонение
18.305	-0.03
18.308	0.00
18.312	0.04
18.309	0.01
18.304	-0.04

Среднеквадратическое отклонение.

По определению среднеквадратичное отклонение это есть

Находим несмещенную оценку среднеквадратичного отклоненного.

Находим оценку среднеквадратичного отклонения.

Оценим уровень значимости коэффициентов

Откидываем все которые меньше единицы, находим соответственно