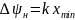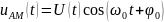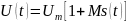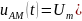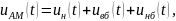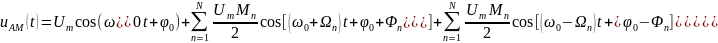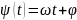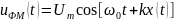- •1 Элементы общей теории электрических сигналов
- •1.1 Математическая модель сигнала
- •1.2 Импульсные сигналы
- •1.3 Аналоговые, дискретные и цифровые сигналы
- •1.4. Динамическое представление сигналов
- •1.5 Линейное пространство сигналов
- •10 Координатный базис
- •20 Понятие нормы в линейном пространстве сигналов
- •30 Метрика линейного пространства
- •40 Скалярное произведение в пространстве сигналов
- •1.6 Обобщенный ряд Фурье
- •1.7 Спектральное представление сигналов
- •1.9 Спектральная плотность сигнала. Преобразование Фурье
- •1.10 Обратное преобразование Фурье
- •1.11 Спектральные плотности абсолютно интегрируемых функций
- •Дельта-функция
- •1.12 Частные случаи и следствия спектральных представлений
- •1.13 Некоторые свойства спектральных плотностей и сигналов
- •70. Формула Релея:
- •1.14 Спектральные плотности сигналов, не являющихся абсолютно интегрируемыми
- •1.15 Модулированные сигналы
- •1.16 Амплитудная модуляция
- •1.17 Сигналы с угловой модуляцией
- •1.18 Фазовая модуляция (фм)
- •Мгновенная частота сигнала
- •1.19 Частотная модуляция (чм)
- •2 Сигналы с ограниченным спектром
- •2.1 Построение математических моделей сигналов с ограниченным спектром
- •2.4.2 Теорема Котельникова – Шеннона
- •2.4.3 Оценка ошибки, возникающей при аппроксимации произвольного сигнала рядом Котельникова
- •2.4.4 Геометрическая интерпретация сигналов, ограниченных по спектру и длительности
1.15 Модулированные сигналы
В МБИ и в используемых технических средствах встречаются сложные модулированные сигналы, обеспечивающие лучшую помехоустойчивость передаваемых сообщений.
Несущее
колебание:
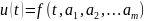 ,
где параметры
,
где параметры
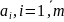 определяют форму колебания.
определяют форму колебания.
Если
по крайней мере один параметр
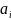 изменяется по закону передаваемого
сообщения
,
то несущее колебание несет в себе
информацию, заключенную в передаваемом
сообщении.
изменяется по закону передаваемого
сообщения
,
то несущее колебание несет в себе
информацию, заключенную в передаваемом
сообщении.
Например,
сигнал
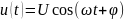 ,
являющийся простым гармоническим
колебанием, становится сложным колебанием,
если по закону
изменяются один или несколько его
параметров
,
являющийся простым гармоническим
колебанием, становится сложным колебанием,
если по закону
изменяются один или несколько его
параметров
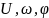 .
.
1.16 Амплитудная модуляция
Амплитудно-модулированный (АМ) сигнал, представленный на рис. 1.24, можно записать в виде
|
(1.59) |

Рис. 1.24 Гармонический сигнал, модулированный гармоническим сигналом.
Огибающая АМ-колебаний
|
(1.60) |
Здесь – полезный сигнал;
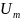 – постоянный
коэффициент, определяющий амплитуду
колебаний в отсутствие модуляции;
– постоянный
коэффициент, определяющий амплитуду
колебаний в отсутствие модуляции;
M – коэффициент модуляции.
Известны коэффициенты:
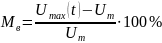 – относительный
коэффициент модуляции вверх.
– относительный
коэффициент модуляции вверх.
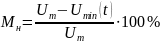 – относительный
коэффициент модуляции вниз.
– относительный
коэффициент модуляции вниз.
При
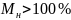 наступает
явление перемодуляция.
наступает
явление перемодуляция.
Простейший
вид
АМ-модуляции
– модуляция гармоническим колебанием
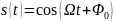 ,
в этом случае амплитудно-модулированный
сигнал
,
в этом случае амплитудно-модулированный
сигнал
|
(1.61) |
|
|
где
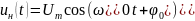 – несущее
колебание,
– несущее
колебание,
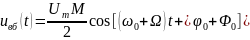 – верхнее
боковое колебание,
– верхнее
боковое колебание,
 – нижнее
боковое колебание.
– нижнее
боковое колебание.
На практике однотональная модуляция используется редко, реальные информационные сигналы имеют сложный спектральный состав.
В математической модели такого сигнала, представимого набором гармоник
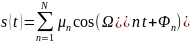 ,
,
амплитуды
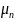 и начальные фазы
и начальные фазы
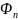 произвольны, а выражение для АМ
– сигнала
имеет вид
произвольны, а выражение для АМ
– сигнала
имеет вид
|
(1.62) |
или
|
(1.63) |
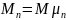 –
парциальные
коэффициенты модуляции.
–
парциальные
коэффициенты модуляции.
Спектральные плотности модулируюшего и промодулированного сигнала изображены на рис. 1.25.

Рис. 1.25 Спектральные плотности модулирующего S(Ω) и промодулированного S(ω) сигналов
Спектр
верхних боковых колебаний
повторяет низкочастотный спектр
 информационного сигнала, а спектр нижних
боковых колебаний повторяет его
зеркальную копию, т.е полезная информация
в спектре АМ
– сигнала
представлена дважды, в левой и в правой
от
частях.
При этом тратится значительная энергия
передающего устройства и занимается
излишне широкая полоса частотного
диапазона.
информационного сигнала, а спектр нижних
боковых колебаний повторяет его
зеркальную копию, т.е полезная информация
в спектре АМ
– сигнала
представлена дважды, в левой и в правой
от
частях.
При этом тратится значительная энергия
передающего устройства и занимается
излишне широкая полоса частотного
диапазона.
В практике широко применяются сигналы с одной боковой полосой (SSB-сигналы), а также с подавлением несущей частоты, которая восстанавливается в приемном устройстве.
1.17 Сигналы с угловой модуляцией
Угловая
модуляция осуществляется при изменении
в соответствии с передаваемым сообщением
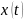 частоты несущих колебаний
частоты несущих колебаний
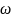 или фазы φ.
или фазы φ.
Полная фаза гармонического колебания
|
(1.63) |
1.18 Фазовая модуляция (фм)
Пусть
полная фаза
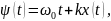
где k – коэффициент пропорциональности, – значение частоты при отсутствии полезного сигнала.
Сигнал с фазовой модуляцией имеет вид:
|
(1.64) |
На рис.1.26 показаны модулирующее и модулированное колебания.

Рис. 1.26 Модулирующий и модулированный по фазе сигналы
Предельное значение фазового сдвига называют девиацией фазы.
Верхняя
девиация фазы:
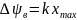
Нижняя
девиация фазы: