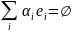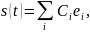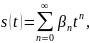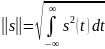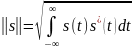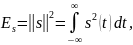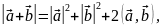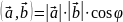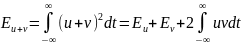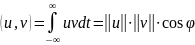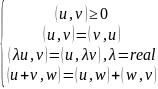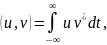10 Координатный базис

Координатный базис по аналогии с векторным пространством вводится как система линейно независимых сигналов 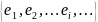, для которых

(1.6)

лишь в случае, когда все .

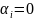Тогда сигнал можно разложить в координатном базисе

(1.7)

где C_i - проекции сигнала s(t) в базисе .

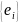Например, для сигналов, представляемых степенным рядом

базисом является совокупность сигналов

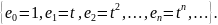
20 Понятие нормы в линейном пространстве сигналов

Пространство L является нормированным, если каждому сигналу сопоставлено число 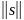- норма этого сигнала, и справедливы следующие свойства нормы:

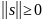-   (неотрицательна), 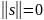тогда и только тогда, когда ;

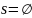-  для любого справедливо .

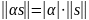-  если 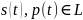, то справедливо неравенство треугольника

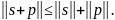
Используются несколько способов задания нормы:

(1.8)

– для вещественных аналоговых сигналов;

(1.9)

– для комплексных сигналов.

(1.8) называют энергетической формой представления нормы, потому что, возведенная в квадрат, она является энергией сигнала (на практике чаще всего о сигнале судят по энергетическому эффекту), т.к.

(1.10)

т. е. если через сопротивление в 1 Ом протекает ток , то E_s –энергия, выделяемая на этом сопротивлении.

Кроме того, при использовании интегральной формы нормы сглаживаются кратковременные случайные выбросы в полезном сигнале.

Если норма вводится в форме (1.8), то L называют пространством функций с интегрируемым квадратом и обозначают L₂.

30 Метрика линейного пространства

Пространство L становится метрическим, если каждой паре элементов 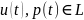сопоставлено неотрицательное число 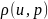– метрика (или расстояние между элементами), обладающая свойствами:

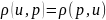– – рефлекcивность метрики,

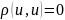– при любых ,

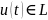– для любого .

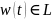
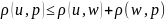Обычно метрику определяют как норму разности двух сигналов

(1.11)

Норму можно понимать как расстояние между выбранным элементом и нулевым элементом .

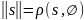Зная метрику можно судить, насколько хорошо один сигнал аппроксимирует другой.

40 Скалярное произведение в пространстве сигналов

Введя структуру, норму и метрику линейного пространства, мы все же не имеем возможность вычислять важную характеристику – угол между сигналами (векторами). Этот изъян устраняется, если ввести скалярное произведение, пользуясь соотношениями аналитической геометрии (рис. 1.8).

Известно, что

	(1.12)
где

Рис. 1.8 Представление суммы векторов в векторном (эвклидовом) пространстве

По аналогии с векторными представлениями выразим энергию суммы двух сигналов

(1.13)

Сравнивая (1.12) и (1.13), определим скалярное произведение двух сигналов 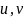как

(1.14)

И соответственно угол между двумя сигналами

(1.15)

Интеграл 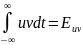называют еще взаимной энергией сигналов .

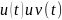Запишем для скалярного произведения 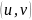очевидные свойства

(1.16)

Дополнения 1⁰…4⁰ совместно с основными аксиомами 1…4 обеспечивают универсальную конструкцию линейного пространства сигналов.

Линейное пространство со скалярным произведением (1.14)…(1.16) полное в том смысле, что содержит все свои предельные точки любых сходящихся последовательностей из этого пространства, называется вещественным гильбертовым пространством Н.

Если ввести комплексное скалярное произведение по формуле

(1.17)

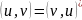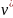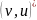а также равенство , то получим аналогичное определение комплексного гильбертова пространства. Здесь и – соответственно комплексно-сопряженные значения сигнала и скалярного произведения.

Сконструированное таким образом пространство сигналов позволяет формализовать работу с сигналами, упростить их анализ и синтез, а также решение задач исследования в целом.

Одной из таких задач в устройствах передачи и обработки информации является задача ортогонализации.

Два сигнала u и 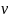называются ортогональными, если их скалярное произведение и, следовательно, взаимная энергия равна нулю

(1.18)

В практических расчетах при анализе сигналов удобнее пользоваться ортонормированным базисом, определяемым как система ортогональных функций, обладающих единичными нормами и скалярным произведением

(1.19)

Примеры ортогональных сигналов

1. Сигналы, разнесенные по времени, представлены на рис. 1.9.

Рис. 1.9 Ортогональные сигналы, разнесенные по времени

2. Сигналы, совмещенные по времени и удовлетворяющие условию (1.18), изображены на рис. 1.10.

Рис. 1.10 Ортогональные сигналы, совмещенные по времени