Электрические сигналы в медико-биологических исследованиях
1 Элементы общей теории электрических сигналов
Сигнал (Signum - знак, сообщение) это информация о состоянии материи. Можно рассматривать сигнал как форму физического состояния какого-либо объекта, или как проявление структуры материального объекта, или как форму состояния энергии и т.д.
В теории электрических сигналов принято считать сигналом процесс изменения во времени физического состояния какого-либо объекта, служащий для отображения, передачи и регистрации сообщений.
1.1 Математическая модель сигнала
Функциональную зависимость от времени f(t), s(t), u(t), ... ,
выраженную например формулой:
|
(1.1) |
а также в виде таблицы или базы данных, будем называть математической моделью сигнала.
В медико-биологических исследованиях, также как и в электротехнических, одна и та же модель может описывать ток, напряжение, напряжённость ЭМП и другие физические характеристики БО.
Сигналы
типа (1.1) являются одномерными, а
совокупность сигналов
,
объединенных по каким-либо признакам
называют многомерными (N
- размерность).
Если математическая модель позволяет точно предсказать мгновенные значения сигнала в любые моменты времени, то сигнал является детерминированным, если такое предсказание не возможно, то сигнал случайный.
Строго говоря, детерминированных сигналов нет. Но когда уровень случайной компоненты (помехи) мал по сравнению с полезным сигналом, такая идеализация оправдана.
1.2 Импульсные сигналы
Колебания, существующие лишь в пределах конечного отрезка времени называют импульсными (рис.1.1).К таковым можно отнести сигналы в электрокардиограмме, энцефалограмме, реограмме и в других сигналах при МБИ.
Основными
характеристиками такого сигнала являются
длительность импульса
,
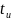длительности переднего фронта
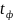и спада импульса
,
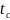а также его амплитуда
.
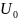Различают а)
видеоимпульсы
и б)
сигналы с заполнением или радиоимпульсы.
Рис.1.1 Импульсные сигналы: а) видеоимпульс, б) радиоимпульс (высокочастотный сигнал, модулированный видеоимпульсом)
В случае радиоимпульса, математическую модель которого можно представить в виде:
|
(1.2) |
появляются и другие важные характеристики сигнала:
—частота
и начальная фаза заполняющих высокочастотных
колебаний.
В
этом случае
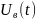называют огибающей радиоимпульса, а
—
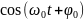высокочастотным заполнением радиоимпульса.
1.3 Аналоговые, дискретные и цифровые сигналы
Если при протекании физического процесса сигнал можно измерять в любые моменты времени, то сигнал называют аналоговым. График такого сигнала может быть непрерывным (рис.1.1), или содержать точки разрывов 1-го рода.
В технике часто применяются устройства, использующие дискретные сигналы (рис. 1.2).
Простейшая
модель дискретного сигнала –
это
счётное множество точек
,
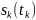определённых на множестве точек
.
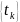Достоинство дискретных сигналов в том, что сигнал можно воспроизводить не во все моменты времени, при этом по одной и той же линии можно передавать сообщения от разных источников различным потребителям (многоканальная связь с разделением по времени).
Рис. 1.2 Дискретный
и цифровой сигналы
Разновидность дискретного сигнала – это цифровой сигнал в двоичной системе с ограниченным числом разрядов.
Строго говоря, любой дискретный или цифровой сигнал можно считать аналоговым.
Ниже, на рис. 1.3 показаны два способа дискретизации аналогового сигнала s(t).
Рис.2.3
Способы дискретизации аналогового
сигнала