Задание №4 тема: изгиб

Для балки построить эпюры внутренних силовых факторов используя метод сечений

Определить прогиб посередине балки используя правило Верещагина (энергетические способы определения перемещений). Жесткость балки определить исходя из размеров сечения и материала. Сечение двутавр №10

Дано:

а=1,4м q= 8кН/м Р=22,4 кН М= 31,36 кНм

Материал балки - Ст 10

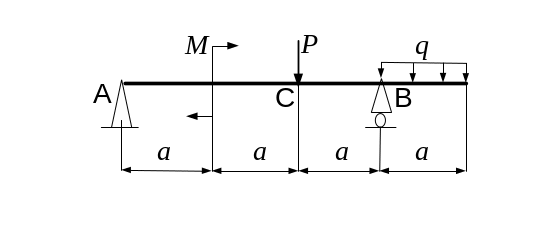
Рис.4 Схема балки

Решение:

1. Определяем опорные реакции, применяя уравнения равновесия статики:

Основная балка: (рис.4а)

Вспомогательная балка для определения прогиба: (рис.4б)

2. Разбиваем балку на 4 участка.

Применяя метод сечений, определяем значения поперечных сил Q_у и изгибающих моментов М_Х на участках балки

I участок: (0 £ z ₁ £ 1, 4)

Основная балка:

Вспомогательная балка для определения прогиба:

II участок: (1,4 £ z ₂ £ 2,8)

Основная балка:

Вспомогательная балка для определения прогиба:

III участок: (0 £ z ₃ £ 1,4)

Основная балка:

Вспомогательная балка для определения прогиба:

IV участок: (1,4 £ z ₃ £ 2,8)

Основная балка:

Вспомогательная балка для определения прогиба:

Эпюру поперечных сил и изгибающих моментов строим в масштабе:

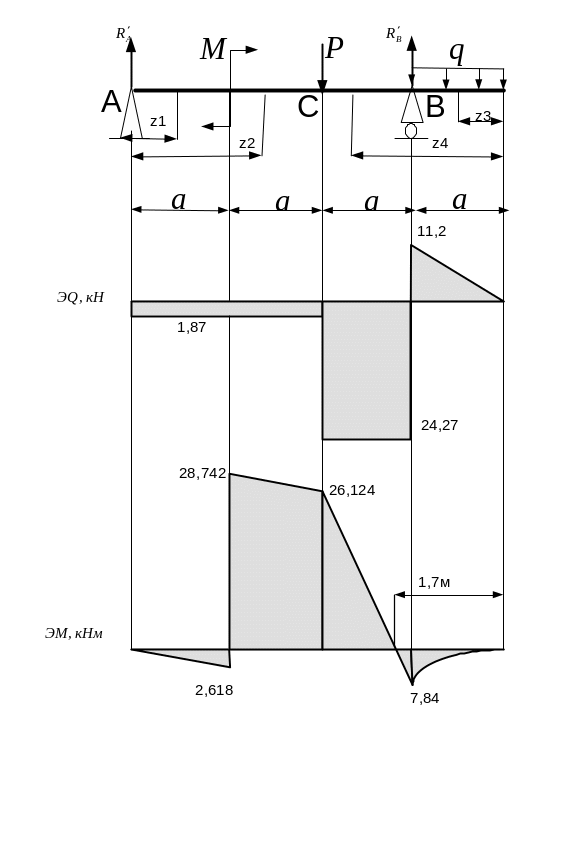
Эпюру изгибающих моментов М _х для основной и вспомогательной балки для определений прогиба строим в масштабе смотри рисунок 4в, 4г.

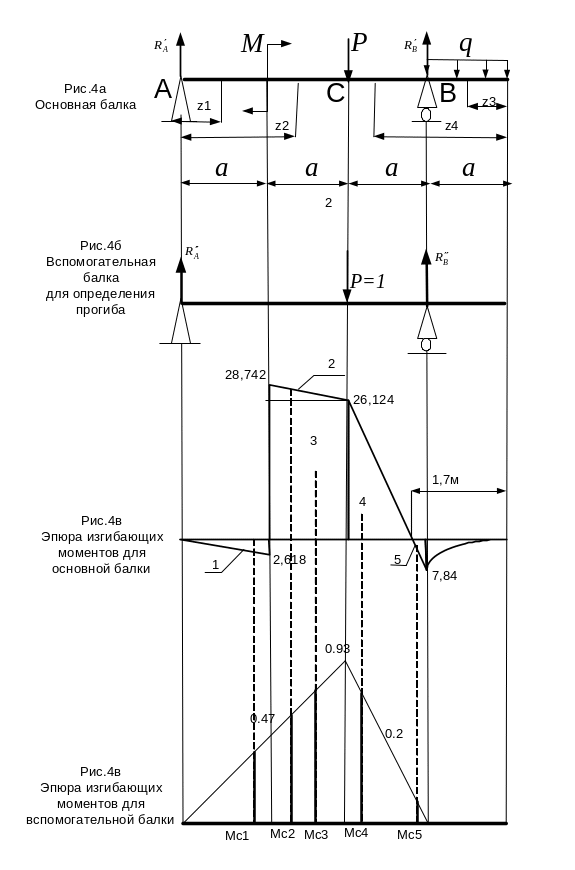
3. Для Ст 20 -модуль упругости

По ГОСТ 8239 - 95 выписываем характеристики двутавра № 10:

, А = 12 , , , , , ,

Тогда жесткость балки равна:

Метод Верещагина

Перемещения по методу Верещагина определяются по формуле:

где ω- площадь эпюры изгибающих моментов для основной балки

Мс-высота (ордината) внутреннего момента под центром тяжести основной балки на единичной эпюре, которую строим для вспомогательной балки.

Определяем площади грузовых эпюр и единичные моменты под центрами тяжести грузовой эпюры (для прогиба в точке С):

1. треугольник: ω=0,5·1,4·2,618=1,8326 = 2/3·0,47=0,31 ω = 0,568

2. треугольник: ω=0,5·1,4(28,742-26,124)=1,8326 =1/3·(,93-0,47)+0,47=0,62 ω =1,142

3. прямоугольник: ω=1,4·26,124=36,573 =0,47+1/2(0,93-0,47)=0,7 ω =25,6

4. треугольник: ω=0,5(2,8-1,7)·26,124=14,368 =0,2+(0,93-0,2) ·2/3 =0,68 ω =9,866

5. треугольник: ω=0,5(1,7-1,4)·7,84=1,176 =2/3·0,2=0,13 ω =0,156

Чтобы определить прогиб в точке С нужно сложить все произведения, рассчитанные по формуле Верещагина и разделить на жесткость балки, в соответствии с правилом знаков треугольник 1и 5 берем со знаком «-» , остальные - со знаком «+»

Задание № 5 тема: устойчивость поперечно сжатых стержней

Дано: Стальной стержень длиной L сжимается силой Р.

Случай А Случай Б

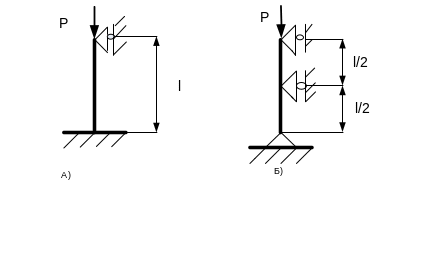
Требуется найти:

1) размеры поперечного сечения при допускаемом напряжении на сжатие

[σ]=240 МПа (расчет производить последовательными приближениями, предварительно задаваясь величиной коэффициента φ = 0,5);

2) величину критической силы и коэффициент запаса устойчивости.

Данные взять из таблицы.

P, kH	l, м	Форма сечения
200	2,7

Случай А)

Р= 200 кН,

l = 2,7 м,

µ = 0,7

σ = 240 МПа

Решение:

1.Находим размеры поперечного сечения

1.1.Выразим площадь сечения через размер «а»

1.2.Определяем моменты инерции сечения относительно главных центральных осей

Для нашего сечения I_мин=I_x=0,1052a⁴

1.3.Выразим минимальный радиус инерции

1.4.Определим гибкость стержня

1.5.Задаемся начальным значением φ, например, φ₁=0,5

1.6.Проектировочный расчет площади:

1.7.Зная площадь, находим размер а :

1.8.Вычисляем гибкость:

j _1табл = 0,45;

j _1табл = 0,52;

j _1табл = 0,52 -

Между j ₁ = 0,5 и j _1табл = 0,45 разница 9,9 %(> 5%), поэтому принимаем второе приближение:

j ₂

1.6.Проектировочный расчет площади:

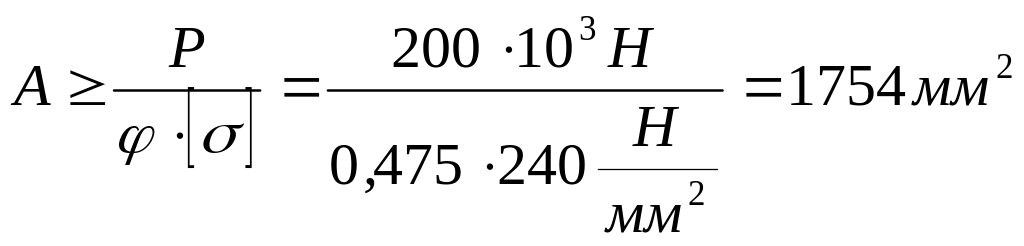
1.7.Зная площадь, находим размер а:

1.8.Вычисляем гибкость:

j _2табл = 0,45;

j _2табл = 0,52;

j _2табл = 0,52 -

Между j ₂ = 0,475 и j _2табл = 0,47 разница 0,6 % (< 5%), поэтому принимаем второе приближение:

a=45,7мм

- поэтому критическую нагрузку определяем по формуле

Эйлера ( - для стальных стержней)

= =

=

Определим коэффициент запаса устойчивости:

Случай Б)

Р= 200 кН,

l = 2,7 м,

µ = 0,5

σ = 240 МПа

Решение:

1.Находим размеры поперечного сечения

1.1.Выразим площадь сечения через размер «а»

1.2.Определяем моменты инерции сечения относительно главных центральных осей

Для нашего сечения I_мин=I_x=0,1052a⁴

1.3.Выразим минимальный радиус инерции

1.4.Определим гибкость стержня

1.5.Задаемся начальным значением φ, например, φ₁=0,5

1.6.Проектировочный расчет площади:

1.7.Зная площадь, находим размер а :

1.8.Вычисляем гибкость:

j _1табл = 0,69;

j _1табл = 0,75

j _1табл = 0,75 -

Между j ₁ = 0,5 и j _1табл = 0,71 разница 30 % (> 5%), поэтому принимаем второе приближение:

j ₂

1.6.Проектировочный расчет площади:

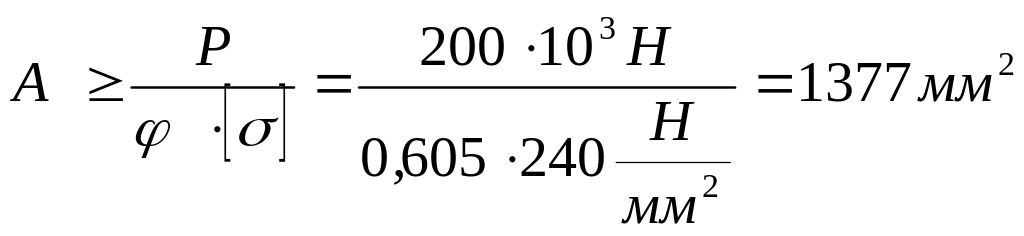
1.7.Зная площадь, находим размер а :

1.8.Вычисляем гибкость:

j _{2 табл} = 0,6;

j _{2 табл} = 0,69;

j _{2 табл} = 0,69-

Между j ₂ = 0,605 и j _{2 табл} = 0,65 разница 7,2 % (> 5% ), поэтому принимаем третье приближение:

j ₃

1.6.Проектировочный расчет площади:

1.7.Зная площадь, находим размер а:

1.8.Вычисляем гибкость:

j _{3 табл} = 0,6;

j _{3 табл} = 0,69;

j _{3 табл} = 0,69-

Между j ₃ = 0,62 и j _{3 табл} = 0,63 разница 2,5 % (< 5% ), поэтому принимаем третье приближение:

a=39,76мм

- поэтому критическую нагрузку определяем по формуле

Ясинского ( - для стальных стержней)

,

где а и в - коэффициенты, МПа;

; ;

А - площадь стального стержня, :

,

Определим коэффициент запаса устойчивости:

Ответ: Случай А: а , , .

Случай Б: а , ; .

Устойчивость сжатого стержня на схеме Б выше т.к. его гибкость меньше, чем у схемы А. Б( )<А( )

Список литературы