Брошюра FLOGOL-2

2. СЕТЕВЫЕ ЯЗЫКИ ФУНКЦИОНАЛЬНОГО И ЛОГИЧЕСКОГО ПРОГРАММИРОВАНИЯ

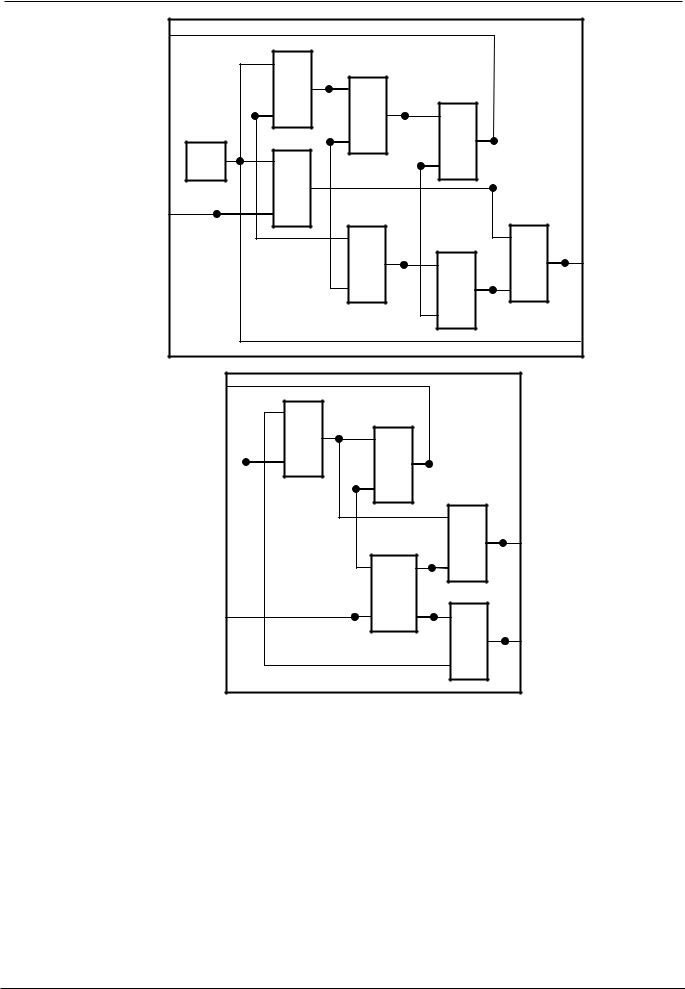
Рис. 2.7. Пример 1.

Рис. 2.8. Пример 2.

Рис. 2.9. Пример 3. Конструктор упорядоченной пары.

FLOGOL: ЯЗЫК И СИСТЕМА ФУНКЦИОНАЛЬНО-ЛОГИЧЕСКОГО ПРОГРАММИРОВАНИЯ 21

2. СЕТЕВЫЕ ЯЗЫКИ ФУНКЦИОНАЛЬНОГО И ЛОГИЧЕСКОГО ПРОГРАММИРОВАНИЯ

Рис. 2.10. Пример 4.

Рис. 2.12. Пример

С

Рис. 2.14. Представление состояний памяти типа «куча».

FLOGOL: ЯЗЫК И СИСТЕМА ФУНКЦИОНАЛЬНО-ЛОГИЧЕСКОГО ПРОГРАММИРОВАНИЯ 22

2. СЕТЕВЫЕ ЯЗЫКИ ФУНКЦИОНАЛЬНОГО И ЛОГИЧЕСКОГО ПРОГРАММИРОВАНИЯ

Рис. 2.13. Пример 7.

FLOGOL: ЯЗЫК И СИСТЕМА ФУНКЦИОНАЛЬНО-ЛОГИЧЕСКОГО ПРОГРАММИРОВАНИЯ 23

2. СЕТЕВЫЕ ЯЗЫКИ ФУНКЦИОНАЛЬНОГО И ЛОГИЧЕСКОГО ПРОГРАММИРОВАНИЯ

Рис. 2.15. Пример 8. Операции с памятью типа «куча».

FLOGOL: ЯЗЫК И СИСТЕМА ФУНКЦИОНАЛЬНО-ЛОГИЧЕСКОГО ПРОГРАММИРОВАНИЯ 24

2. СЕТЕВЫЕ ЯЗЫКИ ФУНКЦИОНАЛЬНОГО И ЛОГИЧЕСКОГО ПРОГРАММИРОВАНИЯ

Рис. 2.16. Пример 9. Операции над памятью типа «куча» в универсуме натуральных чисел.

FLOGOL: ЯЗЫК И СИСТЕМА ФУНКЦИОНАЛЬНО-ЛОГИЧЕСКОГО ПРОГРАММИРОВАНИЯ 25

2. СЕТЕВЫЕ ЯЗЫКИ ФУНКЦИОНАЛЬНОГО И ЛОГИЧЕСКОГО ПРОГРАММИРОВАНИЯ

Рис. 2.16. Пример 9 (продолжение).

2.10. Формализация отношений реляционного включения и эквива-

FLOGOL: ЯЗЫК И СИСТЕМА ФУНКЦИОНАЛЬНО-ЛОГИЧЕСКОГО ПРОГРАММИРОВАНИЯ 26

2. СЕТЕВЫЕ ЯЗЫКИ ФУНКЦИОНАЛЬНОГО И ЛОГИЧЕСКОГО ПРОГРАММИРОВАНИЯ

претации схем d -отношений позволяет раздельно рассмотреть два

существенно более простых исчисления – исчисление сетевой эквивалент-

ности (включения) схем d -отношений и исчисление сильного реляцион-

ного включения сетевых языков. Первое из этих исчислений обозначим

NEC ( Net Equivalence Calculus). В него войдут аксиомы RIC , кроме аксиом

16,17,18,19, и те же правила вывода. Доказательство правильности аксиом,

связанных с константами (остальные, определяющие схемы как множества

сетей, очевидны), легко осуществляется путем рассмотрения r - и n -

представлений схем d -отношений. Например, аксиома RIC

15. ( # ) ( # )

проверяется согласно рис. 2.17 (в центре изображена сеть, представляющая правую и левую части равенства).

Полнота NEC на подмножестве одноэлементных сетевых языков

легко доказывается приведением сетей к каноническому представлению относительно операций последовательной и параллельной композиции с использованием элементарных безэлементных и одноэлементных сетей.

Т е о р е м а 2.9. Две различные связанные основные безэлементные сети одинаковой арности представляют ортогональные d -отношения.

4 Chr(G) – хроматическое число графа G .

FLOGOL: ЯЗЫК И СИСТЕМА ФУНКЦИОНАЛЬНО-ЛОГИЧЕСКОГО ПРОГРАММИРОВАНИЯ 28

2. СЕТЕВЫЕ ЯЗЫКИ ФУНКЦИОНАЛЬНОГО И ЛОГИЧЕСКОГО ПРОГРАММИРОВАНИЯ

связанных переменных, то переменные этих схем одновременно являются

и сортами элементов рассматриваемых сетей.

О п р е д е л е н и е 2.19. Нормализованным представлением конечного множества сетей назовем эквивалентное ему, т.е. имеющее ту же реля-

ционную интерпретацию при любой реляционной интерпретации базиса,

множество связанных сетей (напомним, что, по определению, связанные сети имеют полные dif -графы на множествах точек этих сетей).

Построение нормализованного представления конечного множества сетей иллюстрирует рис. 2.18, на котором показано, как сеть с неполным dif -графом может быть эквивалентно представлена множеством из двух сетей, причем это преобразование может осуществляться до тех пор, пока все сети в рассматриваемом множестве сетей не будут связанными. Ре-

зультативность такого построения очевидна в силу того, что при каждой замене в множестве сети S на пару новых сетей S и S количество

FLOGOL: ЯЗЫК И СИСТЕМА ФУНКЦИОНАЛЬНО-ЛОГИЧЕСКОГО ПРОГРАММИРОВАНИЯ 29

2. СЕТЕВЫЕ ЯЗЫКИ ФУНКЦИОНАЛЬНОГО И ЛОГИЧЕСКОГО ПРОГРАММИРОВАНИЯ

i 1

ставления непосредственно выводится из следствия 1).

FLOGOL: ЯЗЫК И СИСТЕМА ФУНКЦИОНАЛЬНО-ЛОГИЧЕСКОГО ПРОГРАММИРОВАНИЯ 30