УДК 51(076)

ББК 22.1я73 К78

Рецензент доктор физико-математических наук,

профессор кафедры высшей математики

Л. М. Баскин

Рекомендовано к печати редакционно-издательским советом СПбГУТ

Красовская, Т. Ф.

К78 Математика. Операционное исчисление : учебно-методическое пособие по выполнению самостоятельной работы / Т. Ф. Красовская ;

СПбГУТ. – СПб., 2015. – 24 с.

Написано в соответствии с программой учебной дисциплины «Математика», раздел «Операционное исчисление». Приведены основные теоретические сведения, необходимые студентам для освоения методов операционного исчисления для решения линейных дифференциальных уравнений и систем дифференциальных уравнений, а также многих типов интегральных уравнений, рассмотрены особенности применения этих методов. Разобраны решения многих примеров для самостоятельной работы студентов. Приведены вопросы, аналогичные возможным вопросам на экзамене, а также индивидуальные задания для промежуточного контроля знаний по разделу «Операционное исчисление».

Предназначено для студентов всех технических специальностей, изучающих дисциплину «Математика», раздел «Операционное исчисление».

©Красовская Т. Ф., 2015

©Федеральное государственное образовательное бюджетное учреждение высшего профессионального образования «Санкт-Петербургский государственный университет телекоммуникаций им. проф. М. А. Бонч-Бруевича», 2015

2

3

ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ. ТЕОРЕМЫ СУЩЕСТВОВАНИЯ И ЕДИНСТВЕННОСТИ

Основой операционного исчисления служит введение так называемого преобразования Лапласа.

Определение. Преобразованием Лапласа функции f(t) называется

F(p) = L {f(t), p} = ∫ dt.

Преобразование Лапласа характерно тем, что многим операциям и соотношениям над f(t) соответствуют более простые соотношения и операции над F(p). Поэтому найти F(p) часто удается гораздо проще, чем f(t) и в дальнейшем вопрос состоит в том, как по F(p) восстановить f(t), что, как правило, легче, чем непосредственно искать (t).

Очевидно, что F(p) – это несобственный интеграл, зависящий от параметра р (р – это комплексная переменная), поэтому важен вопрос, когда этот интеграл сходится, т. е. когда F(p) существует. Ответ на этот вопрос дает теорема существования.

Теорема существования. Пусть (t) – есть так называемая функцияоригинал, т. е. она удовлетворяет следующим трем условиям:

1) при t 0 f(t) 0;

2) f(t) – кусочно-непрерывная функция, т. е. на любом конечном отрезке она или непрерывна, или может иметь конечное число разрывов первого рода на этом отрезке;

3) существуют числа М 0 и р0 0 такие, что выполняется неравенство | | M , что означает, что функция f(t) ограничена в своем росте некоторой экспонентой, при этом число р0 называется показателем ро-

В случае выполнения условий теоремы, т. е., когда f(t) есть оригинал, F(p) называют изображением и связь между f(t) и F(p) символически записывают так: f(t) F(p).

Также полезно сформулировать еще одну теорему.

Теорема единственности. Если две непрерывные функции f(t) и g(t) имеют одно и то же изображение F(p),то f(t) g(t).

Из этих двух теорем вытекает, что соответствие f(t) F(p) по существу взаимно-однозначно для большинства практических целей и часто определяется просто по составленным специальным таблицам.

Связь между преобразованием Лапласа и прямым преобразованием Фурье

Напомним, что прямое преобразование Фурье функции f(t) имеет вид:

4

Сделаем замену во втором интеграле t = –z:

т. е. прямое преобразование Фурье линейно связано с преобразованием Лапласа и поэтому их свойства во многом одинаковы. Однако, в отличие от преобразования Лапласа, преобразование Фурье годится также и для задач, где f(t) определено не тождественным нулем и при t 0.

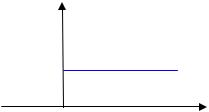
Единичная функция Хэвисайда. Ее изображение

1,t 0 η(t) 0,t 0

Ее график представлен на рис. 1.

η(t)

1

При отыскании изображения функция-оригинал по теореме существования при t 0 тождественно равна 0. Таким образом, рассматривая обычные функции математического анализа, мы на самом деле подразумеваем, что эти функции при t 0 тождественно равны 0. Это можно записывать, как произведение соответствующей функции на (t), т. е. если мы пишем в качестве

ный ноль. Поэтому, если мы в дальнейшем пишем 1 в качестве функции-

5

СВОЙСТВА ПРЕОБРАЗОВАНИЯ ЛАПЛАСА

Расширить таблицу изображений элементарных функций нам помогут следующие свойства преобразования Лапласа.

Доказательство очевидно в силу линейности оператора интегрирования, так как преобразование Лапласа по сути своей есть именно интеграл.

Делаем замену z = at; dz = adt.

Расширим еще таблицу изображений:

Пример 3.

Найти изображение для данного оригинала:

6

Пример 4.

Найти по данному изображению оригинал:

нале, в частности и в (t), которая (может быть, и неявно) всегда входит в функцию-оригинал. Таким образом, при запаздывании оригинал слева от тождественно равен 0, так как функция Хэвисайда с запаздыванием на

что и требовалось доказать.

Пример 5. Восстановить оригинал по изображению:

.

Замечание 1. Если в составе оригинала нет функции Хэвисайда с запаздыванием, то это означает, что в оригинале нет запаздывания. Например, если надо найти изображение функции f(t) = cos5(t – 3), то здесь нельзя применить теорему запаздывания. Получаем:

Замечание 2. Функция Хэвисайда с запаздыванием очень удобна, если мы хотим записать одним выражением так называемую «составную» функцию, т. е. функцию, которая задается разными выражениями на разных участках числовой оси, с тем, чтобы в дальнейшем найти ее изображение, используя теорему запаздывания.

Пример 6. Найти изображение функции f(t), заданной следующим образом:

{

7

Интеграл справа – это двукратный повторный интеграл по области, ограниченной прямыми = 0; = t, причем 0 . Изменим порядок интегрирования, тогда пределы внутреннего интегрирования по t будут:

что и требовалось доказать.

Пример 8. Записать свертку функций f(t) = sin 3t и g(t) = cos 2t и найти изображение этой свертки:

ТЕОРЕМА О ДИФФЕРЕНЦИРОВАНИИ ИЗОБРАЖЕНИЯ

что и требовалось доказать.

Следствие. Теперь можно вывести изображение степенной функции:

. . . . . . . . . . . . .

9