Глава 3
Теория функций комплексной переменной,
Операционное исчисление,
Теория вероятностей
§ 1. Теория функций комплексной переменной
Рассматриваются следующие задачи: действия с комплексными числами; решение уравнений с комплексной переменной; интегрирование функции комплексной переменной.
Задача
77. Представить
в тригонометрической и показательной
форме число
.
Решение. Число задано в алгебраической форме и в общем случае имеет вид
.
Здесь х и у – соответственно действительная и мнимая части комплексного числа z, а i – мнимая единица (i2 = −1).
Число z изображается на комплексной плоскости точкой с координатами х и у (рис. 7).
Рис.7
Алгебраическая, тригонометрическая и показательная формы связаны соотношениями
,
где
– модуль комплексного числа z
(радиус-вектор, соединяющий начало
координат с точкой z);
– аргумент комплексного числа z
(угол между осью Ох
и радиус-вектором
).
При этом
,
.
С другой стороны,
,
.
В
силу многозначности
будем рассматривать только его главное
значение из промежутка
,
используя соотношение
.
Для
имеем
,
,
поэтому
.
Так как
и число z расположено во второй четверти (рис. 8), получим
.
Тогда
.
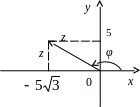
Рис. 8
Задача
78. Представить
в тригонометрической и показательной
форме число
.
Решение.
Здесь х
= 0, у
= −2 (см. задачу 77), поэтому
.
Построив
(рис. 9), определим
(формула
неприменима, так как х
= 0).
Рис. 9
Итак,
.
Задача
79. Вычислить
.
Решение.
Выполнить
действия с комплексными числами −
значит представить результат в
алгебраической, тригонометрической
или показательной формах (см. задачу
77). В данном случае получим алгебраическую
форму вида
,
для чего умножим числитель и знаменатель
дроби на комплексно сопряженное к
знаменателю число (
).
В результате получим
.
Задача
80. Вычислить
.
Решение. Возвести комплексное z число в степень n можно по формуле Муавра
,
где и − соответственно модуль и аргумент комплексного числа z.
Найдем
и
(см. задачу 77). Так как х
= 1,
,
получим
.
Поскольку число z расположено в четвертой четверти (рис. 10), имеем
.
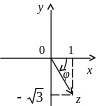
Рис. 10
Тогда
Задача
81. Решить
уравнение
.
Решение. Преобразуем уравнение к виду
.
Тогда
и, значит, следует применить формулу Муавра извлечения корня степени n из комплексного числа
.
Здесь и − соответственно модуль и аргумент подкоренного выражения z.
Находим
и
для числа
(см. задачу 77):
.
Так как число w расположено в третьей четверти (рис. 11), то
.
Рис. 11
Далее получаем
Задача
82. Вычислить
.
Решение.
Поскольку i
− число (
),
а
,
имеем
.
§ 2. Операционное исчисление
Рассматриваются задачи: нахождение изображения по заданному оригиналу; нахождение оригинала по заданному изображению, нахождение изображения свертки с применением теоремы Бореля; решение дифференциальных уравнений операционным методом.
Задача 83. Найти изображение F(p) для функции-оригинала
.
Решение. Функция-оригинал f(t) и ее изображение F(p) связаны соотношением
(или
коротко:
).
Применение этого равенства приводит к известным формулам изображений элементарных функций, согласно которым
,
,
,
,
,
.
Замечание.
На самом деле здесь перечислены
изображения элементарных функций,
умноженных на единичную функцию Хевисайда
,
которую обычно не пишут. Сама же функция
Хевисайда имеет изображение
.
Так как изображение суммы оригиналов равно сумме изображений, получаем
.
Задача 84. Найти изображение F(p) для функции-оригинала
.
Решение. Преобразуем f(t) с помощью формул элементарной математики [приложение 5]:
,
,
,
,
.
В результате получим
.
Теперь можно применить формулы изображений элементарных функций [приложение 6]. Имеем
.
Задача 85. Найти функцию-оригинал f(t) по заданному изображению
.
Решение. Воспользуемся формулами связи функций-оригиналов и их изображений [приложение 6]. Получим
,
,
,
,
.
Окончательно имеем
.
Задача 86. Найти изображение свертки функций:
1)
;
2)
;
3)
.
Решение.
Согласно теореме Бореля свертка
(обозначается
)
функций f(t)
g(t)
имеет изображением функцию F(p)·G(p)
(здесь
,
).
Значит, для получения искомого изображения
достаточно перемножить изображения
каждой из свертываемых функций. Используя
формулы изображений элементарных
функций [приложение 6], получим
1)
;
2)
;
3)
.
Задача 87. Средствами операционного исчисления решить дифференциальное уравнение
.
Решение. Считая искомую функцию y(t) функцией-оригиналом, обозначим ее изображение Y(p) и найдем изображения левой и правой частей дифференциального уравнения. Согласно формуле дифференцирования оригинала
и с учетом нулевых начальных условий получим
,
.
Так
как
[приложение
6], для правой части имеем
.
В результате дифференциальное уравнение, записанное в изображениях, примет вид
.
Решаем
его относительно
:
,
т.е.
.
Возвращаясь от изображения Y(p) к оригиналу y(t), получим искомое решение дифференциального уравнения
.